湘教版七年级下册2.2.2完全平方公式精练

这是一份湘教版七年级下册2.2.2完全平方公式精练，共38页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
1.(2023八上·重庆月考）如图所示的四边形均为矩形或正方形，下列等式能够正确表示该图形面积关系的是（ ）
A. (a+b)2=a2+2ab+b2 B. (a+b)2=a2+2ab-b2
C. (a-b)2=a2-2ab+b2 D. (a-b)2=a2-2ab-b2
2.(2023八上·唐河期中）如图，将图1中的阴影部分拼成图2，根据两个图形中阴影部分的关系，可以验证下列哪个计算公式( )
A. a2−b2=(a+b)(a−b) B. (a−b)2=a2−2ab+b2
C. (a−b)2=a2+2ab+b2 D. (a+b)2=(a−b)2+4ab
3.(2023八上·哈尔滨月考）如图所示的四边形均为矩形或正方形，下列等式能够符合题意表示该图形面积关系的是（ ）
A. (a+b)(a-b)=a2+b2 B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. (a-b)2=a2-2ab-b2
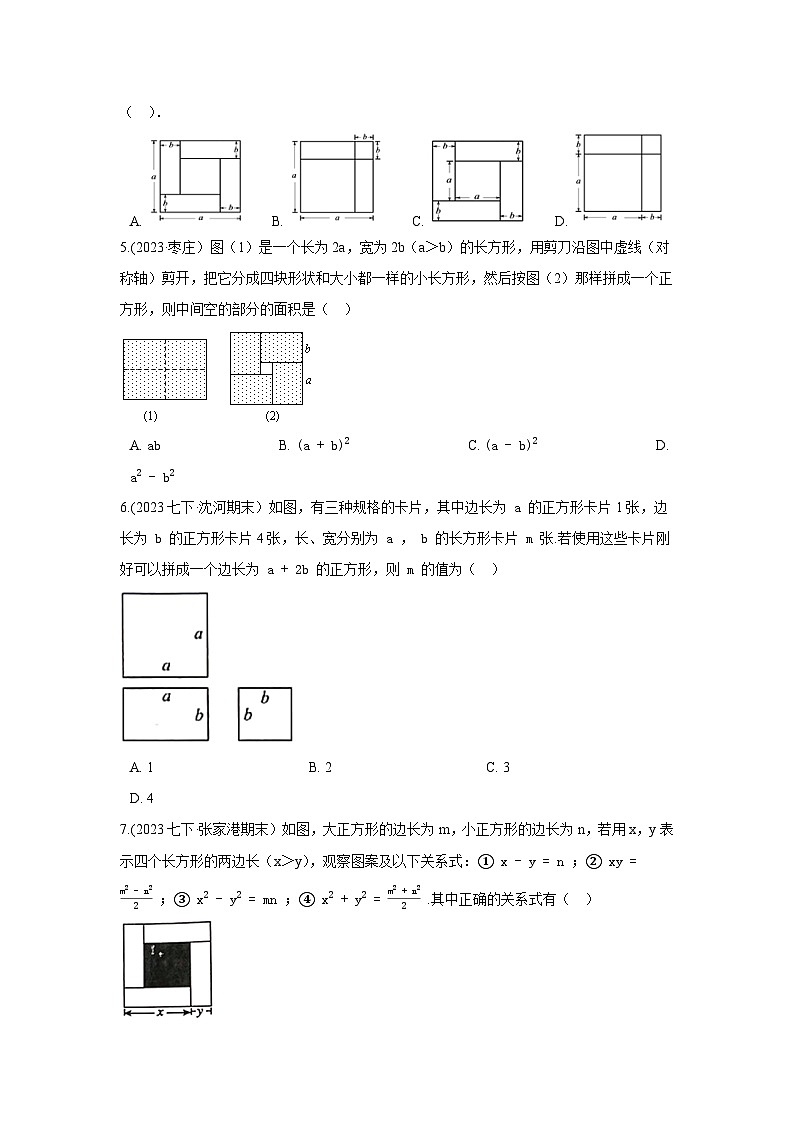
4.下列各图是由若干个正方形和长方形组成的，其中能表示等式(a+b)2=a2+2ab+b2的是（ ）．
A. B. C. D.
5.(2023·枣庄）图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ）
A. ab B. (a+b)2 C. (a-b)2 D. a2-b2
6.(2023七下·沈河期末）如图，有三种规格的卡片，其中边长为 a 的正方形卡片1张，边长为 b 的正方形卡片4张，长、宽分别为 a ， b 的长方形卡片 m 张.若使用这些卡片刚好可以拼成一个边长为 a+2b 的正方形，则 m 的值为（ ）
A. 1 B. 2 C. 3 D. 4
7.(2023七下·张家港期末）如图，大正方形的边长为m，小正方形的边长为n，若用x，y表示四个长方形的两边长（x＞y），观察图案及以下关系式：① x-y=n ；② xy=m2-n22 ；③ x2-y2=mn ；④ x2+y2=m2+n22 .其中正确的关系式有（ ）
A. ①② B. ①③ C. ①③④ D. ①②③④
8.(2023七下·余杭期末）小方将4张长为a、宽为b（a>b）的长方形纸片先按图1所示方式拼成一个边长为（a+b）的正方形，然后按图2所示连接了四条线段，并画出部分阴影图形，若大正方形的面积是图中阴影部分图形面积的3倍，则a、b满足（ ）
A. a=3b B. 2a=5b C. a=2b D. 2a=3b
9.(2023七下·南岸期末）如图，在边长为a+b的正方形的四个角上，分别剪去直角边长分别为 a , b 的四个直角三角形，则剩余部分面积，即图中的阴影部分的面积是（ ）
A. a2-b2 B. 2ab C. a2+b2 D. 4ab
10.(2023七下·郏县期末）通过计算几何图形的面积可表示一些代数恒等式，小明从图中得到 4 个代数恒等式：① x(x+y)=x2+xy ；② x2+3xy+2y2=(x+y)(x+2y) ；③ (x+2y)2=x2+4xy+4y2 ；④ x2+2xy+y2=(x+y)2 其中正确的有（ ）
A. ②③ B. ①②③ C. ①②④ D. ①②③④
11.(2023七下·瑞安期末）如图,正方形ABCD和长方形DEFG的面积相等,且四边形AEFH也为正方形.欧几里得在《几何原本》中利用该图得到了:AH2=AB×BH.设AB=a，BH=b.若ab=45，则图中阴影部分的周长为（ ）
A. 25 B. 26 C. 28 D. 30
12.(2023七下·郑州期末）如图，有两个正方形A,B,现将B放在A的内部得图甲，将A,B并列放置后构造新的正方形得图乙。若图甲和图乙中阴影部分的面积分别为3和30,则正方形A、B的面积之和为( )

A. 33 B. 30 C. 27 D. 24
13.(2023七下·合肥月考）如图，正方形卡片 A 类， B 类和长方形卡片 C 类若干张，如果要用 A 、 B 、 C 三类卡片拼一个边长为 (a+2b) 的正方形，则需要 C 类卡片的张数是（ ）．

A. 2 B. 3 C. 4 D. 6
14.(2023八下·涡阳月考）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由三角形较长直角边长为a，较短直角边长为b，若（a＋b）2＝21，大正方形的面积为13，则小正方形的面积为（ ）
A. 3 B. 4 C. 5 D. 6
15.(2023七下·泗辖期中）我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图①可以用来解释(a＋b)2－(a－b)2＝4ab.那么通过图②中阴影部分面积的计算验证了一个恒等式，此等式是( )
A. a2－b2＝(a＋b)(a－b) B. (a－b)2＝a2－2ab＋b2
C. (a＋b)2＝a2＋2ab＋b2 D. (a－b)(a＋2b)＝a2＋ab－b2
16.(2023七下·龙岗期中）如图，两个正方形边长分别为a、b ， 如果a+b=9，ab=12，则阴影部分的面积为（ ）

A. 25 B. 22.5 C. 13 D. 6.5
17.(2023七下·新昌期中）如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形中阴影
部分面积的关系，可以直观地得到一个关于a，b的恒等式为（ ）
A. a2－b2＝（a＋b）（a－b） B. （a＋b）2＝a2＋2ab＋b2
C. （a－b）2＝（a＋b）2－4ab D. a2＋ab＝a（a＋b）
18.(2023七下·滨湖期中）有一张边长为 a 的正方形桌面，因实际需要，需将正方形边长增加 b ，木工师傅设计了如图际所示的方案，该方案能验证的等式是（ ）
A. (a+b)2=a2+2ab+b2 B. a2-b2=(a+b)(a-b)
C. (a-b)2=a2-2ab+b2 D. (a+2b)(a-b)=a2+ab+b2
19.(2023七下·杭州期中）有两个正方形A，B，现将B放在A的内部如图甲，将A，B并排放置后构造新的正方形如图乙。若图甲和图乙中阴影部分的面积分别为 14 和 134 ，则正方形A，B的面积之和为( )

A. 3 B. 3.5 C. 4 D. 4.5
20.(2023九上·灌云月考）如图是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ）
A. a2+b2 B. 4ab C. （b+a）2﹣4ab D. b2﹣a2
二、填空题
21.(2023七下·嘉兴期末）如图，在长方形ABCD中，AB