湘教版（2024）八年级上册5.1 二次根式精品教案

这是一份湘教版（2024）八年级上册5.1 二次根式精品教案，共5页。

课题
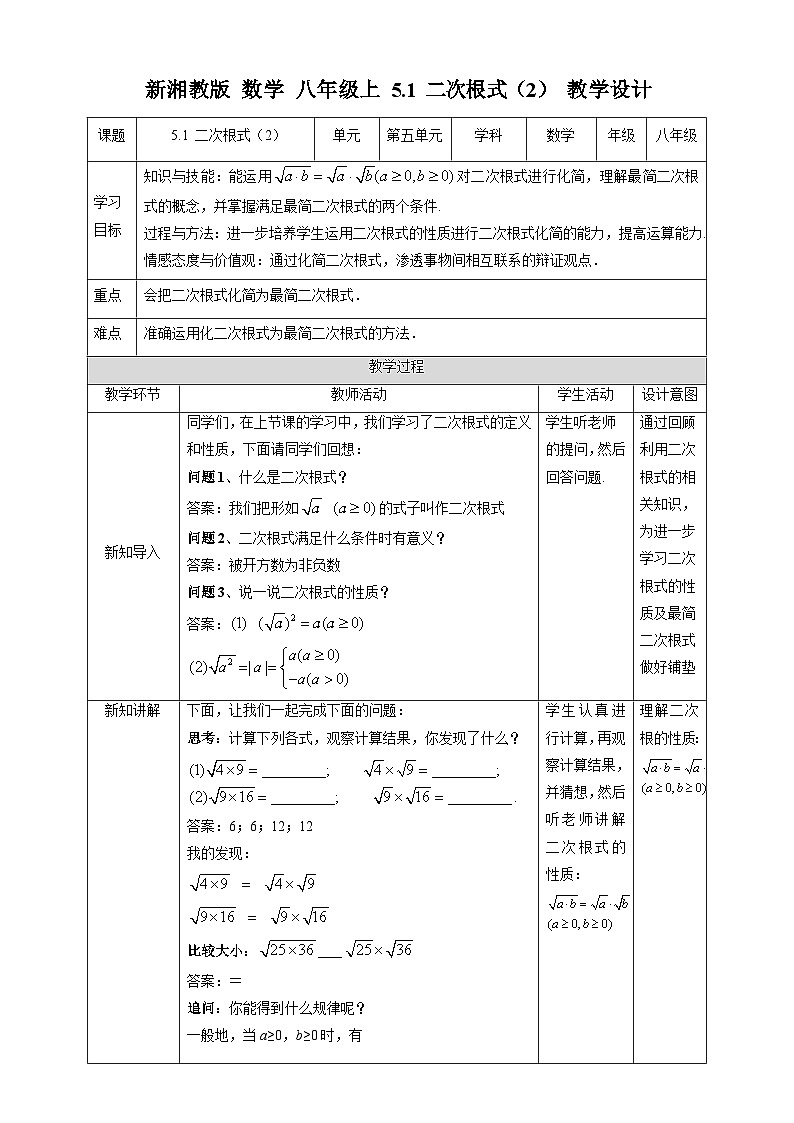
5.1 二次根式（2）
单元
第五单元
学科
数学
年级
八年级
学习
目标
知识与技能：能运用对二次根式进行化简，理解最简二次根式的概念，并掌握满足最简二次根式的两个条件.
过程与方法：进一步培养学生运用二次根式的性质进行二次根式化简的能力，提高运算能力.
情感态度与价值观：通过化简二次根式，渗透事物间相互联系的辩证观点．
重点
会把二次根式化简为最简二次根式．
难点
准确运用化二次根式为最简二次根式的方法．
教学过程
教学环节
教师活动
学生活动
设计意图
新知导入
同学们，在上节课的学习中，我们学习了二次根式的定义和性质，下面请同学们回想：
问题1、什么是二次根式？
答案：我们把形如的式子叫作二次根式
问题2、二次根式满足什么条件时有意义？
答案：被开方数为非负数
问题3、说一说二次根式的性质？
答案：
学生听老师的提问，然后回答问题.
通过回顾利用二次根式的相关知识，为进一步学习二次根式的性质及最简二次根式做好铺垫
新知讲解
下面，让我们一起完成下面的问题：
思考：计算下列各式，观察计算结果，你发现了什么？
答案：6；6；12；12
我的发现：
比较大小：
答案：＝
追问：你能得到什么规律呢？
一般地，当a≥0，b≥0时，有
因此
即：
例1：化简下列二次根式.
解：
练习1：化简下列二次根式.
解：
例2：化简下列二次根式.
解：
注意：化简二次根式时，最后结果要求被开方数不含分母.
练习2：化简下列二次根式.
解：
归纳：二次根式化简后的结果，具有以下特点：
（1） 被开方数中不含开得尽方的因数（或因式）；
（2） 被开方数不含分母.
我们把满足上述两个条件的二次根式，叫作最简二次根式.
注意：在二次根式的运算中，一般要把最后结果化为最简二次根式.
练习3：下列根式中是最简二次根式的是( )
答案：B
学生认真进行计算，再观察计算结果，并猜想，然后听老师讲解二次根式的性质：
学生认真完成例1、例2及练习题，在计算的过程中体会二次根式的化简.
学生仔细观察例题与练习题的结果，在老师的讲解下理解最简二次根式的定义.
理解二次根的性质：
引导学生运用
对二次根式进行化简
提高学生对一元一次不等式组的求解能力.
理解最简二次根式的概念，并会判断一个二次根式是否属于最简二次根式
课堂练习
下面请同学生独立完成课堂练习.
1．若eq \r(9－a2)＝eq \r(3－a)·eq \r(3＋a)成立，则a的取值范围是( )
A．－3≤a≤3 B．a＞－3 C．a＜3 D．－3＜a＜3
答案：A
2．下列二次根式中，不能化简成为aeq \r(2)(a为有理数)形式的是( )
A.eq \r(98) B．eq \r(72) C．eq \r(48) D．eq \r(50)
答案：C
3．下列式子中，属于最简二次根式的是( )
A.eq \r(9) B．eq \r(7) C.eq \r(20) D．eq \r(－23)
答案：B
4．下列等式成立的是( )
A.eq \r(4＋9)＝eq \r(4)＋eq \r(9)
B.eq \r(－33)＝－3eq \r(－3)
C.eq \r(－2×－3)＝eq \r(－2)×eq \r(－3)
D.eq \r(125)＝5eq \r(5)
答案：D
5．化简：
(1)eq \r(1\f(4,5))； (2)eq \r(－16×－72×63)；
(4)eq \r(32＋62)； (4)aeq \r(\f(1,8a)).
解：(1)eq \f(3,5)eq \r(5) (2)72eq \r(14) (3)3eq \r(5) (4)eq \f(\r(2a),4)
6．交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v＝16eq \r(df)，其中v表示车速(单位：千米/时)，d表示刹车后车轮滑过的距离(单位：米)，f表示摩擦系数．在某次交通事故调查中，测得d＝20米，f＝1.2.则肇事汽车的车速大约是多少？(eq \r(6)取2.449，结果精确到0.01千米/时)
解：当d＝20，f＝1.2时，
v＝16×eq \r(20×1.2)＝32eq \r(6)≈78.37(km/h)．
学生自主完成课堂练习，做完之后班级内交流.
借助练习，检测学生的知识掌握程度，同时便于学生巩固知识.
拓展提高
我们一起完成下面的问题：
化简：
分析：由eq \r(－\f(1,a))有意义；可得－eq \f(1,a)＞0，即a＜0，因此eq \r(a2)＝－a.
解：原式＝aeq \r(\f(－a,a2))＝a·eq \f(\r(－a),\r(a2))＝a·eq \f(\r(－a),－a)＝－eq \r(－a).
在师的引导下完成问题.
提高学生对知识的应用能力
课堂总结
在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：
1、如何利用积的算术平方根的性质化简二次根式？
答案：
2、满足最简二次根式的条件有哪些？
答案：（1） 被开方数中不含开得尽方的因数（或因式）；
（2） 被开方数不含分母.
跟着老师回忆知识，并记忆本节课的知识.
帮助学生加强记忆知识.
作业布置
基础作业
教材第160页习题5.1A组第4、5、6题
能力作业
教材第160页习题5.1B组第8题
学生课下独立完成.
检测课上学习效果.
板书设计
课题：5.1 二次根式（2）
教师板演区
学生展示区
1.二次根式的化简
2.最简二次根式；
借助板书，让学生知道本节课的重点。