人教版五年级数学上册第六单元表集体备课教案例3、例4和例5

学科

数学

年级

五年级

备课

教师

课时安排

 1 课时

课题  多边形的面积—梯形的面积

学习目标1.在平行四边形、三角形的面积计算公式推导的基础上，概括出梯形面积计算公式。正确、较熟练地运用公式计算梯形面积，2.渗透数学迁移、转化思想，让学生感受数学与生活的紧密联系．提高学生学习数学的兴趣。

达成评价

1借助平行四边形、三角形的面积计算公式推导的基础上，概括出梯形面积计算公式2能够应用梯形公式正确计算梯形的面积

先行组织：信息中提到三峡水电站大坝的一部分是梯形,怎样求梯形的面积?

新知建构

 生活中的图形除了三角形和平行四边形外，还有梯形，这节课我们就利用转化的方法来研究梯形的面积计算公式。

任务一：梯形面积公式的推导

活动1（1）利用割法补推导。把梯形分割成两个三角形

（2）利用拼摆法推导。把两个完全一样的梯形拼成一个平行四边形小组活动，

活动2教师深入各小组进行指导。可提醒学生用剪刀剪一剪，再拼一拼。交流汇报自己的推导过程。

（1）把一个梯形剪成两个三角形。

梯形的面积＝三角形1的面积+三角形2的面积＝梯形上底×高÷2+梯形下底×高÷2＝（梯形上底+梯形下底）×高÷2

（2）用两个一样的梯形拼成一个平行四边形，这个平行四边形的底等于梯形的（上底+下底），这个平行四边形的高等于梯形的高。每个梯形的面积等于拼成的平行四边形面积的一半，所以梯形的面积＝（上底+下底）×高÷2。

任务二：梯形面积计算

活动（1）出示教材第94页例3情境图和横截面的示意图，引导学生观察情境图并思考：横截面是一个什么形状？让学生找一找，直角梯形的高在哪里？你能理解这个横截面的含义吗？

嵌入评价（1）小组合作交流，分享梯形面积公式的推导过程

（2）归纳出梯形的面积＝（上底+下底）×高÷2。高

能正确应用梯形的面积公式计算面积

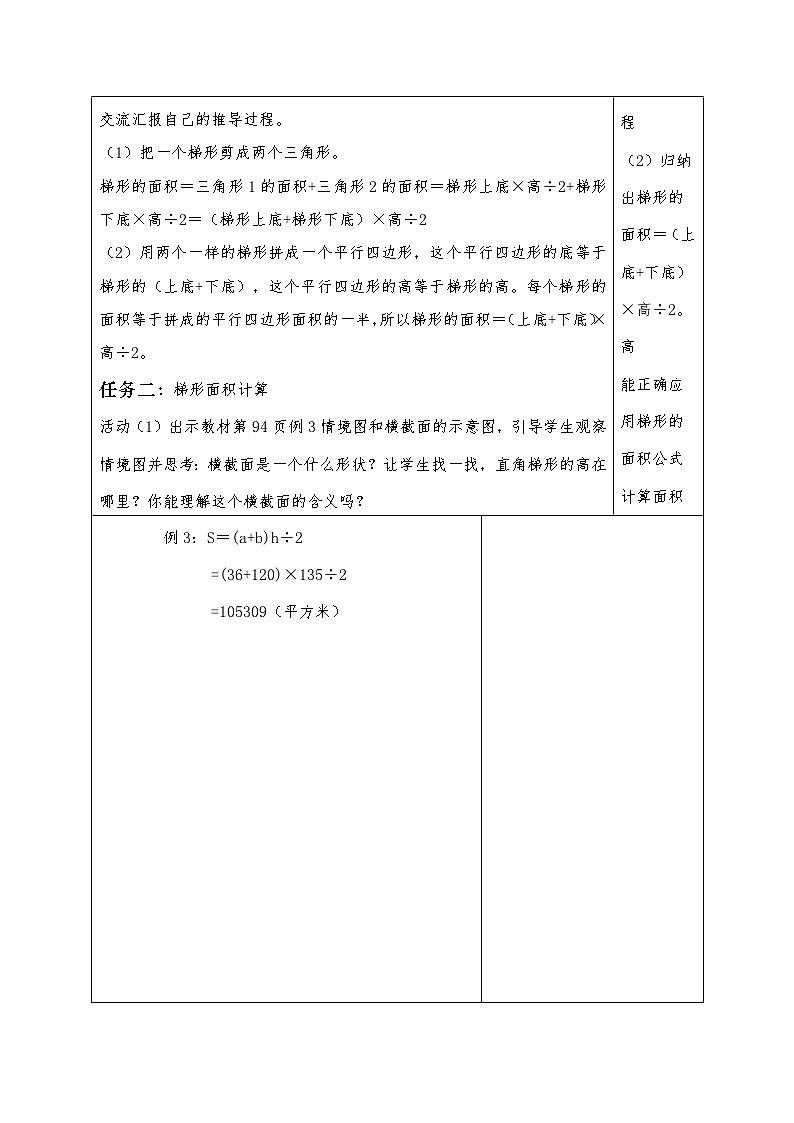
例3：S＝(a+b)h÷2

              =(36+120)×135÷2

=105309（平方米）

迁移运用：完成教材第96页“做一做”。

成果集成：   梯形的面积

梯形的面积=（上底+下底）×高÷2

用字母表示：S=(a+b)×h÷2

例3：S＝(a+b)h÷2

                   =(36+120)×135÷2

                   =105309（平方米）

作业设计：

完成教材第95页“练习二十一”第2、3、4题。

学科

数学

年级

五年级

备课

教师

课时安排

 1 课时

课题组合图形的面积（1）

学习目标

1.结合生活实际认识组合图形，并掌握用分解法或添补法求组合图形的面积。

2.根据各种组合图形的自身条件，选择有效的计算方法进行面积计算。

3.能运用组合图形的知识，解决生活中组合图形的实际问题。

达成评价

（1）掌握用分解法或添补法求组合图形的面积。（2）选择有效的计算方法进行面积计算。（3）能正确解决生活中组合图形的实际问题。

先行组织：前面我们会计算平行四边形、三角形、梯形等图形的面积，那么组合图形的面积怎样计算呢？

新知建构

问题与活动（做什么、怎么做）

嵌入评价（做到什么程度）

（1）学生能正确知道组合图形是由哪些简单的图形组成，相同的图形有不同的组合方法

（2）能正确计算组合图形的面积

迁移运用：完成教材第99页“练习二十二”第1题

成果集成： 组合图形的面积（1）

由两个或两个以上的简单图形组成的大的不规则图形叫组合图形。

    5×5+5×2÷2     (5+5+2)×(5÷2)÷2×2

＝25+5            =12×2.5÷2×2

＝30(m2)           =30 (m2)

作业设计：教材第99页练习二十二第4、5、6题

学科

数学

年级

五年级

备课

教师

课时安排

 1 课时

课题  方格图中不规则图形的面积计算

学习目标

1.初步掌握“通过将不规则图形近似地看作可求面积的多边形来求图形的面积”。

2.用数格子方法和近似图形求积法估测不规则图形的面积。

达成评价

 1.掌握通过将不规则图形近似地看作可求面积的多边形来求图形的面积”。

2.会应用用数格子方法和近似图形求积法估测不规则图形的面积。

先行组织： 组合图形的面积会计算了，那么怎样用数格子方法和近似图形求积法估测不规则图形的面积？

新知建构

问题与活动（做什么、怎么做）

嵌入评价（做到什么程度）

  出示一片树叶，先让学生指一指树叶的面积是哪一部分？指名几名学生上台指一指。

引导学生思考：它是一个不规则的图形，那么面积如何计算呢？

 任务一：出示教材第98页情境图中的树叶。

活动1 引导思考：这片叶子的形状不规则，怎么计算面积呢？

让学生思考，并在小组内交流。

学生可能会想到：可以将树叶放在透明方格纸上来计数。

对学生的回答要给予肯定，并强调还是要用一个统一的标准的方格进行计数。

演示教材第98页情境全图：在树叶上摆放透明的每格1平方厘米方格纸。

引导学生观察情境图，说一说发现了一些什么情况？

学生可能会看出：树叶有的在透明的厘米方格纸中，出现了满格、半格，还出现了大于半格和小于半格的情况

 活动2自主探索树叶的面积

明确：为了计算方便，要先在方格纸上描出叶子的轮廓图。

 提示：如果把不满一格的都按半格计算，这片叶子的面积大约是多少平方厘米？

学生通过数方格可以得出：这片叶子的面积大约是27cm2。

质疑：为什么这里要说树叶的面积是“大约”？

学生自主回答：因为有的多算，有的不算，算出的面积不是准确数。

3．让学生拿出树叶及小方格纸，以小组为单位研究树叶面积的计算。

 4．引导：你还能用其他方法来计算叶子的面积吗？

 思考：你能将叶子的图形近似转化成平行四边形吗？

学生回答，师根据学生的回答多媒体出示将叶子转化成平行四边形的过程（即教材第100页第三幅情境图）。

再让学生数一数这个平行四边形的底与高分别是多少，再尝试计算。

（平行四边形的底是5厘米，高6厘米。）

学生自主解答，并汇报。

根据学生汇报板书计算过程：

    S＝ah

     ＝5×6

     ＝30(cm2)

5．让学生再说一说，你是怎样估算树叶的面积？

（1）先让学生估一估，这片叶子的面积大约是多少平方厘米。

通过讨论，学生可能会想到：可以把少的与多的拼在一起算一格；也可以把大于等于半格的算一格，小于半格的可以舍去不算。

（2）能正确用数格子方法和近似图形求积法估测不规则图形的面积。

迁移运用：完成教材第100页“练习二十二”第8题。

成果集成： 方格图中不规则图形的面积计算

先通过数方格确定面积的范围，

再把不规则图形转化为学过的图形来估算。

  S＝ah

   ＝5×6

                 ＝30(cm2)

作业设计：教材第100页练习二十二第7、11题