第一章特殊平行四边形复习与小结-（北师大）课件PPT

这是一份第一章特殊平行四边形复习与小结-（北师大）课件PPT，共16页。
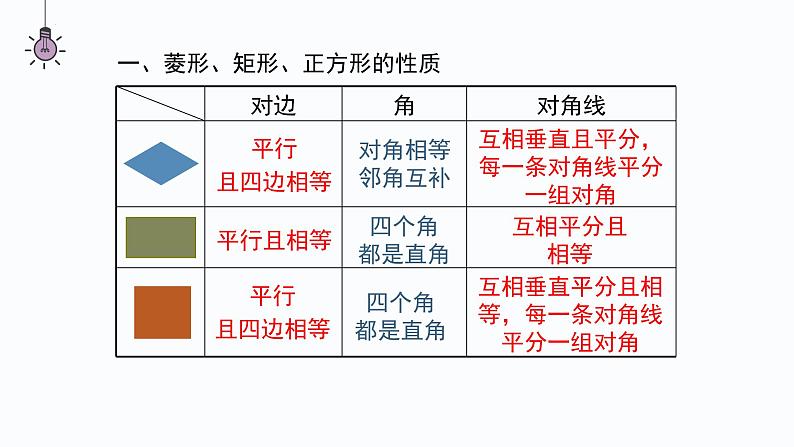
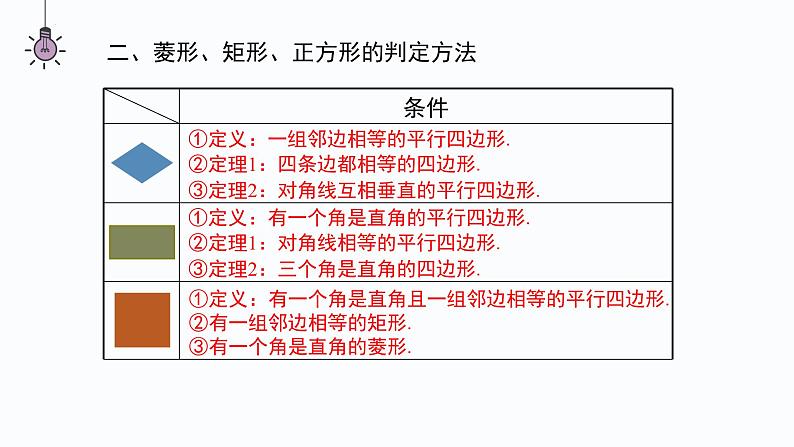
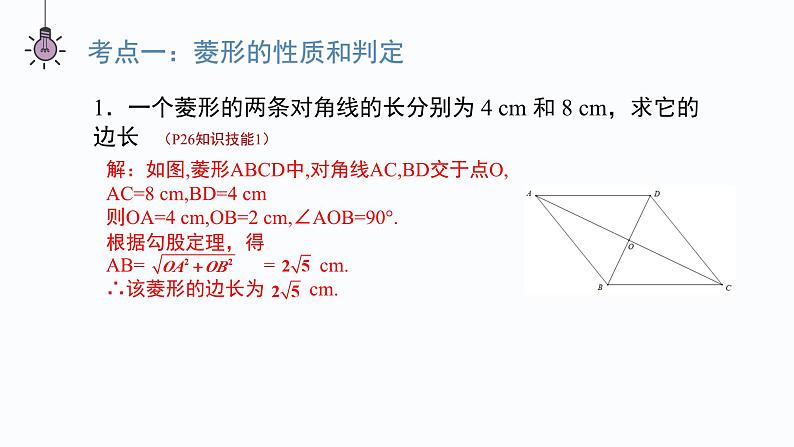
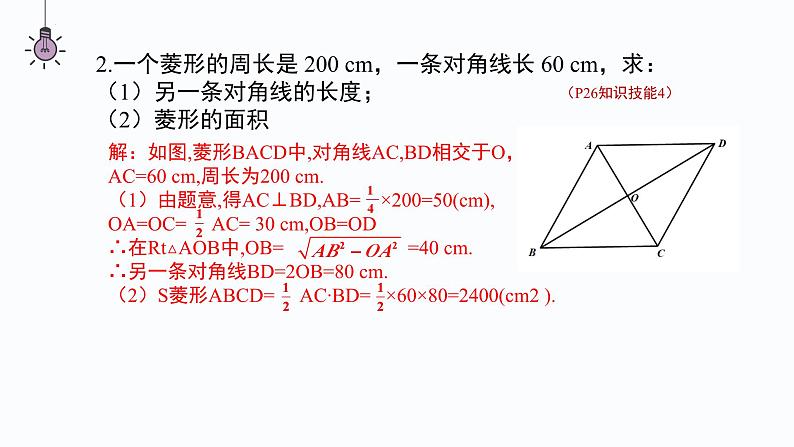
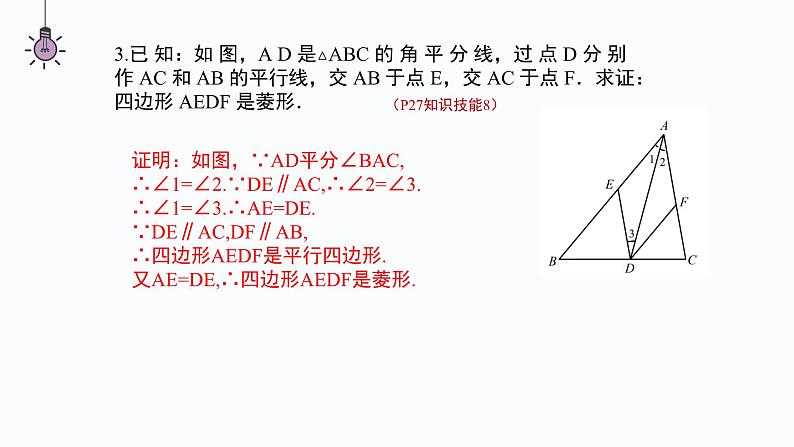
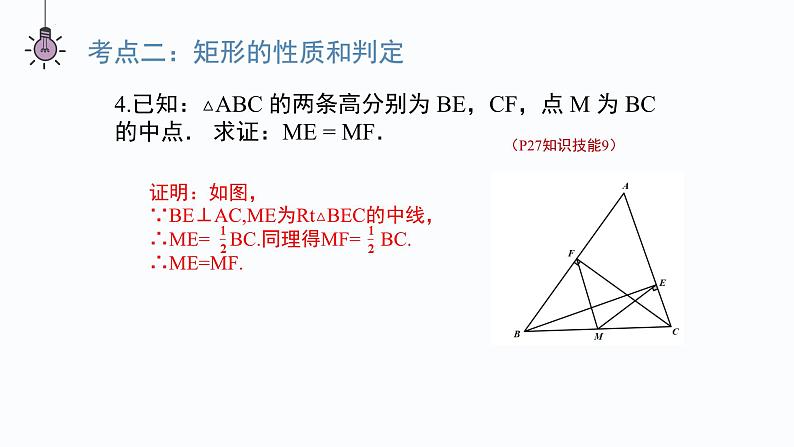
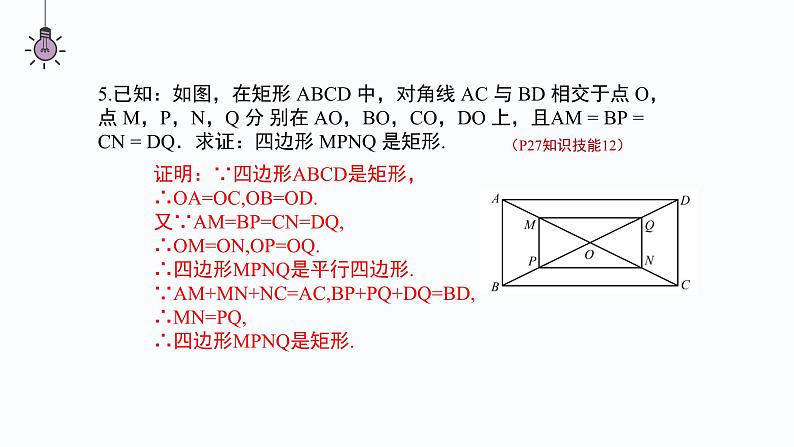
第一章 特殊的平行四边形本章小结平行且相等平行且四边相等平行且四边相等四个角都是直角对角相等邻角互补四个角都是直角互相平分且相等互相垂直平分且相等，每一条对角线平分一组对角互相垂直且平分，每一条对角线平分一组对角一、菱形、矩形、正方形的性质①定义：有一个角是直角的平行四边形.②定理1：对角线相等的平行四边形.③定理2：三个角是直角的四边形.①定义：一组邻边相等的平行四边形.②定理1：四条边都相等的四边形.③定理2：对角线互相垂直的平行四边形.①定义：有一个角是直角且一组邻边相等的平行四边形.②有一组邻边相等的矩形.③有一个角是直角的菱形.二、菱形、矩形、正方形的判定方法考点一：菱形的性质和判定1．一个菱形的两条对角线的长分别为 4 cm 和 8 cm，求它的边长解：如图,菱形ABCD中,对角线AC,BD交于点O,AC=8 cm,BD=4 cm则OA=4 cm,OB=2 cm,∠AOB=90°.根据勾股定理，得AB= = cm.∴该菱形的边长为 cm.（P26知识技能1）2.一个菱形的周长是 200 cm，一条对角线长 60 cm，求：（1）另一条对角线的长度；（2）菱形的面积（P26知识技能4）解：如图,菱形BACD中,对角线AC,BD相交于O，AC=60 cm,周长为200 cm.（1）由题意,得AC⊥BD,AB= ×200=50(cm),OA=OC= AC= 30 cm,OB=OD∴在Rt△AOB中,OB= =40 cm.∴另一条对角线BD=2OB=80 cm.（2）S菱形ABCD= AC∙BD= ×60×80=2400(cm2 ).3.已 知：如 图，A D 是△ABC 的 角 平 分 线，过 点 D 分 别作 AC 和 AB 的平行线，交 AB 于点 E，交 AC 于点 F．求证：四边形 AEDF 是菱形．（P27知识技能8）证明：如图，∵AD平分∠BAC,∴∠1=∠2.∵DE∥AC,∴∠2=∠3.∴∠1=∠3.∴AE=DE.∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.又AE=DE,∴四边形AEDF是菱形.123考点二：矩形的性质和判定（P27知识技能9）4.已知：△ABC 的两条高分别为 BE，CF，点 M 为 BC 的中点． 求证：ME = MF．证明：如图，∵BE⊥AC,ME为Rt△BEC的中线，∴ME= BC.同理得MF= BC.∴ME=MF.5.已知：如图，在矩形 ABCD 中，对角线 AC 与 BD 相交于点 O，点 M，P，N，Q 分 别在 AO，BO，CO，DO 上，且AM = BP = CN = DQ．求证：四边形 MPNQ 是矩形.证明：∵四边形ABCD是矩形，∴OA=OC,OB=OD.又∵AM=BP=CN=DQ,∴OM=ON,OP=OQ.∴四边形MPNQ是平行四边形.∵AM+MN+NC=AC,BP+PQ+DQ=BD,∴MN=PQ,∴四边形MPNQ是矩形.（P27知识技能12）6.如图，在矩形 ABCD 中，AB = 20 cm，BC = 4 cm．动点 P 从点 A 开始沿 AB 边 以 4 cm/s 的速度运动，动点 Q 从点 C 开始沿 CD 边以 1 cm/s 的速度运动．点 P 和 点 Q 分别从点 A 和点 C 同时出发，当其中一点到达终点时，另一点也随之停止运动． 设动点的运动时间为 t s，则当 t 为何值时，四边形 APQD 是矩形？解：依题意AP=4t cm，CQ=t cm，∵四边形ABCD是矩形，∴AB=DC=20 cm，则DQ=DC-CQ=(20-t) cm.当四边形APQD是矩形时，DQ=AP,∴20-t=4t，解得t=4.∴当t=4时，四边形APQD是矩形.（P27知识技能14）考点三：正方形的性质和判定7．如图，若四边形 ABCD 的对角线 AC 与 BD 相交于点 O,且 OA = OB = OC = OD = AB，则四边形 ABCD 是正方形吗？解：由OA=OB= AB,可知OA2+OB2=AB2,则∠AOB=90°.∵OA=OB=OC=OD,∴AC,BD互相垂直平分且相等，∴四边形ABCD是正方形.（P26知识技能2）8.证明：如果四边形两条对角线垂直且相等，那么以它的四边中点为顶点可组成一个正方形.已知：如图，在四边形ABCD中，对角线AC⊥BD,AC=BD,E,F,P,Q分别为边AB,BC,CD,DA的中点.求证：四边形EFPQ为正方形.证明：∵E,Q分别为AB,AD的中点，∴EQ BD同理,得FP BD,EF AC.∴EQ FP.∴四边形EFPQ为平行四边形.∵AC=BD,∴EF=EQ.∴四边形EFPQ为菱形.∵AC⊥BD,∴EF⊥EQ.∴∠QEF=90°.∴四边形EFPQ是正方形.（P26知识技能13）9．如图，四边形 ABCD 是一个正方形，E 是 BC 延长线上一点，且 AC = EC，求 ∠ DAE 的度数．解：∵AC=EC,∴∠E=∠CAE.∵四边形ABCD是正方形,∴AD∥BE.∴∠DAE=∠E=∠CAE.∵∠DAC=∠DAE+∠CAE=45°，∴∠DAE= ∠DAC=22.5°.（P26知识技能6）考点四：综合训练10．（1）如果一个菱形绕对角线的交点旋转90°后，所得 图形与原来的图形重合，那么这个菱形是正方形 吗？为什么？ （2）如果一个四边形绕对角线的交点旋转 90°后，所得图形与原来的图形重合，那么 这个四边形是正方形吗？为什么？解：（1）这个菱形是正方形，理由如下：因为一个菱形绕对角线的交点旋转90°后，所得图形与原来的图形重合，所以这个菱形相邻内角相等.因为菱形的相邻内角互补，所以这个菱形的内角都为90°.所以这个菱形是正方形.（2）这个四边形是正方形，理由如下：因为四边形绕对角线的交点旋转90°后，所得图形与原来的图形重合，所以这个四边形各邻边相等.所以这个四边形为菱形.由（1），这个四边形是正方形.（P26知识技能7）11.已知：如图，在矩形 ABCD 中，对角线 AC 与 BD 相交于点 O，过点 C 作 BD 的平行线，过点 D 作 AC 的平行线，两线相交于点 P．求证：四边形 CODP 是菱形．证明：∵CP∥BD,DP∥AC,∴四边形CODP是平行四边形.∵四边形ABCD是矩形,∴AC=BD.∵OC= AC,OD= BD,∴OC=OD.∴四边形CODP是菱形.（P27知识技能11）12.如图，把一张矩形纸片沿对角线折叠，重合部分是什么图形？试说明理由．解：重合部分△BFD是等腰三角形，理由如下：∵四边形ABCD是矩形，∴AD∥BC,∴∠ADB=∠DBC.由折叠得∠FBD=∠DBC,∴∠FBD=∠ADB.∴BF=DF.∴重合部分△BFD是等腰三角形.（P28数学理解1）课堂小结