北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性精品课件ppt

这是一份北师大版 (2019)必修 第一册1.1 利用函数性质判定方程解的存在性精品课件ppt，共29页。PPT课件主要包含了激趣诱思，知识点拨，数x0，横坐标，答案×，探究一，探究二，探究三，素养形成，当堂检测等内容，欢迎下载使用。

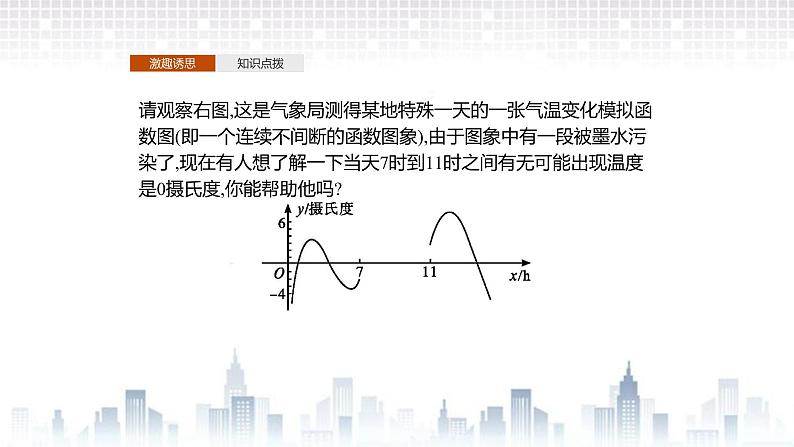
请观察右图,这是气象局测得某地特殊一天的一张气温变化模拟函数图(即一个连续不间断的函数图象),由于图象中有一段被墨水污染了,现在有人想了解一下当天7时到11时之间有无可能出现温度是0摄氏度,你能帮助他吗?
一、函数的零点1.代数定义:使得f(x0)=0的　　　　称为方程f(x)=0的解,也称为函数f(x)的零点. 2.几何定义:f(x)的零点就是函数y=f(x)的图象与x轴交点的　　　　　　. 
名师点析1.函数的零点是一个实数,而不是一个点.例如,函数f(x)=x+1的零点是-1,而不是(-1,0).2.并不是所有的函数都有零点,如f(x)=1,f(x)=x2+1就没有零点.3.若函数有零点,则零点一定在函数的定义域内.4.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的解,也就是函数y1=f(x)与y2=g(x)的图象交点的横坐标.
微练习函数f(x)=x2-1的零点是(　　)A.(±1,0)　　　　B.(1,0)C.0 D.±1
答案:D　解析:解方程f(x)=x2-1=0,得x=±1,因此函数f(x)=x2-1的零点是±1.
二、零点存在定理若函数y=f(x)在闭区间[a,b]上的图象是一条连续的曲线,并且在区间端点的函数值一正一负,即f(a)·f(b)<0,则在开区间(a,b)内,函数y=f(x)至少有一个零点.即在区间(a,b)内相应的方程f(x)=0至少有一个解.
名师点析1.定理要求具备两个条件:(1)函数在区间[a,b]上的图象是一条连续的曲线;(2)f(a)·f(b)<0.这两个条件缺一不可.2.利用函数零点存在定理只能判断出零点是否存在,而不能确定零点的个数.3.若函数y=f(x)的图象在区间[a,b]上是一条连续的曲线,则由f(a)·f(b)<0可以推出函数y=f(x)在区间(a,b)内存在零点,但是由函数y=f(x)在区间(a,b)内存在零点不一定能推出f(a)·f(b)<0.如f(x)=x2在(-1,1)内存在零点,但f(-1)·f(1)>0.4.如果单调函数y=f(x)在区间[a,b]上的图象是一条连续的曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有唯一的零点,即存在唯一的x0∈(a,b),使得f(x0)=0,这个x0也就是方程f(x)=0的解.
微练习1函数y=f(x)的图象是在闭区间[a,b]上的一条连续不断的曲线.若f(a)·f(b)>0,则f(x)在区间(a,b)内没有零点.(　　)微练习2函数f(x)=x3+2x+1的零点一定位于下列哪个区间上(　　)A.[-2,-1]　　　　B.[-1,0]C.[0,1] D.[1,2]
答案:B　解析:因为f(-2)=-11<0,f(-1)=-2<0,f(0)=1>0,f(1)=4>0,f(2)=13>0,所以f(-1)·f(0)<0.所以f(x)的零点在区间[-1,0]上.
求函数的零点例1判断下列函数是否存在零点,如果存在,请求出零点.(1)f(x)=-8x2+7x+1;(2)f(x)=1+lg3x;(3)f(x)=4x-16.分析可通过解方程f(x)=0求得函数的零点.
反思感悟因为函数f(x)的零点就是方程f(x)=0的解,也是函数y=f(x)的图象与x轴交点的横坐标,所以求函数的零点通常有两种方法:一是代数法,令f(x)=0,通过求方程f(x)=0的解求得函数的零点;二是几何法,画出函数y=f(x)的图象,图象与x轴交点的横坐标即函数的零点.
变式训练1已知函数f(x)=x2+3(m+1)x+n的零点是1和2,求函数y=lgn(mx+1)的零点.
解:由题意知函数f(x)=x2+3(m+1)x+n的零点为1和2,则1和2是方程x2+3(m+1)x+n=0的解.
所以函数y=lgn(mx+1)的解析式为y=lg2(-2x+1).令lg2(-2x+1)=0,得x=0.所以函数y=lg2(-2x+1)的零点为0.
函数零点个数的判断例2判断下列函数零点的个数:(1)f(x)=(x2-4)lg2x;
(3)f(x)=2x+lg(x+1)-2.
解:(1)令f(x)=0,得(x2-4)lg2x=0,因此x2-4=0或lg2x=0,解得x=±2或x=1.又因为函数定义域为(0,+∞),所以x=-2不是函数的零点,故函数有2和1两个零点.
画出函数g(x)和h(x)的图象如图所示.由图象可知,两个函数图象只有一个交点,故函数只有一个零点.
(3)(方法一)∵f(0)=1+0-2=-1<0,f(2)=4+lg 3-2=2+lg 3>0,∴f(x)=0在(0,2)上必定存在实根.又f(x)=2x+lg(x+1)-2在区间(-1,+∞)上为增函数,故f(x)有且只有一个零点.(方法二)令h(x)=2-2x,g(x)=lg(x+1),在同一平面直角坐标系中作出h(x)与g(x)的图象,如图所示.由图象知g(x)=lg(x+1)和h(x)=2-2x的图象有且只有一个公共点,即f(x)=2x+lg(x+1)-2有且只有一个零点.
反思感悟判断函数零点个数的常用方法1.解方程f(x)=0,方程f(x)=0解的个数就是函数f(x)零点的个数.2.直接作出函数f(x)的图象,图象与x轴交点的个数就是函数f(x)零点的个数.3.f(x)=g(x)-h(x)=0,得g(x)=h(x),在同一平面直角坐标系中作出y1=g(x)和y2=h(x)的图象,则两个图象交点的个数就是函数y=f(x)零点的个数.4.若证明一个函数的零点唯一,也可先由零点存在定理判断出函数有零点,再证明该函数在定义域内单调.
变式训练2(1)若abc≠0,且b2=ac,则函数f(x)=ax2+bx+c的零点的个数是(　　)A.0B.1C.2D.1或2
答案:A　解析:∵b2=ac,∴方程ax2+bx+c=0的判别式Δ=b2-4ac=b2-4b2=-3b2.∵abc≠0,∴b≠0.因此Δ<0.故函数f(x)=ax2+bx+c的零点个数为0.
(2)判断函数f(x)=x-3+ln x的零点个数.
解:(方法一)令f(x)=x-3+ln x=0,则ln x=3-x.在同一平面直角坐标系中分别画出函数y=ln x与y=-x+3的图象,如图所示.由图可知函数y=ln x与y=-x+3的图象只有一个公共点,即函数f(x)=x-3+ln x只有一个零点.(方法二)因为f(3)=ln 3>0,
所以f(3)·f(2)<0,说明函数f(x)=x-3+ln x在区间(2,3)内有零点.又f(x)=x-3+ln x在区间(0,+∞)上是增函数,所以原函数只有一个零点.
已知零点个数求参数的取值范围
A.(1,2]B.[1,+∞)C.[1,2)D.[1,2]
例4已知a是实数,函数f(x)=2|x-1|+x-a,若函数y=f(x)有且仅有两个零点,则实数a的取值范围是　　　　　. 分析把函数f(x)的两个零点问题转化为函数y=2|x-1|+x与y=a的图象有且仅有两个交点的问题,画出两个函数的图象,然后利用数形结合思想求出参数a的范围.
答案: (1,+∞)　 解析:函数f(x)=2|x-1|+x-a有且仅有两个零点,即函数y=2|x-1|+x与y=a的图象有且仅有两个交点.分别作出函数y=2|x-1|+x与y=a的图象,如图所示.由图易知,当a>1时,两函数的图象有且仅有两个不同的交点,故实数a的取值范围是(1,+∞).
反思感悟已知函数有零点(方程有根)求参数的方法1.直接法:根据题设条件构建关于参数的不等式(组),通过解不等式(组)确定参数的取值范围.2.数列结合法:先对f(x)的解析式变形,将f(x)=0转化为h(x)=g(x)(h(x),g(x)的图象易画出),在同一平面直角坐标系中画出函数h(x),g(x)的图象,然后利用数形结合思想求解.
变式训练3(2020福建厦门双十中学高一检测)已知函数f(x)=3ax-1-2a在区间(-1,1)上存在零点,则(　　)
答案:C　解析:∵f(x)=3ax-1-2a在(-1,1)上单调,且存在零点,∴f(-1)·f(1)<0,即(-3a-1-2a)·(3a-1-2a)=(-5a-1)·(a-1)<0,∴a>1
二次函数的零点综合问题典例 已知二次函数f(x)=x2-(k-2)x+k2+3k+5.(1)当函数f(x)有两个不同零点时,求k的取值范围;(2)若-1和-3是函数的两个零点,求k的值;(3)若函数的两个不同零点是α,β,求α2+β2关于k的关系式h(k).分析本题考查对二次函数零点的理解及零点的性质.本题中的函数f(x)是二次函数,因此其零点的判断和零点的性质问题可以转化为二次方程解的判断或解的性质.
规范解答(1)令f(x)=0,得x2-(k-2)x+k2+3k+5=0.由Δ=(k-2)2-4(k2+3k+5)=-3k2-16k-16>0,知3k2+16k+16<0,即(3k+4)(k+4)<0,
(2)∵-1和-3是函数f(x)的两个零点,∴-1和-3是方程x2-(k-2)x+k2+3k+5=0的两个解.
(3)∵α,β是函数f(x)的两个不同零点,∴α,β是方程x2-(k-2)x+k2+3k+5=0的两个实数根,∴α+β=k-2,αβ=k2+3k+5.∴α2+β2=(α+β)2-2αβ=(k-2)2-2(k2+3k+5)=-k2-10k-6.
规律总结1.若二次方程ax2+bx+c=0(a≠0)的两个解是x1,x2,
2.本题中如果忽视Δ,将会影响α2+β2的范围而导致出错.
1.如下图四个函数图象,在区间(-∞,0)内存在零点的函数是(　　)
答案:B　解析:只有选项B中的函数图象与x轴的负半轴有交点.
2.函数f(x)=lg5(x-1)的零点是(　　)A.0B.1C.2D.33.若x0是方程ln x+x=4的解,则x0所在的区间是(　　)A.(0,1) B.(1,2)C.(2,3)D.(3,4)
答案:C　解析:令lg5(x-1)=0,解得x=2,所以函数f(x)=lg5(x-1)的零点是2,故选C.
答案:C　解析:设f(x)=ln x+x-4,则f(1)=-3<0,f(2)=ln 2-2<0,f(3)=ln 3-1>0,f(4)=ln 4>0,则x0∈(2,3).
4.已知函数y=ax2-x-1只有一个零点,则实数a的值为　　　　　. 
解析:当a=0时,函数为y=-x-1,显然该函数的图象与x轴只有一个公共点,即函数只有一个零点.当a≠0时,函数y=ax2-x-1为二次函数.∵函数y=ax2-x-1只有一个零点,∴方程ax2-x-1=0有两个相等的实数解.