



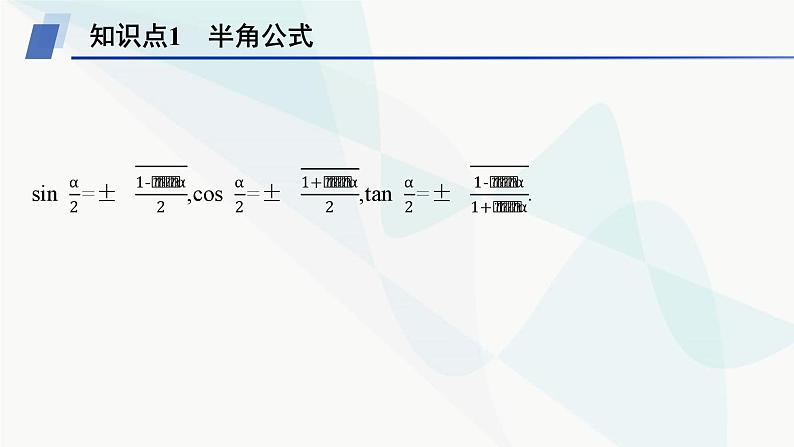


所属成套资源:全套人教A版高中数学必修第一册课时教学课件
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换示范课课件ppt
展开
这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换示范课课件ppt,共42页。PPT课件主要包含了知识点1半角公式等内容,欢迎下载使用。
1.能运用和差角的正弦、余弦公式及二倍角公式等进行简单的恒等变换(包括推导出积化和差、和差化积、半角公式,这三组公式不要求记忆).2.能利用三角恒等变换对三角函数式化简、求值和证明.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
目 录 索 引
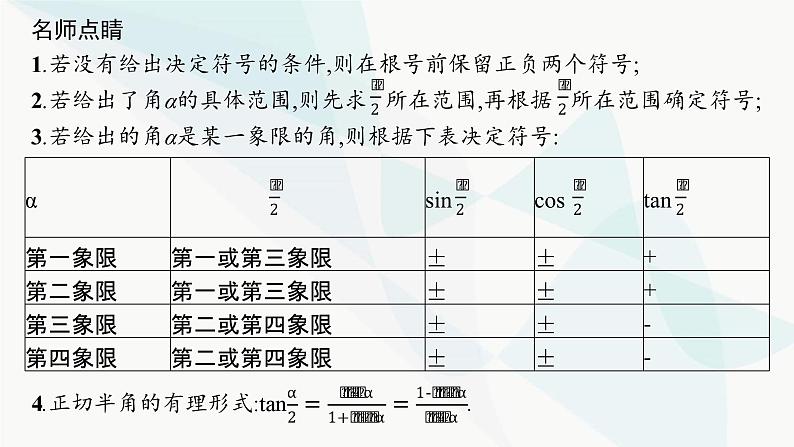
名师点睛1.若没有给出决定符号的条件,则在根号前保留正负两个符号;2.若给出了角α的具体范围,则先求 所在范围,再根据 所在范围确定符号;3.若给出的角α是某一象限的角,则根据下表决定符号:
过关自诊1.判断正误.(正确的画√,错误的画×)
知识点2 辅助角公式
2.[北师大版教材习题]求函数f(x)=|sin x+cs x|的最小正周期.
知识点3 积化和差、和差化积公式(补充)
探究点一 半角公式的应用
角度1.用半角公式解决求值问题
角度2.用半角公式解决证明问题
规律方法 证明问题中的“三变”(1)变角:三角变换时通常先寻找式子中各角之间的联系,通过拆、凑等手段消除角之间的差异,合理选择联系它们的公式.(2)变名:观察三角函数种类的差异,尽量统一函数的名称,如统一为弦或统一为切.(3)变式:观察式子的结构形式的差异,选择适当的变形途径.如升幂、降幂、配方、开方等.
探究点二 积化和差、和差化积公式的应用
变式探究 在例3(1)中,若不利用积化和差公式,如何求解?
规律方法 1.当条件或结论式比较复杂时,往往先将它们化为最简形式,再求解.2.当要证明的不等式一边复杂,另一边非常简单时,往往从复杂的一边入手证明,类似于化简.
变式训练2 已知sin A+sin 3A+sin 5A=a,cs A+cs 3A+cs 5A=b.求证:(2cs 2A+1)2=a2+b2.
证明 由题意知(sin A+sin 5A)+sin 3A=2sin 3Acs 2A+sin 3A=a,(cs A+cs 5A)+cs 3A=2cs 3Acs 2A+cs 3A=b,∴sin 3A(2cs 2A+1)=a,①cs 3A(2cs 2A+1)=b.②两式平方相加,得(2cs 2A+1)2=a2+b2.
探究点三 辅助角公式的应用
【例4】 将下列各式化为y=Asin(ωx+φ)+k的形式:
(2)y=cs 2x(sin 2x+cs 2x);
本节要点归纳1.知识清单:(1)半角公式,辅助角公式.(2)三角恒等变换的综合应用.2.方法归纳:转化与化归.3.常见误区:半角公式符号的判断.
5.已知2cs2x+sin 2x=Asin(ωx+φ)+b(A>0,b∈R),则A= ,b= .
(1)将f(x)化为Asin(ωx+φ)(A>0,ω>0)的形式;(2)求f(x)的最小正周期;(3)求f(x)的最大值和最小值.
相关课件
这是一份必修 第一册5.5 三角恒等变换作业课件ppt,共16页。
这是一份人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换图片ppt课件,共27页。PPT课件主要包含了目录索引等内容,欢迎下载使用。
这是一份人教A版 (2019)必修 第一册5.5 三角恒等变换作业ppt课件,共16页。PPT课件主要包含了BCD等内容,欢迎下载使用。











