湘教版九年级上册第3章 图形的相似3.4 相似三角形的判定与性质优质教学设计

回顾知识

+

导入新课

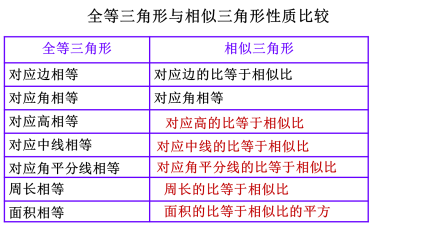
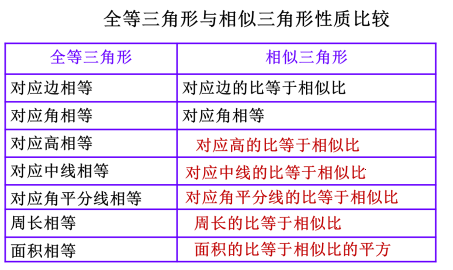
在前面的学习中，我们已经学习有关两个三角形相似的部分性质。今天，我们将继续探究其他的性质，在上新课之前，我们一起回顾下之前学过的知识：

全等三角形与相似三角形的性质

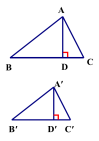
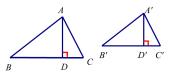
【导入新课】接下来，我们一起来看个问题：

问题1 ：若△A’B’C’∽△ABC，相似比为k，那么它们的周长比是多少？

解：∵

∴A’B’=kab，B’C’=kBC，C’A’=kCA.

∴

结论：相似三角形周长的比等于相似比.

    问题2 ：若△A’B’C’∽△ABC，相似比为k，那么它们的面积比是多少？

解：分别作BC，B’C’上的高AD，A’D’ ．

     ∵

∴=k·k=k²

结论：相似三角形面积的比等于相似比的平方.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

从刚刚导入新课的探究中，我们可以得到两个三角形相似的其他性质：

1. 相似三角形周长的比等于相似比，

2.相似三角形面积的比等于相似比的平方.

符号表示：

∵ ΔABC ∽ ΔA’B’C’， ΔABC与ΔA’B’C’的相似比为k

∴=k，k².

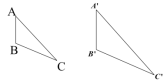
接下来，我们看一些具体的例子：

    【例1】已知：△ABC∽△A’B’C’ ，它们的周长分别为60cm和72cm，且AB=15cm，B’C’=24cm.求：BC，AC，A′B′，A′C′.

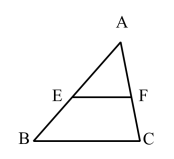
解：∵ △ABC∽△A’B’C’，它们周长分别为60cm和72cm，

∴它们的相似比为60：72=5：6.

又∵AB=15cm，B’C’=24cm

∴A′B′=18，BC=20.

∴A′C′=72-24-18=30，

   AC=60-15-20=25.

【例2】△ABC中，EF//BC，,S四边形BCEF=8.求S△ABC.            

解：∵ △ABC中，EF//BC

∴ △ABC∽ △ACD

又∴

∴=

∵ S四边形BCEF=8

∴ S△AEF=1，∴ S△ABC=9.

【例3】已知△ABC与△A’B’C’ 的相似比为， 且S△ABC+ S△A’B’C’=91，求△A’B’C’的面积.

解：∵△ABC与△A’B’C’ 的相似比为，

∴ =，即= 

又S△ABC+ S△A’B’C’=91

∴ + S△A’B’C’=91

∴=63.

现在我们一起结合全等三角形回顾下本节课的知识：

结合导入的思考和老师的讲解，利用探究理解和掌握成两个三角形相似的性质.

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握两个三角形相似的性质。

让学生知道本节课的学习内容，同时加深对知识的理解和巩固，同时让学生知道本节课的重点。

课堂练习

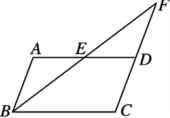
1．两个相似三角形的面积比为9∶4，则对应边的中线之比为　3:2     　.

2．两个相似三角形的周长之比为2∶3，则它们的面积比为　 4:9   　.

3．△ABC∽△DEF，且AB∶DE＝3∶4，则△ABC与△DEF的周长之比为　3:4  　.

4．如果两个相似多边形面积的比为1∶5，那么它们的相似比为(  D )

A．1∶25           B．1∶5 

C．1∶2.5     D．1∶

  5.如图，在▱ABCD中，点E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F，则△EDF与△BCF的周长之比是(　              　)

A．1∶2              B．1∶3　

C．1∶4              D．1∶5

∵四边形ABCD是平行四边形，

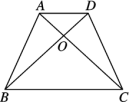
∴AD＝BC且AD∥BC，

又点E是AD边上的中点，∴AD＝2DE，

∴BC＝2DE，

∵AD∥BC，∴△EDF∽△BCF，∴=

  6．如图，梯形ABCD中，AD∥BC且AD∶BC＝1∶3，对角线AC、BD交于点O，求S△AOD∶S△BOC∶S△AOB.

解：∵AD∥BC，易得△AOD∽△COB，

∴S△AOD∶S△COB＝(1∶3)＝1∶9，

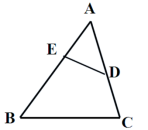
又OD∶OB＝AD∶BC＝1∶3，

∴SAOD∶S△AOB＝OD∶OB＝1∶3，

∴S△AOD∶S△BOC∶S△AOB＝1∶9∶3.

7．如图所示，D、E分别是AC、AB上的点，已知△ABC的面积为100cm2  ，且  求四边形BCDE的面积.　　　　

解：∵∠BAD=∠DAE，且，

∴△ABC∽△ADE

∴它们的相似比为5：3，面积比为25：9.

又∵△ABC的面积为100 cm  ，

∴△ADE的面积为36 cm.

∴四边形BCDE的面积为100-36=64（cm） .

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

相似三角形的性质

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

相似三角形的性质

借助板书，让学生知识本节课的重点。

作业

教材第87页练习第1、2题.