北师大版 (2019)必修 第二册6.1 探究w对y=sinwx的图象的影响导学案

这是一份北师大版 (2019)必修 第二册6.1 探究w对y=sinwx的图象的影响导学案，共11页。

1.6.1 探究ω对y＝sin ωx的图象的影响
1.6.2 探究φ对y＝sin(x＋φ)的图象的影响

1.函数y＝sin(ωx＋φ)的性质
(1)定义域：R.
(2)值域：[－1,1]．
(3)周期：最小正周期T＝eq \f(2π,|ω|).
(4)当ωx＋φ＝2kπ＋eq \f(π,2)，k∈Z时，y最大值为1；
当ωx＋φ＝2kπ－eq \f(π,2)，k∈Z时，y最小值为－1.
其他性质：函数y＝sin(ωx＋φ)周期的倒数eq \f(1,T)＝eq \f(ω,2π)为函数y＝sin(ωx＋φ)的频率．函数y＝sin(ωx＋φ)中通常称φ为初相，ωx＋φ为相位．
2.常数ω，φ对函数y＝sin(ωx＋φ)图象的影响
(1)ω(ω>0)对函数图象的影响
y＝sin xeq \(――――――――――――――→,\s\up17(图象上点的纵坐标保持不变),\s\d15(横坐标变为原来的\f(1,ω)))y＝sin ωx.
(2)φ对函数图象的影响
y＝sin xeq \(――――――――――――――――――→,\s\up17(当φ>0时，图象向左平移|φ|个单位),\s\d15(当φ<0时，图象向右平移|φ|个单位))y＝sin(x＋φ)．
研习1 五点作图法
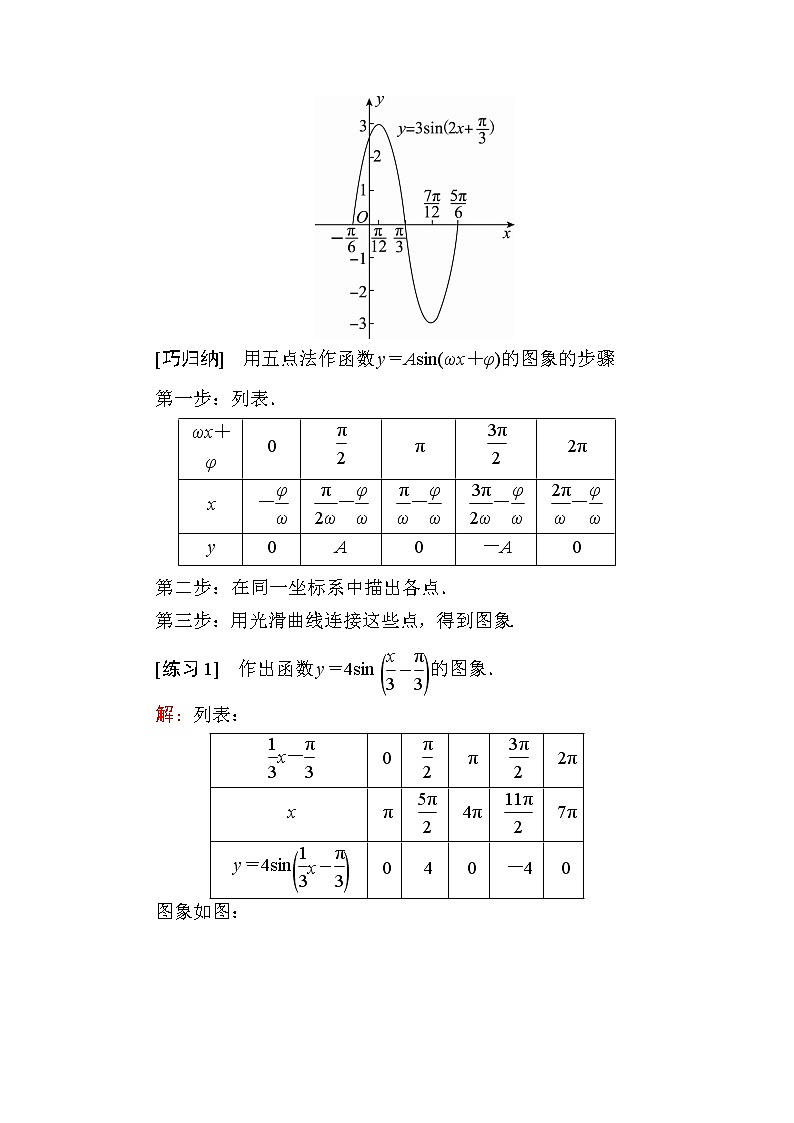
[典例1] 作出函数y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象．
[自主记]
[分析] 根据函数的解析式，用五点法作函数的图象．
[解] 列表：
描点、连线得到函数在一个周期内的简图，利用函数的周期性，可以把上述简图向左、右扩展，就得到y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，x∈R的简图．
[巧归纳] 用五点法作函数y＝Asin(ωx＋φ)的图象的步骤
第一步：列表．
第二步：在同一坐标系中描出各点．
第三步：用光滑曲线连接这些点，得到图象.
[练习1] 作出函数y＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,3)－\f(π,3)))的图象．
解：列表：
图象如图：
研习2 函数图象的平移变换
[典例2] 为了得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))的图象，可以将函数y＝cs 2x的图象( )
A．向右平移eq \f(π,6)个单位长度 B．向左平移eq \f(π,6)个单位长度
C．向右平移eq \f(π,3)个单位长度 D．向左平移eq \f(π,3)个单位长度
[自主记]
[答案] C
[解析] 由于y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))＝cseq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－\b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3)－2x))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(2π,3)))＝cseq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))))，为得到该函数的图象，只需将y＝cs 2x的图象向右平移eq \f(π,3)个单位长度.
[巧归纳] 三角函数的平移变换问题的分类及策略
(1)已知两个函数的解析式判断其图象间的平移关系时，首先将解析式化简为y＝Asin(ωx＋φ)的形式，即确定A，ω，φ的值，然后确定平移的方向和单位．
(2)确定函数y＝sin x的图象经过变换后图象对应的函数解析式，关键是明确左右平移的方向和横纵坐标伸缩的量，确定出A，ω，φ的值.
[练习2] 要得到函数y＝sineq \f(1,2)x的图象，只需将函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x＋\f(π,4)))的图象( )
A．向左平移eq \f(π,4)个单位长度
B．向右平移eq \f(π,4)个单位长度
C．向左平移eq \f(π,2)个单位长度
D．向右平移eq \f(π,2)个单位长度
答案：D
研习3 函数图象的伸缩变换
[典例3] (1)将函数y＝sin x的图象上各点的横坐标扩大为原来的2倍，纵坐标不变，则所得图象对应的函数为( )
A．y＝2sin x B．y＝eq \f(1,2)sin x
C．y＝sin 2x D．y＝sineq \f(1,2)x
(2)如何由y＝sin x的图象得到函数y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象？
[自主记]
[答案] (1)D
[解析] 由题意知，最小正周期变为原来的2倍，即4π，所以eq \f(2π,ω)＝4π，因此ω＝eq \f(1,2).所以所得图象对应的函数解析式为y＝sin eq \f(1,2)x.
(2)[解] 解法一：y＝sin x的图象
解法二：y＝sin x的图象
[巧归纳] 三角函数图象伸缩变换的两种思路
[练习3] 把函数y＝sin(ωx＋φ)(ω>0，|φ|<π)的图象向左平移eq \f(π,6)个单位长度，再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得图象的函数解析式为y＝sin x，则( )
A．ω＝2，φ＝eq \f(π,6) B．ω＝2，φ＝－eq \f(π,3)
C．ω＝eq \f(1,2)，φ＝eq \f(π,6) D．ω＝eq \f(1,2)，φ＝eq \f(π,12)
答案：B

1.把函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,4)))的图象向左平移eq \f(π,8)个单位长度，所得到的图象对应的函数是( )
A．奇函数
B．偶函数
C．既是奇函数也是偶函数
D．非奇非偶函数
答案：A
解析：y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,4)))＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8)))))，向左平移eq \f(π,8)个单位长度后为y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,8)＋\f(π,8)))))＝sin 2x，为奇函数，故选A．
2.为了得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象，只需把函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的图象( )
A．向左平移eq \f(π,4)个单位长度
B．向右平移eq \f(π,4)个单位长度
C．向左平移eq \f(π,2)个单位长度
D．向右平移eq \f(π,2)个单位长度
答案：B
解析：由y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))eq \(――→,\s\up17(x→x＋φ))y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2x＋φ＋\f(π,6)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))，即2x＋2φ＋eq \f(π,6)＝2x－eq \f(π,3)，解得φ＝－eq \f(π,4)，即向右平移eq \f(π,4)个单位长度.
3.用“五点法”画函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,3)))(ω>0)在一个周期内的简图时，五个关键点是eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,6)，0))，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)，2))，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)，0))，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7,12)π，－2))，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,6)，0))，则ω＝________.
答案：2
解析：周期T＝eq \f(5π,6)－eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,6)))＝π.∴eq \f(2π,ω)＝π，ω＝2.
4.若将函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(5π,6)))(ω>0)的图象向右平移eq \f(π,3)个单位长度后，与函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,4)))的图象重合，则ω的最小值为________．
答案：eq \f(7,4)
解析：y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(5π,6)))的图象向右平移eq \f(π,3)个单位后得到y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(w\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,3)))＋\f(5,6)π))，
即y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(5,6)π－\f(ωπ,3)))，
故eq \f(5π,6)－eq \f(ωπ,3)＋2kπ＝eq \f(π,4)(k∈Z)，
即eq \f(ωπ,3)＝eq \f(7π,12)＋2kπ，ω＝eq \f(7,4)＋6k(k∈Z)．
∵ω>0，∴ω的最小值为eq \f(7,4).
5.已知函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))＋1.
(1)用“五点法”画出函数的草图；
(2)函数图象可由y＝sin x的图象怎样变换得到？
解：(1)列表：
描点、连线，如图所示．
将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))＋1在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,8)，\f(7π,8)))上的图象向左(右)平移kπ(k∈Z)个单位，即可得到y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4)))＋1的整个图象．
[误区警示] 在函数图象的变换过程中，易将平移方向或平移长度弄错 由y＝sin x的图象变换为y＝sin(ωx＋φ)(ω>0)的图象时，若先由y＝sin x的图象变换为y＝sin ωx的图象，再由y＝sin ωx的图象变换为y＝sin(ωx＋φ)的图象，则左右平移eq \f(|φ|,ω)个单位长度，很多人都直接左右平移|φ|个单位长度，从而导致错误．
[示例] 将函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象先沿x轴向右平移eq \f(π,4)个单位长度，再把所得图象上各点的横坐标缩短到原来的eq \f(1,2)，求与最终的图象对应的函数的解析式．
[错解1] 将原函数的图象沿x轴向右平移eq \f(π,4)个单位长度后，与其对应的函数的解析式为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)－\f(π,4)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(7π,12)))，再将所得图象上所有点的横坐标缩短到原来的eq \f(1,2)，则与其对应的函数的解析式为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x－\f(7π,12))).
[错解2] 将原函数的图象沿x轴向右平移eq \f(π,4)个单位长度后，与其对应的函数的解析式为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)－\f(π,4)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(7π,12)))，再将所得图象上所有点的横坐标缩短到原来的eq \f(1,2)，则与其对应的函数的解析式为y＝sin 2eq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(7π,12)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x－\f(7π,6)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(5π,6))).
[错因分析] 以上两种解法都是错误的，错解产生的根本原因是没有抓住变换的对象．[错解1]在进行平移变换时，错误地把2x看成了变换对象，[错解2]在平移变换和伸缩变换上都犯了错误.
[正解] 将原函数的图象沿x轴向右平移eq \f(π,4)个单位长度后，与其对应的函数的解析式为y＝sin 2eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)－\f(π,4)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(5π,6)))，再将所得图象上所有点的横坐标缩短到原来的eq \f(1,2)，则与其对应的函数的解析式为y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x－\f(5π,6))).
新课程标准
学业水平要求
1.结合具体实例，了解y＝sin(ωx＋φ)的实际意义；
2．能借助图象了解参数ω，φ的意义；
3．了解参数ω，φ对函数图象的影响.
1.结合教材实例理解参数ω，φ的意义．(数学抽象)
2．结合教材实例掌握参数ω，φ对正弦函数图象的影响．(直观想象)
3．会利用参数ω，φ对函数图象的影响解决相关的问题．(直观想象、逻辑推理)
课前篇·自主学习预案
课堂篇·研习讨论导案
2x＋eq \f(π,3)
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－eq \f(π,6)
eq \f(π,12)
eq \f(π,3)
eq \f(7π,12)
eq \f(5π,6)
y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))
0
3
0
－3
0
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－eq \f(φ,ω)
eq \f(π,2ω)－eq \f(φ,ω)
eq \f(π,ω)－eq \f(φ,ω)
eq \f(3π,2ω)－eq \f(φ,ω)
eq \f(2π,ω)－eq \f(φ,ω)
y
0
A
0
－A
0
eq \f(1,3)x－eq \f(π,3)
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
π
eq \f(5π,2)
4π
eq \f(11π,2)
7π
y＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)x－\f(π,3)))
0
4
0
－4
0
达标篇·课堂速测演习
2x＋eq \f(π,4)
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－eq \f(π,8)
eq \f(π,8)
eq \f(3π,8)
eq \f(5π,8)
eq \f(7π,8)
y
1
2
1
0
1