高中数学4.3.2 独立性检验课后复习题

这是一份高中数学4.3.2 独立性检验课后复习题，共12页。试卷主要包含了函数的大致图象是，曲线在点处的切线方程为，设球的半径为时间t的函数等内容，欢迎下载使用。
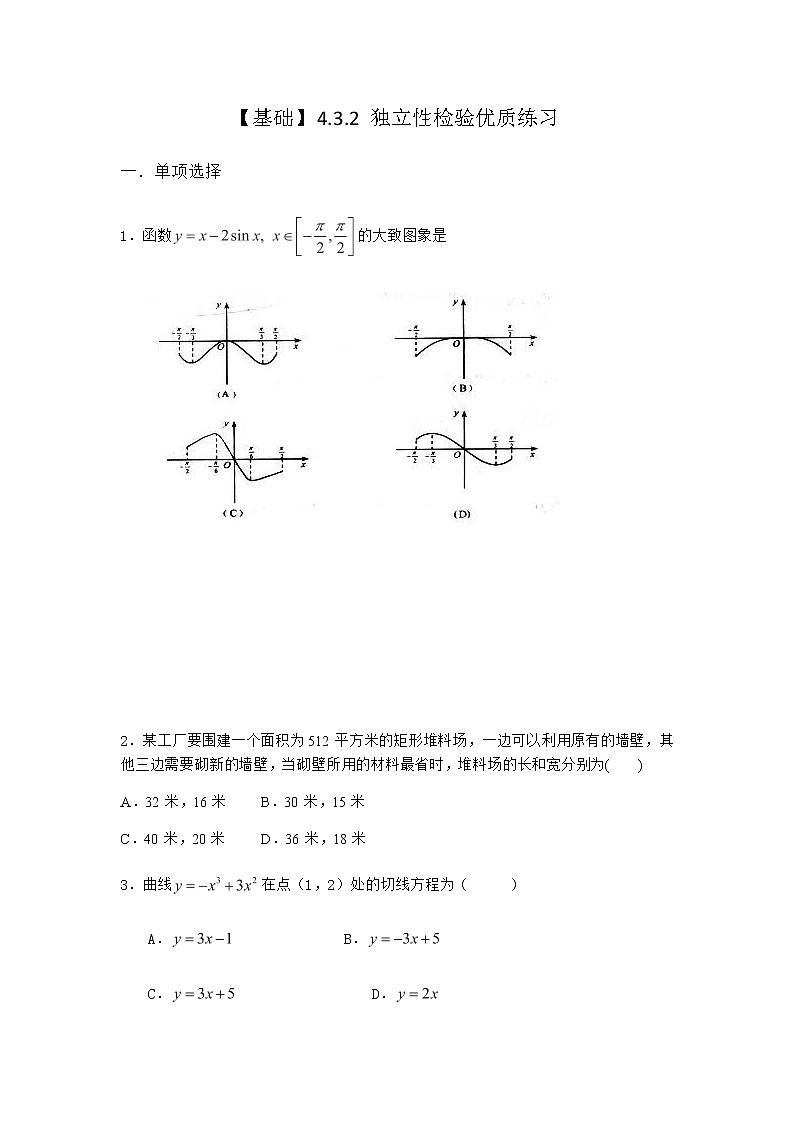
【基础】4.3.2 独立性检验优质练习一．单项选择1．函数的大致图象是           2．某工厂要围建一个面积为512平方米的矩形堆料场，一边可以利用原有的墙壁，其他三边需要砌新的墙壁，当砌壁所用的材料最省时，堆料场的长和宽分别为(　　)A．32米，16米   B．30米，15米C．40米，20米   D．36米，18米3．曲线在点（1，2）处的切线方程为 (      ) A．               B． C．                  D．4．在日常生活中，石子是我们经常见到的材料. 现有一棱长均为3的正四棱锥石料的顶角和底面一个角损坏，某雕刻师计划用一平行于底面的截面截四棱锥分别交，，，于点，，，，做出一个体积最大的新的四棱锥，为底面的中心，则新四棱锥的表面积为（    ）A． B． C． D．5．设底为正三角形的直棱柱的体积为V，那么其表面积最小时，底面边长为(　　)．A.    B.   C.    D．26．设球的半径为时间t的函数．若球的体积以均匀速度C增长，则球的表面积的增长速度与球半径（ ）A．成正比，比例系数为C B．成正比，比例系数为2CC．成反比，比例系数为C D．成反比，比例系数为2C7．设函数在区间上的导函数为， 在区间上的导函数为，若在区间上恒成立，则称函数在区间上为“凸函数”．已知，若对任意的实数满足时，函数在区间上为“凸函数”，则的最大值为（   ）A.     B.     C.     D. 8．一物体在曲线s=+2t2上运动，则该物体在t=3s时的瞬时速度(位移单位：m，时间单位：s)为　(　　)A.m/s                       B. m/sC.m/s                      D.m/s9．已知函数f(x)在R上可导，且f(x)=x2+2xf ′(2），则与的大小关系为（   ）A. f（-1）= f（1）                B. f（-1）＞f（1）C. f（-1）＜ f（1）               D.不确定10．函数的图象在点处的切线与两坐标轴围成的三角形面积为（   ）A.     B.     C.     D. 11．若一球的半径为r，则内接于球的圆柱的侧面积最大为(　　)A．2πr2    B．πr2      C．4πr2    D. πr212．若一个四棱锥底面为正方形, 顶点在底面的射影为正方形的中心, 且该四棱锥的体积为,当其外接球的体积最小时, 它的高为（   ）A．                 B．                C．               D．13．将长为的铁丝截成12段，搭成一个正四棱柱的骨架，以此骨架做成一个正四棱柱容器，则此容器的最大容积为（    ）A． B． C． D．14．某品牌小汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/时）的函数解析式为.若要使该汽车行驶200千米时的油耗最低，则汽车匀速行驶的速度应为（   ）A. 60千米/时    B. 80千米/时    C. 90千米/时    D. 100千米/时15．一矩形的一边在轴上，另两个顶点在函数的图像上，如图，则此矩形绕轴旋转而成的几何体的体积的最大值是（   ）A．        B．        C．        D．
参考答案与试题解析1．【答案】【解析】2．【答案】A【解析】要求材料最省就是要求新砌的墙壁总长度最短，如图所示，设场地宽为x米，则长为米，因此新墙总长度L＝2x＋ (x>0)，则L′＝2－.令L′＝0，得x＝±16.∵x>0，∴x＝16. 当x＝16时，L极小值＝Lmin＝64，∴堆料场的长为＝32(米)．3．【答案】A【解析】由导数的几何意义知：切线的斜率为3，所以切线方程为，选A.4．【答案】A【解析】根据题意，结合棱锥的性质可知其为相似几何体，得到其边的比值，利用锥体体积公式，列出式子，应用导数求得最值，之后应用表面积公式求得结果.详解：因为平面与平面平行，所以四边形与四边形相似，所以四边形为正方形，设，所以，易知四棱锥与四棱锥的高的比为，设，，则当时，，当时，，所以时，取得最大值.此时，所以四棱锥的表面积为.故选：A.【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有相似几何体，锥体的体积公式，锥体的表面积公式，应用导数解决其最值，属于中档题目.5．【答案】C【解析】设底面边长为x，侧棱长为l，则V＝x2·sin 60°·l，∴l＝，∴S表＝2S底＋3S侧＝x2·sin 60°＋3·x·l＝x2＋，S′表＝x－.令S′表＝0，∴x3＝4V，即x＝.又当x∈时，S′表<0；当x∈，S′表>0，∴当x＝时，表面积最小．6．【答案】D【解析】详解：由题意可知球的体积为,则，由此可得,而球的表面积为，所以.故选：D.【点晴】本题考查球的表面积，考查逻辑思维能力，计算能力.求出球的表达式，然后求球的导数，推出，利用面积的导数是体积，求出球的表面积的增长速度与球的半径的比例关系.本题是将几何体的表面积和导数的知识结合到一起，对学生的能力考查比较着重，综合性较强.7．【答案】C【解析】由于，所以，因为在区间上为“凸函数”，所以 在区间上恒成立， 对时恒成立，即对恒成立，所以，解得，其对应的可行域如下图所示，则的最大值是，故选C.考点：1．导数在函数研究中的应用；2．线性规划.【方法点晴】本题是一个关于导数在函数研究中的应用以及线性规划方面的综合性问题，属于中档题.解决本题的基本思路及切入点是：根据题目条件首先对函数进行两次求导，列出关于的不等式组，并且将上述不等式组转换成关于未知数 上的不等式，进而得到关于的不等式，再结合线性规划即可求得的最大值.8．【答案】D【解析】∵s=-+2t2，∴s′=-++4t，∴当t=3s时的瞬时速度为m/s.9．【答案】【解析】10．【答案】C【解析】分析：根据导函数在函数上点的斜率为导函数的性质，可求得切线方程为，求出切线方程与x轴．y轴的交点即可求出三角形面积。详解：因为 ，所以函数在处的切线斜率为当时， ，所以点的坐标为所以切线方程为切线与 轴交点为 ，与 轴交点为所以围成的三角形面积为所以选C点睛：本题考查了导函数的简单应用，导函数的意义为在某一点切线方程的斜率，关键是区分点是否在曲线上，属于简单题。11．【答案】A【解析】如图，设内接圆柱的底面半径为R，母线长为l，则R＝rcos θ，l＝2rsinθ. ∴S侧＝2πR·l＝2πrcosθ×2rsinθ＝4πr2sinθcosθ.∴由S′＝4πr2(cos2θ－sin2θ)＝0，得θ＝.∴当θ＝，即R＝r时，S侧最大，且S侧最大值为2πr2. 12．【答案】A【解析】设四棱锥底面正方形边长为，四棱锥高为，外接球半径为，则，所以，因为，所以时取唯一一个极小值，也是最小值，即外接球的体积最小，因此选A.考点：导数实际应用【方法点睛】利用导数解答函数最值的一般步骤：第一步：利用f′（x）＞0或f′（x）＜0求单调区间；第二步：解f′（x）＝0得两个根x1．x2；第三步：比较两根同区间端点的大小；第四步：求极值；第五步：比较极值同端点值的大小．13．【答案】C【解析】设正四棱柱的底面边长为xcm，则正四棱柱的高是（72﹣8x）＝18﹣2x，表示出体积，求导数，即可求出此四棱柱的高，从而得到体积.【详解】解：设正四棱柱的底面边长为xcm，则正四棱柱的高是（72﹣8x）＝18﹣2x，所以体积V＝Sh＝x2（18﹣2x）＝﹣2x3+18x2，求导，得：V'＝﹣6x2+36x＝﹣6x（x﹣6），当0＜x＜6时，V是递增的，当x＞6时，V递减，则x＝6cm，18﹣2x＝6cm时，V的最大值是V＝216cm3故选：C．【点睛】本题考查四棱柱的体积，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题．14．【答案】C【解析】分析：先设速度为x千米/小时，再求出函数f(x)的表达式，再利用导数求其最小值.详解：当速度为x千米/小时时，时间为小时，所以f(x)=所以令当x∈（0,90）时，函数f(x)单调递减，当x∈（90,120）时，函数f(x)单调递增.所以x=90时，函数f(x)取得最小值.故答案为：C.点睛：（1）本题主要考查导数的应用，意在考查学生对这些知识的掌握水平和解决实际问题的能力.(2) 如果求函数在开区间内的最值，则必须通过求导，求函数的单调区间，最后确定函数的最值。15．【答案】A【解析】设是函数图像上两点的横坐标,则,且几何体的高为,半径为,由此可得,即,令,则,几何体的体积为,由于,令可得,故,应选A.考点：导数在实际生活中的运用．【易错点晴】本题重在考查导数在实际生活中的运用.解答本题时,先依据题设条件构建目标函数,进而确定函数的定义域,最后运用导数使得问题巧妙获解.值得强调的是,解答本题的关键是建构目标函数,目标函数中的变量是两个,然后利用纵坐标相等化为一个变量,进而借助换元法将变量进一步化为可导函数的变量,最后借助导数求出函数的最大值是本题获解.