高中苏教版 (2019)12.3 复数的几何意义授课ppt课件

12.3　复数的几何意义

知识点1　复数的几何意义

(1)复平面

建立直角坐标系来表示复数的平面叫作复平面，x轴叫作实轴，y轴叫作虚轴．

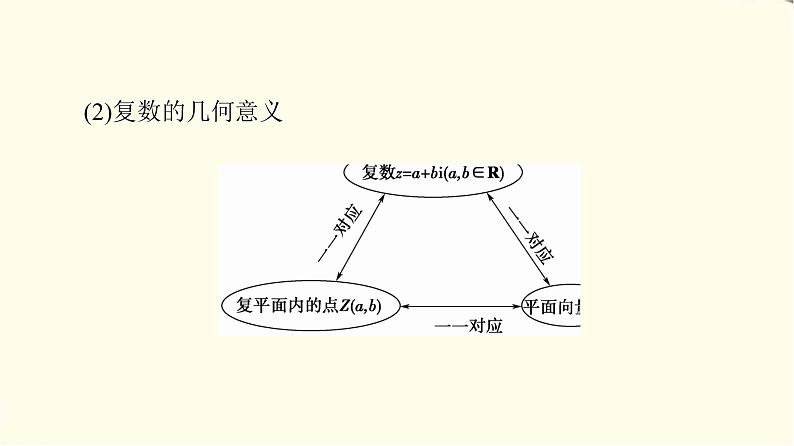
(2)复数的几何意义

1.思考辨析(正确的画“√”，错误的画“×”)

(1)在复平面内，对应于实数的点都在实轴上． (　　)

(2)在复平面内，虚轴上的点所对应的复数都是纯虚数． (　　)

[答案]　(1)√　(2)×

2.已知z1＝2＋i，z2＝1＋2i，则复数z＝z2－z1对应的点位于(　　)

A．第一象限   B．第二象限

C．第三象限   D．第四象限

B　[z＝z2－z1＝(1＋2i)－(2＋i)＝－1＋i，实部小于零，虚部大于零，故位于第二象限．]

知识点2　复数的模

(1)定义

向量的模叫作复数z＝a＋bi的模(或绝对值)，记作|z|或|a＋bi|.

(2)公式

|z|＝|a＋bi|＝.

(3)几何意义

复数z对应点Z到原点O的距离．

3.若z＝1＋2i，则||＝________.

　[∵z＝1＋2i，

∴|z|＝||＝.]

知识点3　复数加减法的几何意义

(1)如图所示，设向量，分别与复数z1＝a＋bi，z2＝c＋di对应，且，不共线，以，为两条邻边画▱OZ1ZZ2.则向量与复数z1＋z2相对应，向量与复数z1－z2相对应．

(2)|z1－z2|＝，即两个复数的差的模就是复平面内与这两个复数对应的两点间的距离．

类比绝对值|x－x0|的几何意义，|z－z0|(z，z0∈C)的几何意义是什么？

[提示]　|z－z0|(z，z0∈C)的几何意义是复平面内点Z到点Z0的距离．

4.复数4＋3i与－2－5i分别表示向量与，则向量表示的复数是________．

－6－8i　[因为复数4＋3i与－2－5i分别表示向量与，所以＝(4，3)，＝(－2，－5)，又＝－＝(－2，－5)－(4，3)＝(－6，－8)，所以向量表示的复数是－6－8i.]

类型1　复数的几何意义

【例1】　(1)实部为－2，虚部为1的复数所对应的点位于复平面的第________象限．

(2)设复数z＝(m∈R)在复平面内对应的点为Z.

①若点Z在虚轴上，求m的值；

②若点Z位于第一象限，求m的取值范围．

(1)二　[实部为－2，虚部为1的复数在复平面内对应的点为(－2，1)，位于第二象限．]

(2)[解]　z＝＝＝＋i.

①∵点Z在虚轴上，∴＝0，则m＝－2.

②点Z位于第一象限，则m＋2>0且1－2m>0，

解得－2<m<.

故实数m的取值范围是.

复数可由复平面内的点或向量进行表示

(1)复数与复平面内点的对应：复数的实、虚部是该点的横、纵坐标，利用这一点，可把复数问题转化为平面内点的坐标问题．

(2)复数与复平面内向量的对应：复数实、虚部是对应向量的坐标，利用这一点，可把复数问题转化为向量问题．

[跟进训练]

1．实数x取什么值时，复平面内表示复数z＝x2＋x－6＋(x2－2x－15)i的点Z.

(1)位于第三象限；(2)位于第四象限；(3)位于直线x－y－3＝0上．

[解]　因为x是实数，所以x2＋x－6，x2－2x－15也是实数．

(1)当实数x满足即－3＜x＜2时，点Z位于第三象限．

(2)当实数x满足

即2＜x＜5时，点Z位于第四象限，

(3)当实数x满足(x2＋x－6)－(x2－2x－15)－3＝0，即3x＋6＝0，x＝－2时，点Z位于直线x－y－3＝0上．

类型2　复数加减法的几何意义

【例2】　(1)向量对应的复数为1＋4i，向量对应的复数为－3＋6i，则向量＋对应的复数为________．

(2)若，对应的复数分别是7＋i，3－2i，则||＝________.

(1)－2＋10i　(2)5　[(1)(1＋4i)＋(－3＋6i)＝－2＋10i.即向量＋对应的复数为－2＋10i.

(2)对应复数为(3－2i)－(7＋i)＝－4－3i，

∴||＝|－4－3i|＝＝5.]

1．根据复数加减运算的几何意义可以把复数的加减运算转化为向量的坐标运算，同样满足三角形和平行四边形法则．

2．复数加减运算的几何意义为应用数形结合思想解决复数问题提供了可能．

[跟进训练]

2．在复平面内，A，B，C分别对应复数z1＝1＋i，z2＝5＋i，z3＝3＋3i，以AB，AC为邻边作一个平行四边形ABDC，求D点对应的复数z4及AD的长．

[解]　由复数加减法几何意义：

对应复数z3－z1，对应复数z2－z1，

对应复数z4－z1，

根据向量的平行四边形法则，得＝＋，

∴z4－z1＝(z2－z1)＋(z3－z1)，

∴z4＝z2＋z3－z1＝(5＋i)＋(3＋3i)－(1＋i)＝7＋3i，

∴AD的长为||＝|z4－z1|

＝|(7＋3i)－(1＋i)|＝|6＋2i|＝2.

类型3　复数的模及其几何意义

【例3】　(1)如果复数z满足|z＋i|＋|z－i|＝2，那么|z＋i＋1|的最小值是(　　)

A．1  B．  C．2  D．

(2)若复数z满足|z＋＋i|≤1，求|z|的最大值和最小值．

结合|z|的几何意义，思考分别满足|z＋i|＋|z－i|＝2及|z＋＋i|≤1的复数z所对应点的轨迹，进而数形结合求得相应结果.

(1)A　[设复数－i，i，－1－i在复平面内对应的点分别为Z1，Z2，Z3，因为|z＋i|＋|z－i|＝2， |Z1Z2|＝2，所以点Z的集合为线段Z1Z2.

问题转化为：动点Z在线段Z1Z2上移动，求|ZZ3|的最小值，因为|Z1Z3|＝1，

所以|z＋i＋1|min＝1.]

(2)[解]　如图所示， ||＝＝2.

所以|z|max＝2＋1＝3，|z|min＝2－1＝1.

|z1－z2|表示复平面内z1，z2对应的两点间的距离.利用此性质，可把复数模的问题转化为复平面内两点间的距离问题，从而进行数形结合，把复数问题转化为几何图形问题求解.

[跟进训练]

3．设z∈C，且|z＋1|－|z－i|＝0，则|z＋i|的最小值为(　　)

A．0  B．1  C．  D．

C　[由|z＋1|＝|z－i|知，在复平面内，复数z对应的点的轨迹是以(－1，0)和(0，1)为端点的线段的垂直平分线，即直线y＝－x，而|z＋i|表示直线y＝－x上的点到点(0，－1)的距离，其最小值等于点(0，－1)到直线y＝－x的距离，即为.]

1．已知i为虚数单位，若z1＝2＋i，z2＝3＋ai(a∈R)，且z1＋z2在复平面内所对应的点在实轴上，则a的值为(　　)

A．3  B．2  C．1  D．－1

D　[因为z1＋z2＝5＋(a＋1)i，由题意可知a＋1＝0，∴a＝－1，故选D.]

2．已知复数z在复平面内对应的点为Z(2，－1)，则(　　)

A．z＝－1＋2i   B．|z|＝5

C．z是纯虚数   D．z＝2－i

D　[因为复数z在复平面内对应的点为Z(2，－1)，则z＝2－i，所以|z|＝＝，z不是纯虚数，所以A、B、C不正确，D正确．故选D.]

3．设复数z满足|z－i|＝1，z在复平面内对应的点为(x，y)，则(　　)

A．(x＋1)2＋y2＝1   B．(x－1)2＋y2＝1

C．x2＋(y－1)2＝1   D．x2＋(y＋1)2＝1

C　　[法一：∵z在复平面内对应的点为(x，y)，∴z＝x＋yi(x，y∈R)．∵|z－i|＝1，∴|x＋(y－1)i|＝1，∴x2＋(y－1)2＝1.故选C.

法二：∵|z－i|＝1表示复数z在复平面内对应的点(x，y)到点(0，1)的距离为1，∴x2＋(y－1)2＝1.故选C.]

4．复数z＝x－2＋(3－x)i在复平面内的对应点在第四象限，则实数x的取值范围是________．

(3，＋∞)　[∵复数z在复平面内对应的点在第四象限，

∴解得x＞3.]

5．已知复数z满足z＋|z|＝2＋8i，则复数z＝________.

－15＋8i　[设z＝a＋bi(a，b∈R)，

则|z|＝，

代入方程得，a＋bi＋＝2＋8i，

∴解得∴z＝－15＋8i.]

回顾本节知识，自我完成以下问题：

1．复数z＝a＋bi(a，b∈R)，复平面内的点Z(a，b)及平面向量之间存在怎样的关系？

[提示]　

2．复数|z1－z2|的几何意义是什么？

[提示]　复数|z1－z2|表示复数z1，z2对应两点Z1与Z2间的距离．

3．|z1z2|与|z1||z2|存在怎样的关系？

[提示]　|z1z2|＝|z1||z2|.

利用复数产生分形图

以前我们学过的函数，定义域都是实数集的子集．但函数概念还可以推广：定义域是复数集的子集的函数称为复变函数．类似地，我们还可以得到多项式复变函数的概念．例如，f(z)＝z2就是一个多项式复变函数，此时

f(i)＝i2＝－1，f(1＋i)＝(1＋i)2＝2i.

给定多项式复变函数f(z)之后，对任意一个复数z0，通过计算公式zn＋1＝f(zn)，n∈N可以得到一列值

z0，z1，z2，…，zn，….

如果存在一个正数M，使得|zn|<M对任意n∈N都成立，则称z0为f(z)的收敛点；否则，称z0为f(z)的发散点．f(z)的所有收敛点组成的集合称为f(z)的充满茹利亚集．

例如，当f(z)＝z2时，如果z0＝i，则得到的一列值是

i，－1，1，1，…，1，…；

如果z0＝1＋i，则算出的一列值是

1＋i，2i，－4，…，2，….

显然，对于f(z)＝z2来说，i为收敛点，1＋i为发散点．事实上，利用|z2|＝|z|2可以证明，f(z)＝z2的充满茹利亚集是一个单位圆盘(即由满足|z|≤1的所有z组成的集合)．

让人惊讶的是，当f(z)＝z2＋c时，对于某些复数c来说，f(z)的充满茹利亚集是非常复杂的．如果利用计算机对不同形态的收敛点和发散点进行不同的着色，就可以得到分形图．而且，如果按照一定的规则对c进行分类，并进行着色，可以得到如图所示的芒德布罗分形图．