高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用图片ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用图片ppt课件，共34页。PPT课件主要包含了探索新知，点到直线的距离，点到平面的距离，平行平面间的距离，异面直线间的距离，巩固练习，知识点，课堂小结等内容，欢迎下载使用。
我们知道，立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等 . 如何用空间向量解决这些距离问题呢？
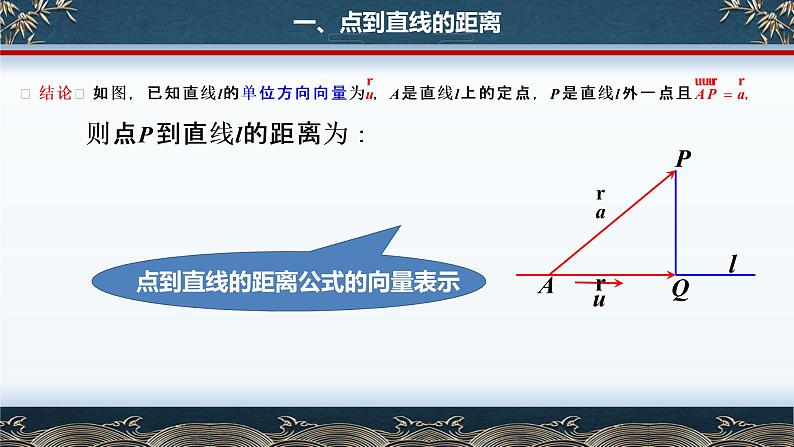
下面我们先研究用向量方法求直线外一点P到直线l 的距离．
例1 在长方体OABC－O1A1B1C1中，OA＝2，AB＝3，AA1＝2，求O1到直线AC的距离.
解 连接AO1，建立如图所示的空间直角坐标系，则A(2,0,0)，O1(0,0,2)，C(0,3,0)，
【悟】向量法求点线距的一般步骤
(4) 另外，注意平行直线间的距离与点到直线的距离之间的转化.
解　如图，分别以AB，AD，AP所在直线为x，y，z轴建立空间直角坐标系，
【练1】如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB＝3,AD＝4， PA＝1，求点P到BD的距离.
则P(0,0,1)，B(3,0,0)，D(0,4,0)，
揭秘：在其中一条直线上取定一点，则该点到另一条直线的距离即为两 条平行直线之间的距离.
【拓展】类比点到直线的距离的求法，如何求两条平行直线之间的距离？
【思考】已知平面α的法向量为n，A是平面α内的定点，P是平面α外一点.如何求平 面α外一点P到平面α的距离？
揭秘　过点P作平面α的垂线l，交平面α于点Q，
二、点到平面的距离与直线到平面的距离
(2)如果一条直线l与一个平面α平行，可在直线l上任取一点P，求点P 到平面α的距离即可.
(3)如果两个平面α，β互相平行，其中一个平面α内任取一点P，求点P到平面β的距离即可.
例3 如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD＝1，E,F分别为AB，BC的中点. (1)求点D到平面PEF的距离； (2)求直线AC到平面PEF的距离
解（2）由题意得，AC∥EF，从而直线AC//平面PEF
所以直线AC到平面PEF的距离为：直线AC上任意一点到平面PEF的距离，
不妨设直线AC到平面PEF的距离即为点A到平面PEF的距离，
【悟】向量法求点面距离的步骤
解　设正四棱柱的高为h(h>0)，建立如图所示的空间直角坐标系，
设平面AB1D1的法向量为n＝(x，y，z)，
取z＝1，得n＝(h，h，1)，
故正四棱柱ABCD－A1B1C1D1的高为2.
有A(0,0，h)，B1(1,0,0)，D1(0,1,0)，C(1，1，h)，
【问题】 如何求平行平面间的距离？
【问题】如何求两条异面直线的距离？
三、平行平面、异面直线间的距离
若两个平面平行，在其中一个平面上的任意一点到另一个平面的距离都相等，即为平行平面间的距离。
求平行平面间的距离的方法
（1)在其中一个平面上任取定一点P， (2)求点P到另一平面的距离
例4 已知棱长为1的正方体ABCD－A1B1C1D1，求平面AB1C与平面A1C1D之间的距离
解 建立如图所示的空间直角坐标系，
则A1(1,0,0)，C1(0,1,0)，D(0，0,1)，A(1,0,1)，
设平面A1C1D的一个法向量为m＝(x，y，1)，
故m＝(1,1,1)，显然平面AB1C∥平面A1C1D，
两条异面直线a,b,作b///b,且b/∩a=, b/与确定一个平面ɑ， b//平面ɑ，则， b到平面ɑ的距离就是两条异面直线a,b间的距离。
求异面直线间的距离的方法
例5. 如图，在三棱柱ABC－A1B1C1中，所有棱长均为1，且AA1⊥底面ABC，O是AC1与A1C的交点， 求异面直线A1B1与BO间的距离.
解（法一） 连结BC1, 建立如图所示的空间直角坐标系，
设平面ABC1的一个法向量为n＝(x，y，1)，
解（法二） 建立如图所示的空间直角坐标系，
1.已知直线l经过点A(2,3,1)，且向量n＝(1,0，－1)所在直线与l垂直，则点P(4,3,2)到l 的距离为____.
解 以O为坐标原点，建立如图所示的空间直角坐标系.由题意可知A(1,0,0)，B(0,2,0)，C(0,0,2)，
则B1(2,2,0)，C1(0,2,0)，E(2,1，2)，F(1,2,2).
设平面B1EF的法向量为n＝(x，y，z)，
令z＝1，得n＝(2,2,1).
因为B1C1∥平面A1BCD1，
5.在我国古代数学名著《九章算术》中，将四个面都为直角三角形的三棱锥称为鳖臑(bie na)，如图,已知 在鳖臑P－ABC中，PA⊥平面ABC，PA＝AB＝BC＝2，M为PC的中点，则点P到平面MAB的距离为_______.
解 以B为坐标原点，BA，BC所在直线分别为x轴、y轴建立空间直角坐标系，
设n＝(x，y，z)为平面ABM的一个法向量，
(1)点到直线的距离.
(2)点到平面的距离与直线到平面的距离.
2.方法归纳：数形结合、转化法.
3.易错点：对距离公式理解不到位，在使用时生硬套用.
课本P35 练习 1，2，3