初中数学鲁教版 (五四制)九年级上册7 二次函数与一元二次方程一等奖教案

《二次函数与一元二次方程》教学设计

一、 教学目标

(一)教学知识点

1.经历探索二次函数与一元二次方程的关系的过程，体会方程与函数之间的联系。
  2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，理解何时方程有两个不等的实根、两个相等的实数和没有实根。
  3.理解一元二次方程的根就是二次函数与y=h(h是实数)交点的横坐标。

(二)能力训练要求
  1.经历探索二次函数与一元二次方程的关系的过程，培养学生的探索能力和创新精神。
  2.通过观察二次函数图象与x轴的交点个数，讨论一元二次方程的根的情况,进一步培养学生的数形结合思想。
  3.通过学生共同观察和讨论，培养大家的合作交流意识。
  (三)情感与价值观要求
  1.经历探索二次函数与一元二次方程的关系的过程,体验数学活动充满着探索与创造，感受数学的严谨性以及数学结论的确定性。
  2.具有初步的创新精神和实践能力。

二、 教学重点
  1.体会方程与函数之间的联系。
  2.理解何时方程有两个不等的实根，两个相等的实数和没有实根。
  3.理解一元二次方程的根就是二次函数与y=h(h是实数)交点的横坐标。

三、 教学难点
  1.探索方程与函数之间的联系的过程。
  2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系。
四、 教学方法

     讨论探索法
五、教学过程

（一）创设问题情境，引入新课
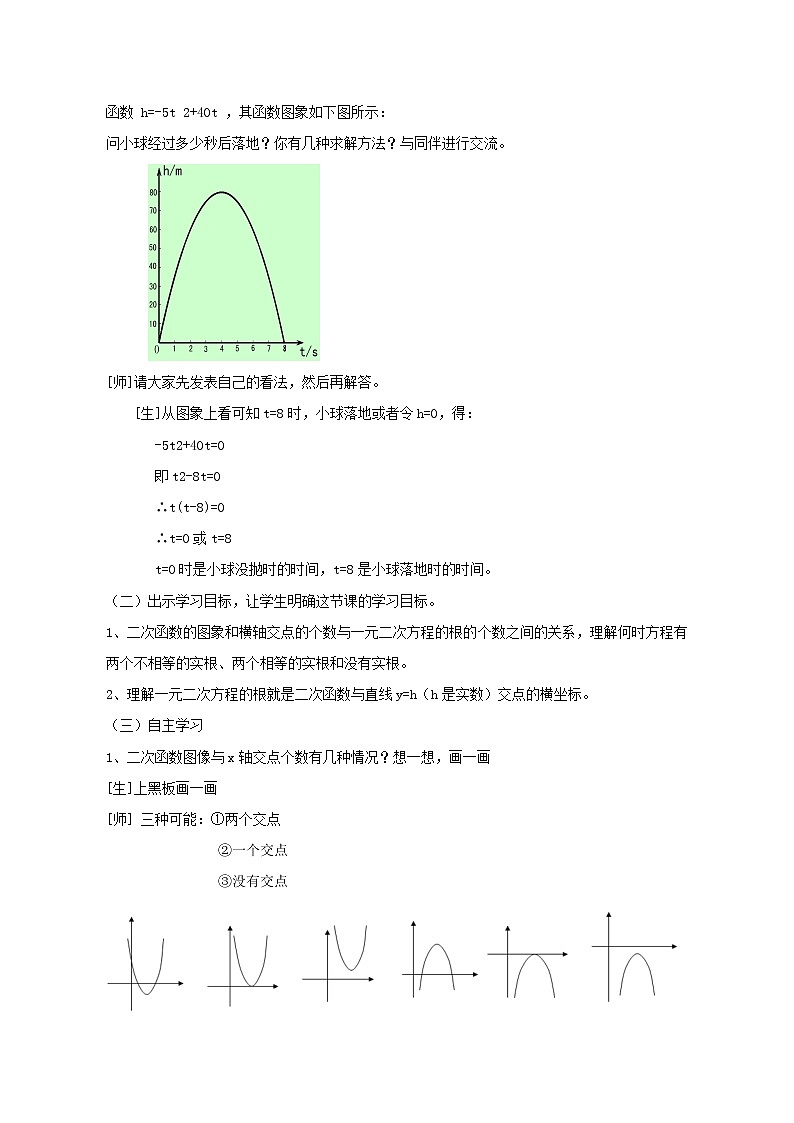
  一个小球以一定的速度竖直向上抛起，小球的高度h(m)与运动时间t(s)之间的关系为二次函数 h=-5t 2+40t ，其函数图象如下图所示： 

问小球经过多少秒后落地？你有几种求解方法？与同伴进行交流。

[师]请大家先发表自己的看法，然后再解答。
  [生]从图象上看可知t=8时，小球落地或者令h=0，得：
    -5t2+40t=0
    即t2-8t=0
    ∴t(t-8)=0
    ∴t=0或t=8
    t=0时是小球没抛时的时间，t=8是小球落地时的时间。

（二）出示学习目标，让学生明确这节课的学习目标。

1、二次函数的图象和横轴交点的个数与一元二次方程的根的个数之间的关系，理解何时方程有两个不相等的实根、两个相等的实根和没有实根。

2、理解一元二次方程的根就是二次函数与直线y=h（h是实数）交点的横坐标。

（三）自主学习 

1、二次函数图像与x轴交点个数有几种情况？想一想，画一画

[生]上黑板画一画

[师] 三种可能：①两个交点        

                ②一个交点

                ③没有交点

（四）合作探究

二次函数①y=x2+2x, ②y=x2-2x+1, ③y=x2-2x+2的图象如下图所示：

(1)每个图象与x轴有几个交点？

(2)一元二次方程x2+2x=0,x2-2x+1=0有几个根？用判别式验证一下:一元二次方程x2-2x+2=0有根吗？

(3)二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系？

[师]同学们先自主完成后再小组讨论。

展示交流：

[生](1)二次函数y=x2+2x，y=x2-2x+1，y=x2-2x+2的图象与x轴分别有两个交点，一个交点，没有交点。

(2)一元二次方程x2+2x=0有两个根0，-2；方程x2-2x+1=0有两个相等的根1或一个根1；方程x2-2x+2=0没有实数根。

(3)从观察图象和讨论中可知，二次函数y=x2+2x的图象与x轴有两个交点，交点的坐标分别为(0,0)，(-2,0),方程x2+2x=0有两个根0,-2；

 二次函数y=x2-2x+1的图象与x轴有一个交点,交点坐标为(1,0)，方程x2-2x+1=0有两个相等的实数根(或一个根)1；二次函数y=x2-2x+2的图象与x轴没有交点，方程x2-2x+2=0没有实数根。

由此可知，二次函数y=ax2+bx+c的图象和x轴交点的横坐标即为一元二次方程ax2+bx+c=0的根。

[师]大家总结得非常棒  

（五）跟踪练习一

1．若方程ax2+bx+c=0的根为x1=-2和x2=3，则二次函数y=ax2+bx+c的图象与x轴交点坐标是                             。

2.抛物线y=x2-4x+4与x轴有     个交点，交点坐标是 　　　　　　　　。                 

3.抛物线y=0.5x2-x+3与x轴的交点情况是（      ）

    A 两个交点   B 一个交点   C 没有交点   D 画出图象后才能说明

4 .不画图象，求抛物线y=x2-3x-4与x轴的交点坐标。

5.若函数y=mx2-6x+1图象与x 轴是只有一个公共点，求m的值。

[师]4、5题学生好黑板做。

（六）能力升华

1、 一元二次方程x2-4x+4=0的根是函数 y=x2-4x+4的图象与（          ）交点的横坐标。

2、一元二次方程x2-4x+4=1的根是二次函数y=x2-4x+4的图象与（                  ）交点坐标的横坐标 。

（七）跟踪练习二

函数的图象y=ax2+bx+c如图所示， 那么

(1)关于ax2+bx+c=0的一元二次方程的根的情况是(                    )

(2)关于ax2+bx+c=4的一元二次方程的根的情况是(                    )

(3)关于ax2+bx+c=2的一元二次方程的根的情况是(                    )

（八）跟踪练习三

二次函数y＝x2－2x－3和一次函数y＝x＋2有交点吗？有几个？

（九）跟踪练习四

    已知抛物线经过点M（0，2），且方程ax2+bx+c=0的两个根为x1=-1,x2=2,求抛物线的解析式？

在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?

[师]请大家讨论解决.

[生]在式子h=-5t2+40中，当h0=0时

 -5t2+40t=60
   t2-8t+12=0
   ∴t=2或t=6
   因此当小球离开地面2秒和6秒时,高度都是60m。

（十）课堂小结

[师]请同学们回顾一下，这节课都有哪些收获。

（十一）堂清检测 

（十二）作业：练习册p