2019年广东省东莞市莞城区可园中学中考二模数学试卷

这是一份2019年广东省东莞市莞城区可园中学中考二模数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. −12 的倒数为
A. −2B. 12C. −12D. 2

2. 六个大小相同的正方体搭成的几何体如图所示，其俯视图是( )
A. B.
C. D.

3. 习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约 11700000 人，将数据 11700000 用科学记数法表示为
A. 1.17×107B. 11.7×106C. 0.117×107D. 1.17×108

4. 下列所述图形中，是轴对称图形但不是中心对称图形的是
A. 圆B. 菱形C. 平行四边形D. 等腰三角形

5. 下列运算正确的是
A. 3a+2b=5abB. a3⋅a2=a6C. a3÷a2=aD. 3a2=3a2

6. 某体育用品商店一天中卖出某种品牌的运动鞋 15 双，其中各种尺码的鞋的销售量如表所示：
鞋的尺码销售量/双13362
则这 15 双鞋的尺码组成的一组数据中，众数和中位数分别为
A. 24.5，24.5B. 24.5，24C. 24，24D. 23.5，24

7. 点 P1,−2 关于 x 轴对称的点的坐标是
A. −1,2B. −2,1C. −1,−2D. 1,2

8. 如图，在 △ABC 中，CD 平分 ∠ACB 交 AB 于点 D，过点 D 作 DE∥BC 交 AC 于点 E．若 ∠A=54∘，∠B=48∘，则 ∠CDE 的大小为
A. 44∘B. 40∘C. 39∘D. 38∘

9. 若一元二次方程 x2−4x+m=0 有两个不相同的实数根，则实数 m 的取值范围是
A. m≥4B. m≤4C. m>4D. m<4

10. 如图，在平行四边形 ABCD 中，AB=6，BC=10，AB⊥AC，点 P 从点 B 出发沿着 B→A→C 的路径运动，同时点 Q 从点 A 出发沿着 A→C→D 的路径以相同的速度运动，当点 P 到达点 C 时，点 Q 随之停止运动，设点 P 运动的路程为 x，y=PQ2，下列图象中大致反映 y 与 x 之间的函数关系的是
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 函数 y=3x−1 中，自变量 x 的取值范围是 ．

12. 分解因式：2a2−4a+2= ．

13. 如图，已知 AB 是 ⊙O 的直径，AB=2，C，D 是圆周上的点，且 ∠CDB=30∘，则 BC 的长为 ．

14. 一个多边形的每一个外角为30∘，那么这个多边形的边数为 ．

15. 已知 4a+3b=1，则整式 8a+6b−3 的值为 ．

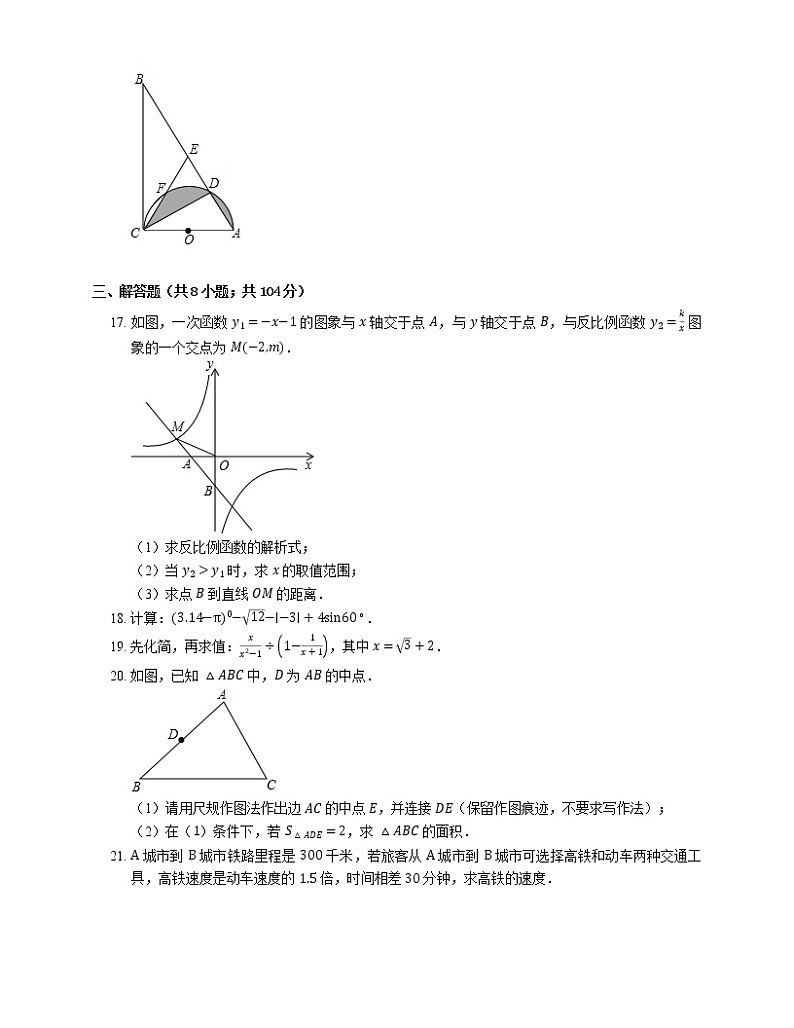
16. 如图，Rt△ABC 中，∠ACB=90∘，∠B=30∘，AB=12 cm，以 AC 为直径的半圆 O 交 AB 于点 D，点 E 是 AB 的中点，CE 交半圆 O 于点 F，则图中阴影部分的面积为 cm2．

三、解答题（共8小题；共104分）
17. 如图，一次函数 y1=−x−1 的图象与 x 轴交于点 A，与 y 轴交于点 B，与反比例函数 y2=kx 图象的一个交点为 M−2,m．
（1）求反比例函数的解析式；
（2）当 y2>y1 时，求 x 的取值范围；
（3）求点 B 到直线 OM 的距离．

18. 计算：3.14−π0−12−−3+4sin60∘．

19. 先化简，再求值：xx2−1÷1−1x+1，其中 x=3+2．

20. 如图，已知 △ABC 中，D 为 AB 的中点．
（1）请用尺规作图法作出边 AC 的中点 E，并连接 DE（保留作图痕迹，不要求写作法）；
（2）在（1）条件下，若 S△ADE=2，求 △ABC 的面积．

21. A 城市到 B 城市铁路里程是 300 千米，若旅客从 A 城市到 B 城市可选择高铁和动车两种交通工具，高铁速度是动车速度的 1.5 倍，时间相差 30 分钟，求高铁的速度．

22. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样，便捷．某校数学兴趣小组设计了一份调查问卷，要求每人选且只选一种你最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题．
（1）这次活动共调查了 人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为 ；将条形统计图补充完整．
（2）如果某个社区共有 3000 个人，那么选择微信支付的人约有 ；
（3）在一次购物中，小明和小亮都想从“微信”、“支付宝”、”银行卡”三种支付方式中选一种方式，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．

23. 已知：如图，平行四边形 ABCD，对角线 AC 与 BD 相交于点 E，点 G 为 AD 的中点，连接 CG，CG 的延长线交 BA 的延长线于点 F，连接 FD．
（1）求证：AB=AF；
（2）若 AG=AB，∠BCD=120∘，判断四边形 ACDF 的形状，并证明你的结论．

24. 如图 1，在直角 △ABC 中，∠ACB=90∘，AO 是 △ABC 的角平分线，以 O 为圆心，OC 为半径作圆 O．
（1）求证：AB 是 ⊙O 的切线；
（2）已知 AO 交圆 O 于点 E，延长 AO 交圆 O 于点 D，tan∠D=12，求 AEAC 的值；
（3）如图 2，在（2）条件下，若 AB 与 ⊙O 的切点为点 F，连接 CF 交 AD 于点 G，设 ⊙O 的半径为 3，求 CF 的长．
答案
第一部分
1. A【解析】−12 的倒数为 −2．
2. B【解析】【分析】俯视图有3列，从左到右正方形个数分别是2，1，2．
【解析】解：俯视图从左到右分别是2，1，2个正方形，如图所示：．
故选：B．
【点评】本题考查了简单组合体的三视图，培养学生的思考能力和对几何体三种视图的空间想象能力．
3. A【解析】11700000=1.17×107．
4. D
5. C
【解析】A．3a+2b，无法计算，故此选项错误；
B．a3⋅a2=a5，故此选项错误；
C．a3÷a2=a，正确；
D．3a2=9a2，故此选项错误．
6. A【解析】这组数据中，众数为 24.5，中位数为 24.5．
7. D【解析】点 Pm,n 关于 x 轴对称点的坐标 Pʹm,−n，
∴ 点 P1,−2 关于 x 轴对称的点的坐标为 1,2．
8. C【解析】∵∠A=54∘，∠B=48∘，
∴∠ACB=180∘−54∘−48∘=78∘，
∵CD 平分 ∠ACB 交 AB 于点 D，
∴∠DCB=12×78∘=39∘，
∵DE∥BC，
∴∠CDE=∠DCB=39∘．
9. D【解析】∵ 一元二次方程 x2−4x+m=0 有两个不相同的实数根，
∴Δ=16−4m>0，解得 m<4．
10. B
【解析】在 Rt△ABC 中，∠BAC=90∘，AB=6，BC=10，
∴AC=BC2−AB2=8．
当 0≤x≤6 时，AP=6−x，AQ=x，
∴y=PQ2=AP2+AQ2=2x2−12x+36；
当 6≤x≤8 时，AP=x−6，AQ=x，
∴y=PQ2=AQ−AP2=36；
当 8≤x≤14 时，CP=14−x，CQ=x−8，
∴y=PQ2=CP2+CQ2=2x2−44x+260．
第二部分
11. x≥13
【解析】由题意得 3x−1≥0，解得 x≥13．
12. 2a−12
【解析】原式=2a2−2a+1=2a−12.
13. 1
【解析】∵AB 是直径，
∴∠ACB=90∘，
∵∠A=∠CDB=30∘，
∴BC=12AB=1．
14. 12
【解析】【分析】一个正多边形的每个内角都相等，根据内角与外角互为邻补角，因而就可以求出外角的度数．根据任何多边形的外角和都是360∘，利用360∘除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．
【解析】解：多边形的边数：360∘÷30∘=12，
则这个多边形的边数为12．
故答案为：12．
【点评】根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．
15. −1
【解析】∵4a+3b=1，
∴8a+6b=2，8a+6b−3=2−3=−1．
16. 3π−934
【解析】∵Rt△ABC 中，∠ACB=90∘，∠B=30∘，AB=12 cm，
∴AC=12AB=6 cm，∠A=60∘．
∵E 是 AB 的中点，
∴CE=12AB，则 △ACE 是等边三角形．
∴∠BCE=90∘−60∘=30∘，
∵AC 是直径，
∴∠CDA=90∘，
∴∠ACD=90∘−∠A=30∘，
∴∠BCE=∠ACD，
∴CF=AD，
连接 OD，作 OG⊥CD 于点 G，
则 ∠COD=120∘，OG=12OC=32，CG=12CD=332．
∴ 阴影部分的面积为：S扇形COD−S△COD=120π×32360−12×32×33=3π−934．
第三部分
17. （1） 把 M−2,m 代入 y=−x−1 得 m=2−1=1，则 M−2,1，
把 M−2,1 代入 y=kx 得 k=−2×1=−2，
∴ 反比例函数解析式为 y=−2x．
（2） 解方程组 y=−2x,y=−x−1 得 x=−2,y=1 或 x=1,y=−2,
则反比例函数与一次函数的另一个交点坐标为 1,−2，
当 −21 时，y2>y1．
（3） OM=12+22=5，S△OMB=12×1×2=1，
设点 B 到直线 OM 的距离为 h，12⋅5⋅h=1，解得 h=255，
即点 B 到直线 OM 的距离为 255．
18. 3.14−π0−12−−3+4sin60∘=1−23−3+23=−2.
19. 原式=xx+1x−1÷x+1−1x+1=xx+1x−1⋅x+1x=1x−1.
当 x=3+2 时，
原式=13+2−1=13+1=3−12.
20. （1） 如图所示，DE 即为所求．
（2） ∵D 是 AB 中点，E 是 AC 中点，
∴DE 是 △ABC 的中位线．
∴DE∥BC 且 DEBC=12．
∴△ADE∽△ABC，则 S△ADES△ABC=DEBC2=14．
又 S△ADE=2，
∴S△ABC=8．
21. 设动车速度为 x 公里/小时，则高铁速度为 1.5x 公里/小时．
依题意，得：
300x−3001.5x=12.
解得：
x=200.
经检验，x=200 是原分式方程的根，且符合题意．
∴1.5x=300．
答：高铁速度为 300 公里/小时．
22. （1） 200；81∘
补全图形如下：
【解析】这次活动共调查了 45+50+15÷1−15%−30%=200（人），
在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为 360∘×45200=81∘，
微信的人数为 200×30%=60（人），银行卡的人数为 200×15%=30（人）．
（2） 900 人
【解析】选择微信支付的人约有 3000×30%=900（人）．
（3） 将微信记为 A 、支付宝记为 B 、银行卡记为 C，
画树状图如下：
∵ 共有 9 种等可能的结果，其中两人恰好选择同一种支付方式的有 3 种，
∴ 两人恰好选择同一种支付方式的概率为 39=13．
23. （1） ∵ 四边形 ABCD 是平行四边形，
∴AB∥CD，AB=CD，
∴∠AFC=∠DCG，
∵GA=GD，∠AGF=∠CGD，
∴△AGF≌△DGC，
∴AF=CD，
∴AB=AF．
（2） 结论：四边形 ACDF 是矩形．
理由：
∵AF=CD，AF∥CD，
∴ 四边形 ACDF 是平行四边形，
∵ 四边形 ABCD 是平行四边形，
∴∠BAD=∠BCD=120∘，
∴∠FAG=60∘，
∵AB=AG=AF，
∴△AFG 是等边三角形，
∴AG=GF，
∵△AGF≌△DGC，
∴FG=CG，
∵AG=GD，
∴AD=CF，
∴ 四边形 ACDF 是矩形．
24. （1） 如图，过点 O 作 OF⊥AB 于点 F．
∵AO 平分 ∠CAB，OC⊥AC，OF⊥AB，
∴OC=OF，
∴AB 是 ⊙O 的切线．
（2） 如图，连接 CE．
∵ED 是 ⊙O 的直径，
∴∠ECD=90∘．
∴∠ECO+∠OCD=90∘．
∵∠ACB=90∘，
∴∠ACE+∠ECO=90∘，
∴∠ACE=∠OCD，
∵OC=OD，
∴∠OCD=∠ODC，
∴∠ACE=∠ODC，
∵∠CAE=∠CAE，
∴△ACE∽△ADC，
∴AEAC=CECD，
∵tan∠D=CECD=12，
∴AEAC=12．
（3） 由（2）可知：AEAC=12，
∴ 设 AE=x，AC=2x，
∵△ACE∽△ADC，
∴AEAC=ACAD，
∴AC2=AE⋅AD，
∴2x2=xx+6，解得：x=2 或 x=0（不合题意，舍去），
∴AE=2，AC=4，
∴AO=AE+OE=2+3=5，
如图，连接 CF 交 AD 于点 M，
∵AC，AF 是 ⊙O 的切线，
∴AC=AF，∠CAO=∠OAF，
∴CF⊥AO，
∴∠ACO=∠CMO=90∘，
∵∠COM=∠AOC，
∴△CMO∽△ACO，
∴OCOM=OAOC，
∴OC2=OM⋅OA，
∴OM=95，
∴CM=OC2−OM2=32−952=125，
∴CF=2CM=245．