初中2 求解二元一次方程组图片ppt课件

这是一份初中2 求解二元一次方程组图片ppt课件，共18页。PPT课件主要包含了学习目标，课时讲解，课时流程，课时导入，基本思路，写出方程组的解，消元二元，知识点，直接加减消元，感悟新知等内容，欢迎下载使用。
直接加减消元先变形，再加减消元解方程组的应用
主要步骤：
把变形后的方程代入到另一个方程中，消去一个元
分别求出两个未知数的值
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
1、解二元一次方程组的基本思路是什么？
2、用代入法解方程的步骤是什么？
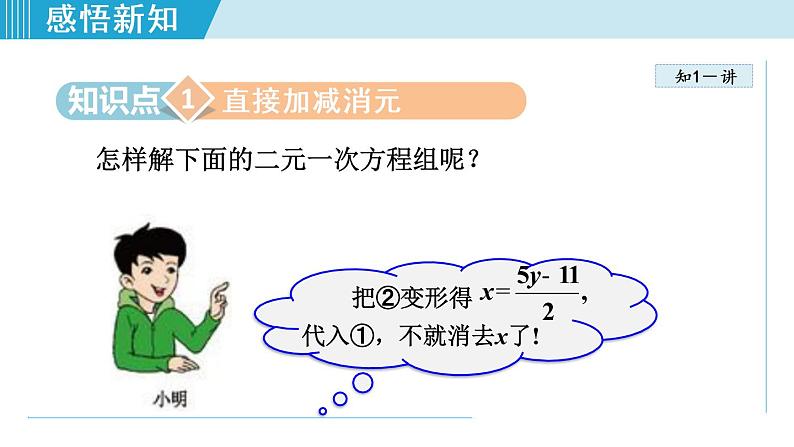
把②变形得 代入①，不就消去x了!
怎样解下面的二元一次方程组呢？
按小丽的思路，你能消去一个未知数吗?
把②变形得5y＝2x＋11, 可以直接代入①呀！
5y和－5y互为相反数……
两个方程相加，可以得到 5x = 10, x = 2. 将x = 2代入①，得 6 + 5y = 21， y = 3.所以方程组
　加减消元法的定义：通过将两个方程相加（减）消去其中一个未知数，将二元一次方程组转化为一元一次方程来解，这种解二元一次方程组的方法叫做加减消元法，简称加减法．
特别解读1.两个方程同一未知数的系数的绝对值相等或成倍数关系时，解方程组应考虑用加减消元法.2. 如果同一未知数的系数的绝对值既不相等又不成倍数关系，我们应设法将一个未知数的系数的绝对值转化为相等关系.3. 用加减法时，一般选择系数比较简单（同一未知数的系数的绝对值相等或成倍数关系）的未知数作为消元对象.
解方程组：解：②－①，得 8y＝－ 8， y＝－1. 将y＝－1代入①，得2x+5＝7， x＝1. 所以原方程组的解是
用消元法解二元一次方程组的步骤：(1)消元：若方程组中某一个未知数的系数相等或 相反，利用减法或加法消去一个未知数.(2)求解：得到一个未知数的值.(3)回代：求另一个未知数的值.(4)写出解.
解方程组：
能否使两个方程中x(或y)的系数相等(或相反)呢?
解：①×3，得6x+9y＝36， ③ ②×2，得6x+8y＝34， ④ ③－④，得 y＝2. 将y＝2代入①,得 x＝3. 所以原方程组的解是
(1)两个方程同一未知数的系数的绝对值相等或成 倍数关系时，解方程组应考虑用加减消元法． (2)如果同一未知数的系数的绝对值既不相等又不成 倍数关系，我们应设法将一个未知数的系数的绝 对值转化为相等关系． (3)用加减法时，一般选择系数比较简单(同一未知数 的系数的绝对值相等或成倍数关系)的未知数作为 消元对象．
用加减法解方程组：导引：方程组的两个方程中，y的系数的绝对值成倍数 关系，方程②乘3就可与方程①相加消去y.解： ②×3，得 51x－9y＝222，③ ①＋③，得 59x＝295，解得 x＝5. 把x＝5代入①，得8×5＋9y＝73，解得 所以原方程组的解为
用加减法解方程组：导引：方程①和②中，x，y的系数的绝对值都不相等 又不成倍数关系，应取系数的绝对值的最小公 倍数6，可以先消去x，也可以先消去y.
解：①×3，得6x＋9y＝9.③ ②×2，得6x＋4y＝22.④ ③－④，得5y＝－13，即 把 所以这个方程组的解为
方程组中任意一个未知数的系数的绝对值既 不相等又不成倍数关系，可利用最小公倍数的知 识，给两个方程都适当地乘一个数，使某个未知 数的系数的绝对值相等.