2020-2021学年2.3.1向量数量积的物理背景与定义课后练习题

展开

这是一份2020-2021学年2.3.1向量数量积的物理背景与定义课后练习题，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．若a·c＝b·c(c≠0)，则( )
A．a＝b
B．a≠b
C．|a|＝|b|
D．a在c方向上的正射影的数量与b在c方向上的正射影的数量必相等
[答案] D
[解析] ∵a·c＝b·c，
∴|a|·|c|cs＝|b|·|c|cs，
即|a|cs＝|b|cs，故选D．
2．已知a、b为两个单位向量，则下列说法正确的是( )
A．a＝b B．如果a∥b，那么a＝b
C．a·b＝1 D．a2＝b2
[答案] D
[解析] ∵a、b为两个单位向量，
∴|a|＝|b|＝1.
∴a2＝|a|2＝1，b2＝|b|2＝1，
∴a2＝b2，故选D．
3．在△ABC中，eq \(AB,\s\up6(→))·eq \(CB,\s\up6(→))<0，则△ABC的形状是( )
A．锐角三角形 B．直角三角形
C．钝角三角形 D．不能确定
[答案] C
[解析] ∵eq \(AB,\s\up6(→))与eq \(CB,\s\up6(→))的夹角与角B相等，又eq \(AB,\s\up6(→))·eq \(CB,\s\up6(→))<0，
∴csB<0，又∵0≤B≤π，
∴B为钝角，故选C．
4．若|a|＝4，|b|＝2，a和b的夹角为30°，则a在b方向上的投影为( )
A．2 B．eq \r(3)
C．2eq \r(3) D．4
[答案] C
[解析] a在b方向上的投影为|a|cs＝4×cs30°＝2eq \r(3).
5．|m|＝2，m·n＝8，＝60°，则|n|＝( )
A．5 B．6
C．7 D．8
[答案] D
[解析] ∵eq \f(m·n,|m|·|n|)＝cs，
∴eq \f(8,2|n|)＝eq \f(1,2)，∴|n|＝8.
6．向量a的模为10，它与x轴的夹角为150°，则它在x轴上的投影为( )
A．－5eq \r(3) B．5
C．－5 D．5eq \r(3)
[答案] A
[解析] a在x轴上的投影为|a|·cs150°＝－5eq \r(3).
二、填空题
7．已知a·b＝16，若a与b方向上的射影数量为4，则|b|＝________.
[答案] 4
[解析] 设a与b的夹角为θ，
∵a·b＝16，∴|a||b|csθ＝16.
又∵a在b方向上的射影的数量为4，
∴|a|csθ＝4，∴|b|＝4.
8．若等腰△ABC的底边BC长为4，则eq \(BA,\s\up6(→))·eq \(BC,\s\up6(→))＝________.
[答案] 8
[解析] 如图，
取BC的中点D，连接AD，∵AB＝AC，
∵AD⊥BC．∴ABcsB＝BD＝2.
∴eq \(BA,\s\up6(→))·eq \(BC,\s\up6(→))＝|eq \(BA,\s\up6(→))|·|eq \(BC,\s\up6(→))|csB
＝2×4＝8.
三、解答题
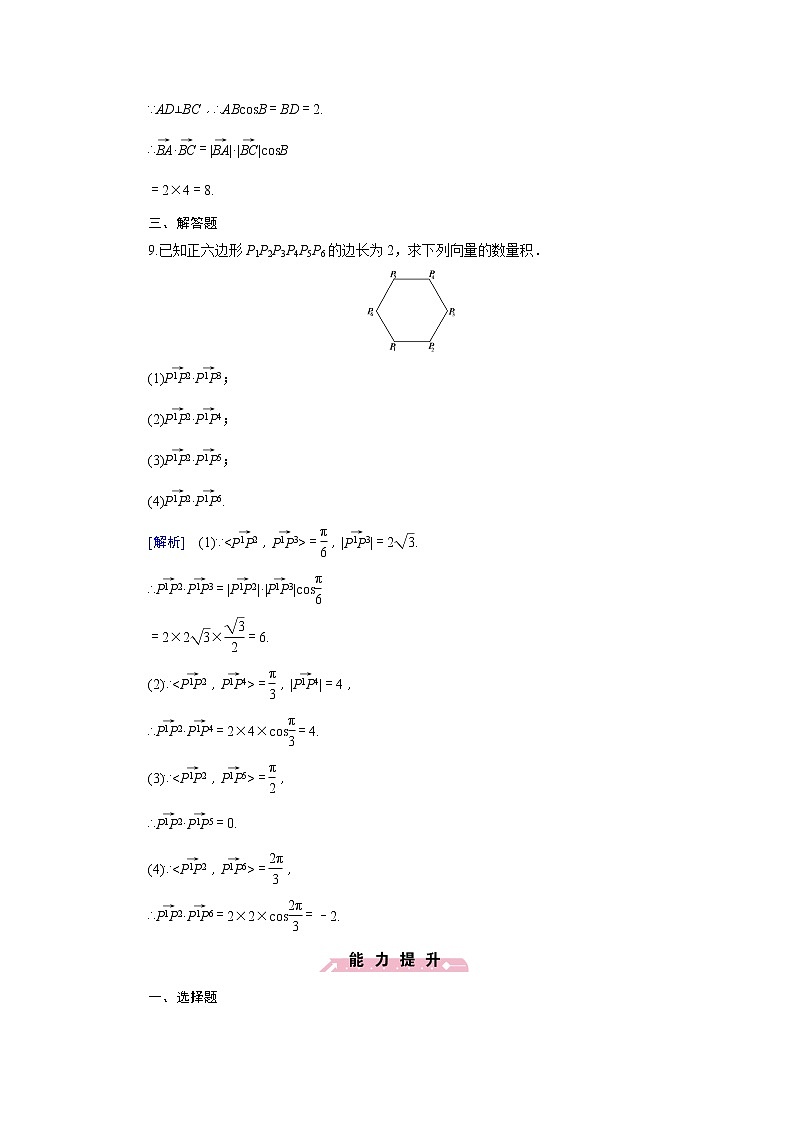
9.已知正六边形P1P2P3P4P5P6的边长为2，求下列向量的数量积．
(1)eq \(P1P2,\s\up6(→))·eq \(P1P3,\s\up6(→))；
(2)eq \(P1P2,\s\up6(→))·eq \(P1P4,\s\up6(→))；
(3)eq \(P1P2,\s\up6(→))·eq \(P1P5,\s\up6(→))；
(4)eq \(P1P2,\s\up6(→))·eq \(P1P6,\s\up6(→)).
[解析] (1)∵＝eq \f(π,6)，|eq \(P1P3,\s\up6(→))|＝2eq \r(3).
∴eq \(P1P2,\s\up6(→))·eq \(P1P3,\s\up6(→))＝|eq \(P1P2,\s\up6(→))|·|eq \(P1P3,\s\up6(→))|cseq \f(π,6)
＝2×2eq \r(3)×eq \f(\r(3),2)＝6.
(2)∵＝eq \f(π,3)，|eq \(P1P4,\s\up6(→))|＝4，
∴eq \(P1P2,\s\up6(→))·eq \(P1P4,\s\up6(→))＝2×4×cseq \f(π,3)＝4.
(3)∵＝eq \f(π,2)，
∴eq \(P1P2,\s\up6(→))·eq \(P1P5,\s\up6(→))＝0.
(4)∵＝eq \f(2π,3)，
∴eq \(P1P2,\s\up6(→))·eq \(P1P6,\s\up6(→))＝2×2×cseq \f(2π,3)＝－2.
一、选择题
1．对于向量a、b、c和实数λ，下列命题中真命题是( )
A．若a·b＝0，则a＝0或b＝0
B．若λa＝0，则λ＝0或a＝0
C．若a2＝b2，则a＝b或a＝－b
D．若a·b＝a·c，则b＝c
[答案] B
[解析] A中，若a·b＝0，则a＝0或b＝0或a⊥b，故A错；C中，若a2＝b2，则|a|＝|b|，C错；D中，若a·b＝a·c，则可能有a⊥b，a⊥c，但b≠c，故只有选项B正确．
2．已知向量a、b满足|a|＝1，|b|＝4，且a·b＝2，则a与b的夹角为( )
A．eq \f(π,6) B．eq \f(π,4)
C．eq \f(π,3) D．eq \f(π,2)
[答案] C
[解析] cs＝eq \f(a·b,|a|·|b|)＝eq \f(2,4)＝eq \f(1,2)，
又∵∈[0，π]，∴＝eq \f(π,3).
3．有下列四个式子：
①0·a＝0；
②0·a＝0；
③0－eq \(MN,\s\up6(→))＝eq \(NM,\s\up6(→))；
④|a·b|＝|a||b|，
其中正确的个数为( )
A．4个 B．3个
C．2个 D．1个
[答案] D
[解析] 0·a＝0，故①错；0·a＝0，故②错；0－eq \(MN,\s\up6(→))＝eq \(NM,\s\up6(→))，故③正确；|a·b|＝|a||b|cs〈a，b〉，故④错，
∴选D．
4．已知平面上三点A、B、C，满足|eq \(AB,\s\up6(→))|＝3，|eq \(BC,\s\up6(→))|＝4，|eq \(CA,\s\up6(→))|＝5，则eq \(AB,\s\up6(→))·eq \(BC,\s\up6(→))＋eq \(BC,\s\up6(→))·eq \(CA,\s\up6(→))＋eq \(CA,\s\up6(→))·eq \(AB,\s\up6(→))的值等于( )
A．－7 B．7
C．28 D．－28
[答案] D
[解析] 由题意可知，A、B、C三点不共线，
∴|eq \(CA,\s\up6(→))|2＝|AB|2＋|BC|2，
∴∠B为直角，∴csB＝0，
csA＝eq \f(3,5)，csC＝eq \f(4,5).
∴eq \(AB,\s\up6(→))·eq \(BC,\s\up6(→))＋eq \(BC,\s\up6(→))·eq \(CA,\s\up6(→))＋eq \(CA,\s\up6(→))·eq \(AB,\s\up6(→))
＝|eq \(AB,\s\up6(→))|·|eq \(BC,\s\up6(→))|csB＋|eq \(BC,\s\up6(→))||eq \(CA,\s\up6(→))|cs(π－C)＋
|eq \(CA,\s\up6(→))||eq \(AB,\s\up6(→))|cs(π－A)
＝0＋4×5×(－eq \f(4,5))＋5×4×(－eq \f(3,5))＝－28.
二、填空题
5．已知|a|＝4，|b|＝5，则a在b上的射影的数量与b在a上的射影的数量的比值λ＝________.
[答案] eq \f(4,5)
[解析] a在b上的射影的数量等于|a|cs〈a，b〉，b在a上的射影的数量等于|b|cs〈b，a〉，
∴λ＝eq \f(|a|cs〈a，b〉,|b|cs〈b，a〉)＝eq \f(4,5).
6．对于任意向量a、b，定义新运算“⊗”：a⊗b＝|a|·|b|·sinθ(其中θ为a与b的夹角)．利用这个新知识解决：若|a|＝1，|b|＝5，且a·b＝4，则a⊗b＝________.
[答案] 3
[解析] 设向量a与b的夹角为θ，则csθ＝eq \f(a·b,|a|·|b|)＝eq \f(4,5)，∴sinθ＝eq \f(3,5).
∴a⊗b＝|a|·|b|·sinθ＝1×5×eq \f(3,5)＝3.
三、解答题
7.如图所示，在▱ABCD中，|eq \(AB,\s\up6(→))|＝4，|eq \(AD,\s\up6(→))|＝3，∠DAB＝60°.求：
(1)eq \(AD,\s\up6(→))·eq \(BC,\s\up6(→))；
(2)eq \(AB,\s\up6(→))·eq \(CD,\s\up6(→))；
(3)eq \(AB,\s\up6(→))·eq \(DA,\s\up6(→)).
[解析] (1)因为eq \(AD,\s\up6(→))∥eq \(BC,\s\up6(→))，且方向相同，所以eq \(AD,\s\up6(→))与eq \(BC,\s\up6(→))夹角是0°.所以eq \(AD,\s\up6(→))·eq \(BC,\s\up6(→))＝|eq \(AD,\s\up6(→))|·|eq \(BC,\s\up6(→))|·cs0°＝3×3×1＝9.
(2)因为eq \(AB,\s\up6(→))∥eq \(CD,\s\up6(→))，且方向相反，所以eq \(AB,\s\up6(→))与eq \(CD,\s\up6(→))的夹角是180°，所以eq \(AB,\s\up6(→))·eq \(CD,\s\up6(→))＝|eq \(AB,\s\up6(→))|·|eq \(CD,\s\up6(→))|·cs180°＝4×4×(－1)＝－16.
(3)eq \(AB,\s\up6(→))与eq \(AD,\s\up6(→))的夹角为60°，
所以eq \(AB,\s\up6(→))与eq \(DA,\s\up6(→))的夹角为120°，(←此处易错为60°.)
所以eq \(AB,\s\up6(→))·eq \(DA,\s\up6(→))＝|eq \(AB,\s\up6(→))|·|eq \(DA,\s\up6(→))|·cs120°＝4×3×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))＝－6.
8.已知|a|＝2|b|≠0，且关于x的方程x2＋|a|x＋a·b＝0有实根，求a与b的夹角的取值范围．
[解析] ∵方程x2＋|a|x＋a·b＝0有实根，
∴Δ＝|a|2－4a·b≥0，
∴a·b≤eq \f(1,4)|a|2.
cs＝eq \f(a·b,|a|·|b|)＝eq \f(a·b,|a|·\f(|a|,2))＝eq \f(a·b,\f(1,2)|a|2)≤eq \f(\f(1,4)|a|2,\f(1,2)|a|2)＝eq \f(1,2)，
又∵0≤≤π，∴eq \f(π,3)≤≤π.
即a与b的夹角的取值范围为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，π)).

相关试卷更多