初中数学沪科版九年级下册24.3.2 圆内接四边形优秀备课ppt课件

这是一份初中数学沪科版九年级下册24.3.2 圆内接四边形优秀备课ppt课件，共23页。PPT课件主要包含了课堂小结等内容，欢迎下载使用。
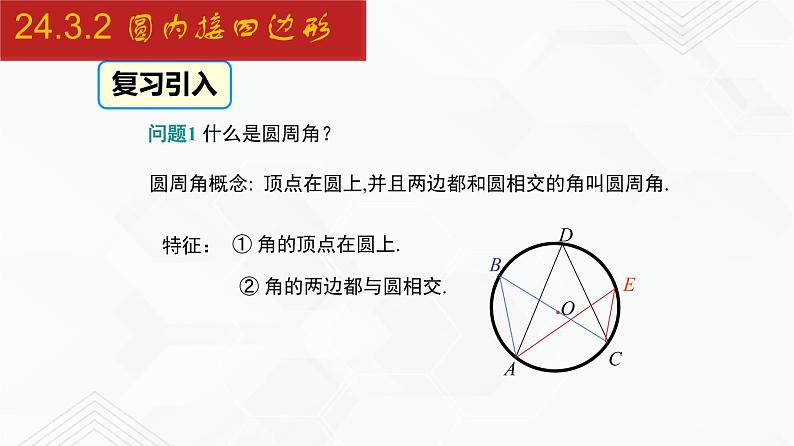
问题1 什么是圆周角？
② 角的两边都与圆相交.
圆周角概念: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
24.3.2 圆内接四边形
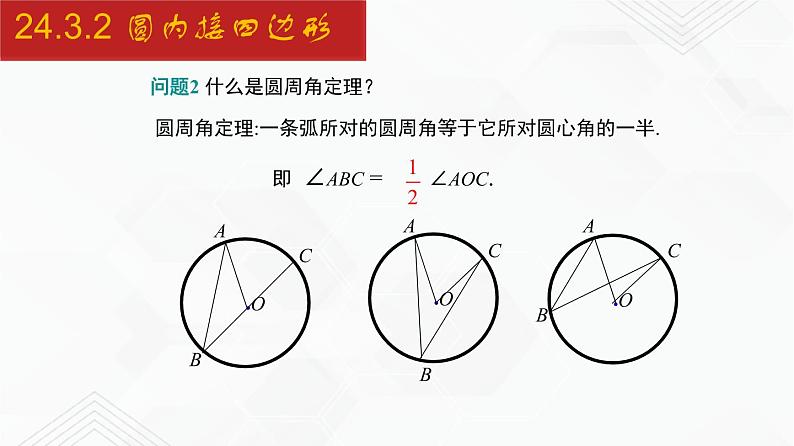
问题2 什么是圆周角定理？
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
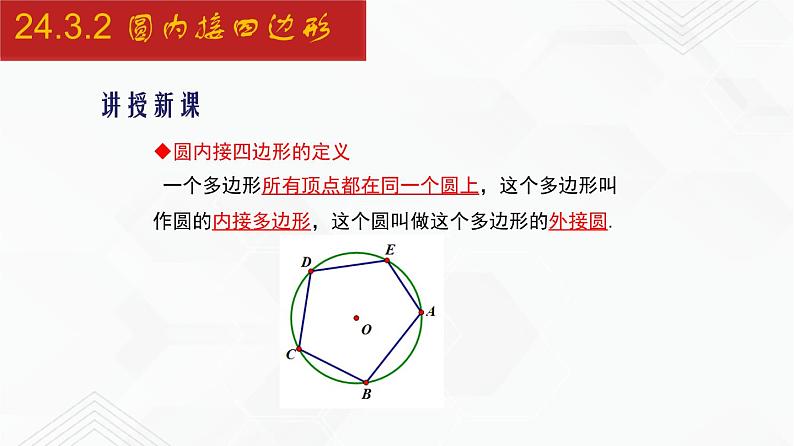
一个多边形所有顶点都在同一个圆上，这个多边形叫作圆的内接多边形，这个圆叫做这个多边形的外接圆.
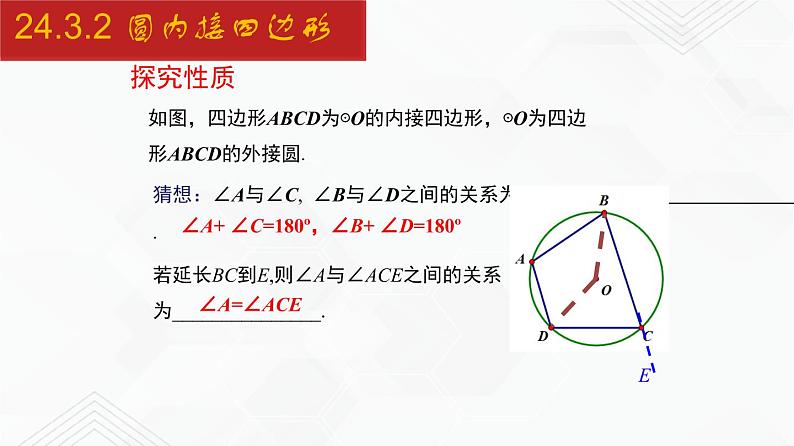
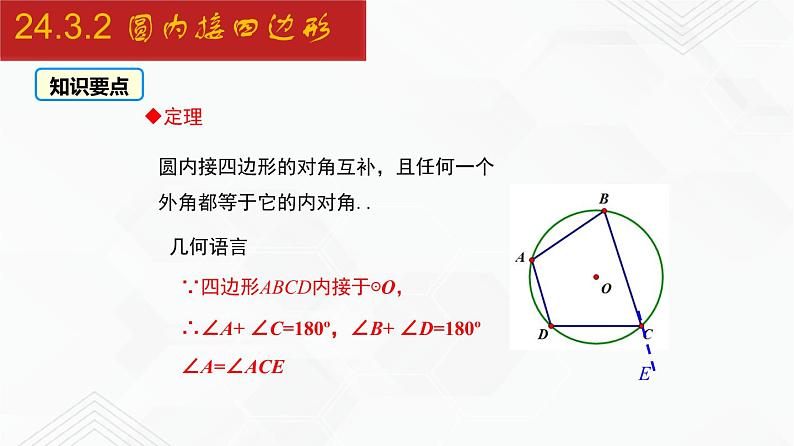
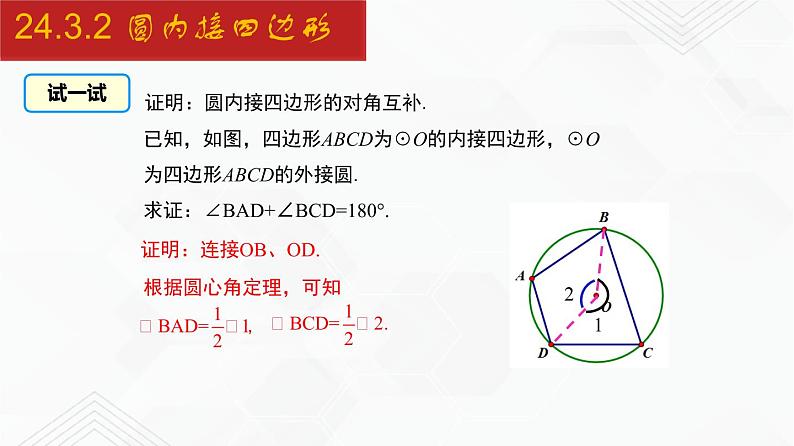
如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关系为 .
∠A+ ∠C=180º，∠B+ ∠D=180º
若延长BC到E,则∠A与∠ACE之间的关系为_______________.
圆内接四边形的对角互补，且任何一个外角都等于它的内对角..
∴∠A+ ∠C=180º，∠B+ ∠D=180º
∵四边形ABCD内接于⊙O，
证明：圆内接四边形的对角互补.
已知，如图，四边形ABCD为☉O的内接四边形，☉O为四边形ABCD的外接圆. 求证：∠BAD+∠BCD=180°.
证明：连接OB、OD.
解：设∠A，∠B，∠C的度数分别对于2x，3x，6x，
例1 在圆内接四边形ABCD中， ∠A，∠B，∠C的度数之比是2︰3︰6.求这个四边形各角的度数.
∵四边形ABCD内接于圆，
∴ ∠A+ ∠C=∠B+∠D=180°，
∵2x+6x=180°，
∴ ∠A=45°， ∠B=67.5°， ∠C =135°， ∠D=180°-67.5°=112.5°.
例2、如图⊙O1与⊙O2都经过A、B两点，经过点A的直线CD与⊙O1 交于点C，与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E，与⊙O2 交于点F。求证：CE∥DF
∠E＋∠1＝180°、∠1＝∠F
证明两条直线平行的方法很多，但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF，想一想还能否通过同位角相等或者内错角相等证明结果？
1）延长EF,是否有∠E=∠BAD＝ ∠1 ?
延长DF,　能否证明∠E＝∠２＝∠3？
例3、求证：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．（提示：作出以这条边为直径的圆.）
求证： △ABC 为直角三角形.
已知：△ABC 中，CO为AB边上的中线，CO= 1/2AB
∴ △ABC 为直角三角形.
例4、已知：如图，四边形ABCD是圆的内接四边形并且ABCD是平行四边形。
求证：四边形ABCD是矩形。
ABCD是平行四边形∠A+ ∠D=1800 ，∠C+ ∠D=1800 ，∠A= ∠C
四边形ABCD是圆的内接四边形∠A+ ∠C=1800 ∠A= ∠C=900
例4、 如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．
又在Rt△ABD中，AD2+BD2=AB2，
∴ ∠ACB= ∠ADB=90°．
1．四边形ABCD是☉O的内接四边形，且∠A=110°，∠B=80°，则∠C= ，∠D= .2．☉O的内接四边形ABCD中，∠A∶∠B∶∠C=1∶2∶3 ，则∠D= .
1.若ABCD为圆内接四边形，则下列哪个选项可能成立（ ）
A.∠A∶∠B∶∠C∶∠D ＝ 1∶2∶3∶4
B.∠A∶∠B∶∠C∶∠D ＝ 2∶1∶3∶4
C.∠A∶∠B∶∠C∶∠D ＝ 3∶2∶1∶4
D.∠A∶∠B∶∠C∶∠D ＝ 4∶3∶2∶1
4.在⊙O中，∠CBD=30°，∠BDC=20°,求∠A.
解：∵∠CBD=30°，∠BDC=20°∴∠C=180°-∠CBD-∠BDC=130°∴∠A=180°-∠C=50°（圆内接四边形对角互补）
5.如图，已知A，B，C，D是⊙O上的四点，延长DC，AB相交于点E.若BC＝BE.求证：△ADE是等腰三角形．
证明：∵A，D，C，B四点共圆，∴∠A=∠BCE，∵BC=BE，∴∠BCE=∠E，∴∠A=∠E，∴AD=DE，即△ADE是等腰三角形．
6.如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E，F．（1）若∠E+∠F=α，求∠A的度数（用含α的式子表示）；（2）若∠E+∠F=60°，求∠A的度数．
（2）当α=60°时，
解：（1）∵四边形ABCD为⊙O的内接四边形，
∵∠EBF=∠A+∠E，
而∠EBF=180°－∠BCF－∠F，
∴∠A+∠E=180°－∠BCF－∠F，
∴∠A+∠E=180°－∠A－∠F，
即2∠A=180°－(∠E+∠F)，
一个多边形所有顶点都在同一个圆上，这个多边形叫作圆的内接多边形，这个圆叫做这个多边形的外接圆.