高中数学人教B版 (2019)必修 第四册第十章 复数10.1 复数及其几何意义10.1.1 复数的概念一等奖课件ppt

这是一份高中数学人教B版 (2019)必修 第四册第十章 复数10.1 复数及其几何意义10.1.1 复数的概念一等奖课件ppt，共18页。PPT课件主要包含了情景与问题，b≠0，纯虚数，非纯虚数，a≠0且b≠0，自然数，有理数，无理数，数系的扩充，x-2等内容，欢迎下载使用。
数的扩充过程，也可以从方程是否有解的角度来理解： 因为类似x+4=3的方程在自然数范围内无解，所以人们引入了负数并将自然数扩充成整数，使得类似x+ 4=3的方程在整数范围内有解； 因为类似2x=5的方程在整数范围内无解,所以人们引入了分数并将整数扩充成有理数，使得类似2x=5的方程在有理数范围内有解； 因为类似x2=7的方程在有理数范围内无解,所以人们引入了无理数并将有理数扩充成实数,使得类似x2=7的方程在实数范围内有解. 我们已经知道，类似x2=-1的方程在实数范围内无解.那么，能否像前面一 样,引入一种新的数，使得这个方程有解并将实数进行扩充呢？
人们早在16世纪就发现，可以通过公式来求方程x3=px+q(p,q均为正实数)的正根。
例如，方程x3=9x+28的正根为
如果方程是x3=15x+4，则由公式可得
当时人们已经知道x=4是x3=9x+28的唯一正根，因此应该成立。
所以可以认为
一般地，为了使得方程x2=一1有解,人们规定 i 的平方等于一 1.即 i2=-1并称 i为虚数单位.
（1）你认为可以怎样表示2与 i 的和？又该怎样表示3减去i ?（2）你认为5与 i 的乘积可以怎样表示？这个数具有什么性质？
实数 a 与 i 的和记作 a+i .
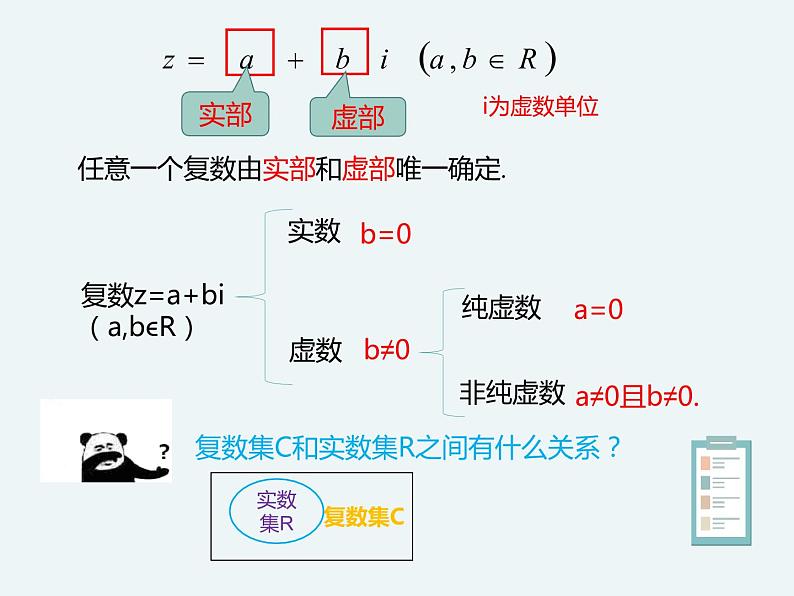
复数：形如a+bi的数（a,b 是实数），复数一般用小写字母z表示. 即z= a + b i (a,bϵR).其中a称为z的实部，b称为z的虚部， 分别记作 Re(z)=a, Im(z)=b.
复数全体组成的集合叫复数集，记作：C
C={ z| z=a+bi ,a,bϵR }
实数 0 与 i 的和为 i ;
实数 b 与 i 的积记作 bi
实数 0 与 i 的积为 0 ,
实数 1 与 i 的积为 i .
任意一个复数由实部和虚部唯一确定.
复数集C和实数集R之间有什么关系？
复数z=a+bi（a,bϵR）
根据实际需要把数进行扩充。
分别求实数x的取值，使得复数z = (x — 2) + (x+ 3)i (1)是实数；(2)是虚数；(3)是纯虚数.
分析：复数z的实部是
复数 z的虚部是
(1)当 x+3=0，即 x=-3 时，复数z是实数.
(2)当 x+3 ≠ 0，即 x≠ -3 时，复数z是虚数.
(3)当 x-2=0 且 x+3≠0，即 x=2 时，复数z是存虚数.
练习A3.分别写出下列各复数的实部与虚部.(1) -3+2i；(2) 3-5i；(3) -7；(4) 8i.
练习B2.分别求实数m的取值范围，使得复数E=(m+2)+(m-6)i (1)是实数； (2)是虚数； (3)是纯虚数・
解： (1) m = 6； (2)m≠6 (3) m = -2,
1 当实数m为何值时， 分别是： （1）实数；（2）虚数；（3）纯虚数
【解】由已知得复数z的实部为
虚部为 m2+5m+6.
2.如果（m2-1）+（m2-2m）i>0，则实数m的值为　　　　.
解：m2-1>0 且 m2-2m=0 所以m=2.
分析：两个实数可以比较大小，但是当两个复数中至少有一个是虚数时，则不可以比较大小.如果两个复数可以比较大小，那么这两个复数必定全是实数.
复数相等：两个复数z1与z2，实部与虚部对应相等，就称这两个复数相等， 记作：z1=z2
如果a,b,c,d都是实数，那么
【注意】两个不相等的实数，可以比较大小; 但是两个复数，如果不全是实数，一般不规定它们之间的大小，只能说它们相等或不相等.
分别求满足下列关系的实数x与y的值.(1) (x+2y )—i=6x + (x一y) i ;(2) (x + y+ 1) —(x—y + 2) i =0 .
（1）根据复数相等的定义，得
（2）由复数等于0的充要条件，得
两复数相等等价于其实部与虚部分别对应相等。
复数为0是实部为0，虚部也为0.
练习A 4.已知(x-2)+ yi=0,求实数x与y的值.
4解. x=2, y=0.
练习B 3.分别求满足下列关系的实数x与y的值. (1) (x+y-3)+ (x-y-1)i = 3 + 3i； (2) (x+y + 1)—(x—2y + l)i=0,
练习A 5.已知z1的实部是1, z2的实部为0,则z1=z2可能成立吗？ 为什么？
解：5. 不可能.因为两个复数z1与z2，只有实部与虚部都对应相等才能说它们相等.
练习B 4.写出复数是正实数的一个充要条件
解：4. 复数是正实数的一个充要条件是：复数的实部为正实数且虚部等于零.
1.已知关于实数x，y的方程组
有实数解，求实数a，b的值.
解：根据复数相等的充要条件，得
代入②，得5+4a-（6+b）i＝9-8i 且a，b∈R
【注意】如果两个复数不全是实数，一般不规定它们之间的大小，只能说它们相等或不相等.