2019版高考数学（理）一轮精选教师用书人教通用：第4章7第7讲　正弦定理与余弦定理

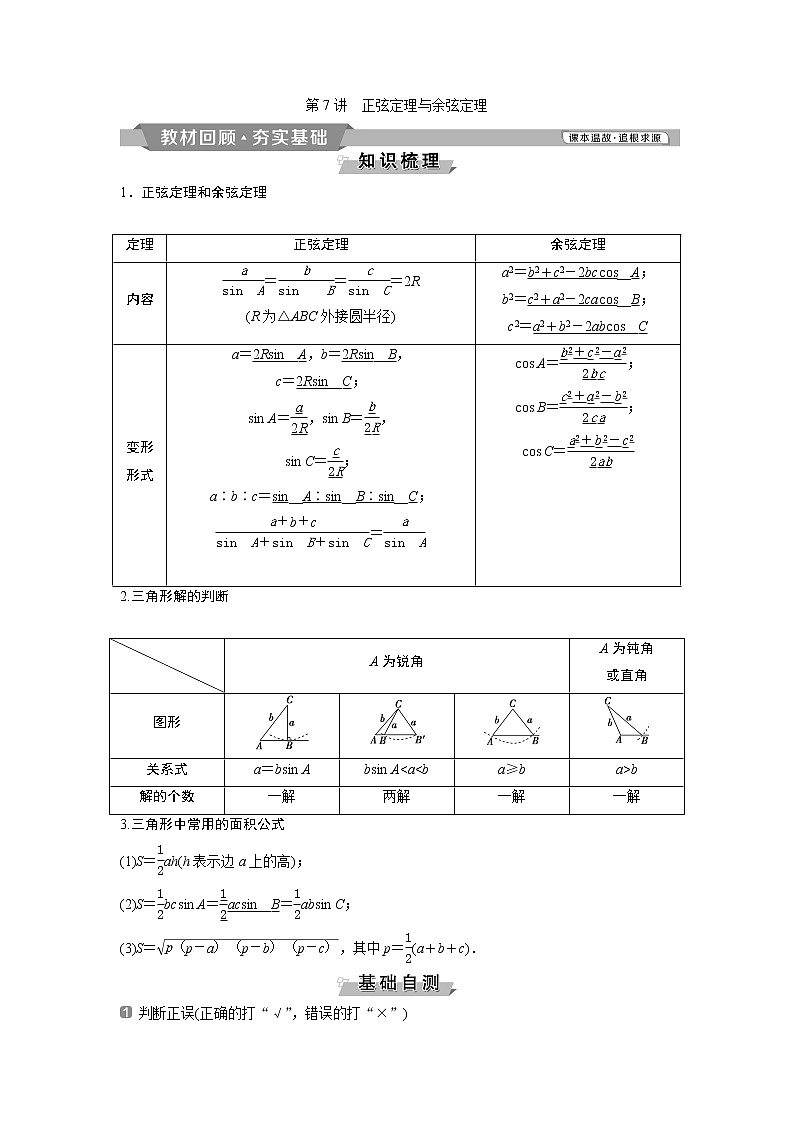
第7讲　正弦定理与余弦定理

1．正弦定理和余弦定理

定理
正弦定理
余弦定理
内容
＝＝＝2R
(R为△ABC外接圆半径)
a2＝b2＋c2－2bccos__A；
b2＝c2＋a2－2cacos__B；
c2＝a2＋b2－2abcos__C
变形形式
a＝2Rsin__A，b＝2Rsin__B，
c＝2Rsin__C；
sin A＝，sin B＝，
sin C＝；
a∶b∶c＝sin__A∶sin__B∶sin__C；
＝
cos A＝；
cos B＝；
cos C＝
2.三角形解的判断


A为锐角
A为钝角
或直角
图形




关系式
a＝bsin A
bsin A a≥b
a>b
解的个数
一解
两解
一解
一解
3.三角形中常用的面积公式
(1)S＝ah(h表示边a上的高)；
(2)S＝bcsin A＝acsin__B＝absin C；
(3)S＝，其中p＝(a＋b＋c)．

判断正误(正确的打“√”，错误的打“×”)
(1)在△ABC中，已知a，b和角B，能用正弦定理求角A；已知a，b和角C，能用余弦定理求边c.(　　)
(2)在三角形中，已知两角和一边或已知两边和一角都能解三角形．(　　)
(3)在△ABC中，sin A>sin B的充分不必要条件是A>B.(　　)
(4)在△ABC中，a2＋b2 (5)在△ABC的角A，B，C，边长a，b，c中，已知任意三个可求其他三个．(　　)
答案：(1)√　(2)√　(3)×　(4)√　(5)×
(教材习题改编)在△ABC中，已知a＝5，b＝7，c＝8，则A＋C＝(　　)
A．90°　　 B．120°
C．135° D．150°
解析：选B.cos B＝＝＝.
所以B＝60°，所以A＋C＝120°.
在△ABC中，若a＝18，b＝24，A＝45°，则此三角形(　　)
A．无解 B．有两解
C．有一解 D．解的个数不确定
解析：选B.因为＝，
所以sin B＝·sin A＝×sin 45°＝.
又因为a 在△ABC中，角A，B，C所对的边分别为a，b，c，cos 2A＝sin A，bc＝2，则△ABC的面积为________．
解析：由cos 2A＝sin A，得1－2sin2A＝sin A，解得sin A＝(负值舍去)，由bc＝2，可得△ABC的面积S＝bcsin A＝×2×＝.
答案：
(2017·高考全国卷Ⅱ)△ABC的内角A，B，C的对边分别为a，b，c，若2bcos B＝acos C＋ccos A，则B＝________．
解析：依题意得2b×＝a×＋c×，即a2＋c2－b2＝ac，所以2accos B＝ac>0，cos B＝.又0 答案：


　　　　　　利用正弦、余弦定理解三角形
[典例引领]
(1)(2016·高考全国卷Ⅲ)在△ABC中，B＝，BC边上的高等于BC，则cos A＝(　　)
A.　　　　　　　　　 B.
C．－ D．－
(2)(2017·高考全国卷Ⅰ)△ABC的内角A、B、C的对边分别为a、b、c.已知sin B＋sin A(sin C－cos C)＝0，a＝2，c＝，则C＝(　　)
A. B.
C. D.
【解析】　(1)设△ABC中角A，B，C的对边分别是a，b，c，由题意可得a＝csin ＝c，则a＝c.在△ABC中，由余弦定理可得b2＝a2＋c2－ac＝c2＋c2－3c2＝c2，则b＝c.由余弦定理，可得cos A＝＝＝－，故选C.
(2)因为sin B＋sin A(sin C－cos C)＝0，所以sin(A＋C)＋sin A·sin C－sin A·cos C＝0，所以sin Acos C＋cos Asin C＋sin Asin C－sin Acos C＝0，整理得sin C(sin A＋cos A)＝0，因为sin C≠0，所以sin A＋cos A＝0，所以tan A＝－1，因为A∈(0，π)，所以A＝，由正弦定理得sin C＝＝＝，又0 【答案】　(1)C　(2)B

(1)正、余弦定理的选用
解三角形时，如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到．
(2)三角形解的个数的判断
已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断．　
[通关练习]
1．(2018·张掖市第一次诊断考试)在△ABC中，内角A，B，C的对边分别是a，b，c，若c＝2a，bsin B－asin A＝asin C，则cos B为(　　)
A. B.
C. D.
解析：选B.由bsin B－asin A＝asin C，且c＝2a，得b＝a，所以cos B＝＝＝.
2．已知△ABC中，a，b，c分别是角A，B，C所对的边，若(2a＋c)cos B＋bcos C＝0，则角B的大小为(　　)
A. B.
C. D.
解析：选C.法一：因为(2a＋c)cos B＋bcos C＝0，所以(2sin A＋sin C)cos B＋sin Bcos C＝2sin Acos B＋sin(B＋C)＝2sin Acos B＋sin A＝0，
因为sin A≠0，所以cos B＝－，又B为△ABC的内角，所以B＝.故选C.
法二：因为(2a＋c)cos B＋bcos C＝0，
所以(2a＋c)·＋b·＝0，
所以b2＝a2＋c2＋ac，
所以cos B＝＝－，
所以B＝.
3．在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若a＝3，∠B＝2∠A，cos A＝，则b＝________．
解析：在△ABC中，由cos A＝，∠B＝2∠A，可得sin A＝，
sin B＝sin 2A＝2sin Acos A＝2××＝.
再由正弦定理＝，可得＝，
求得b＝2.
答案：2

　　　　　　利用正弦、余弦定理判定三角形
的形状
[典例引领]
(1)设△ABC的内角A，B，C所对的边分别为a，b，c，若bcos C＋ccos B＝asin A，则△ABC的形状为(　　)
A．直角三角形 B．锐角三角形
C．钝角三角形 D．不确定
(2)(2018·山西怀仁月考)若a2＋b2－c2＝ab，且2cos Asin B＝sin C，那么△ABC一定是(　　)
A．直角三角形 B．等腰三角形
C．等腰直角三角形 D．等边三角形
【解析】　(1)由正弦定理得sin Bcos C＋cos Bsin C＝sin2A，则sin(B＋C)＝sin2A，由三角形内角和，得sin(B＋C)＝sin A＝sin2A，即sin A＝1，所以∠A＝.即△ABC为直角三角形．
(2)法一：利用边的关系来判断：
由正弦定理得＝，由2cos Asin B＝sin C，有cos A＝＝.
又由余弦定理得cos A＝，
所以＝，
即c2＝b2＋c2－a2，所以a2＝b2，
所以a＝b.又因为a2＋b2－c2＝ab.
所以2b2－c2＝b2，所以b2＝c2，
所以b＝c，所以a＝b＝c.
所以△ABC为等边三角形．
法二：利用角的关系来判断：
因为A＋B＋C＝180°，所以sin C＝sin(A＋B)，
又因为2cos Asin B＝sin C，
所以2cos Asin B＝sin Acos B＋cos Asin B，
所以sin(A－B)＝0.
又因为A与B均为△ABC的内角，所以A＝B，
又由a2＋b2－c2＝ab，
由余弦定理，得cos C＝＝＝，又0° 所以△ABC为等边三角形．
【答案】　(1)A　(2)D

若将本例(1)条件改为“2sin Acos B＝sin C”，试判断△ABC的形状．
解：法一：由已知得2sin Acos B＝sin C＝sin(A＋B)＝sin Acos B＋cos Asin B，即sin(A－B)＝0，因为－π＜A－B＜π，所以A＝B，故△ABC为等腰三角形．
法二：由正弦定理得2acos B＝c，再由余弦定理得
2a·＝c⇒a2＝b2⇒a＝b，
故△ABC为等腰三角形．

判定三角形形状的两种常用途径

[提醒]　“角化边”后要注意用因式分解、配方等方法得出边的相应关系；“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系．　
[通关练习]
1．在△ABC中，角A，B，C所对的边分别为a，b，c，若＜cos A，则△ABC为(　　)
A．钝角三角形 B．直角三角形
C．锐角三角形 D．等边三角形
解析：选A.已知＜cos A，由正弦定理，得＜cos A，即sin C＜sin Bcos A，所以sin(A＋B)＜sin Bcos A，即sin B·cos A＋cos Bsin A－sin Bcos A＜0，所以cos Bsin A＜0.又sin A＞0，于是有cos B＜0，B为钝角，所以△ABC是钝角三角形．
2．在△ABC中，a，b，c分别为内角A，B，C的对边，且2asin A＝(2b＋c)sin B＋(2c＋b)sin C.
(1)求角A的大小；
(2)若sin B＋sin C＝1，试判断△ABC的形状．
解：(1)由题意知，
根据正弦定理得2a2＝(2b＋c)b＋(2c＋b)c，
即a2＝b2＋c2＋bc.①
由余弦定理得a2＝b2＋c2－2bccos A，
故cos A＝－，
A＝120°.
(2)由①得sin2A＝sin2B＋sin2C＋sin Bsin C.
又sin B＋sin C＝1，故sin B＝sin C＝.
因为0° 所以△ABC是等腰钝角三角形．

　　　　　　与三角形面积有关的问题(高频考点)
求解与三角形面积有关的问题是高考的热点，三种题型在高考中时有出现，其试题为中档题．高考对正、余弦定理应用的考查有以下三个命题角度：
(1)求三角形的面积；
(2)已知三角形的面积解三角形；
(3)求有关三角形面积或周长的最值(范围)问题．
[典例引领]
角度一　求三角形的面积
(2017·高考全国卷Ⅲ)△ABC的内角A，B，C的对边分别为a，b，c，已知sin A＋cos A＝0，a＝2，b＝2.
(1)求c；
(2)设D为BC边上一点，且AD⊥AC，求△ABD的面积．
【解】　(1)由已知可得tan A＝－，所以A＝.
在△ABC中，由余弦定理得28＝4＋c2－4ccos，即c2＋2c－24＝0.
解得c＝－6(舍去)，c＝4.
(2)由题设可得∠CAD＝，所以∠BAD＝∠BAC－∠CAD＝.
故△ABD面积与△ACD面积的比值为
＝1.
又△ABC的面积为×4×2sin∠BAC＝2，所以△ABD的面积为.
角度二　已知三角形的面积解三角形
(2018·江西南昌十校模拟)在△ABC中，a，b，c分别是内角A，B，C的对边，且B为锐角，若＝，sin B＝，S△ABC＝，则b的值为________．
【解析】　由＝⇒＝⇒a＝c，①
由S△ABC＝acsin B＝且sin B＝得ac＝5，②
联立①②解得a＝5，c＝2，由sin B＝且B为锐角知cos B＝，由余弦定理知b2＝25＋4－2×5×2×＝14，b＝.
【答案】　
角度三　求有关三角形面积或周长的最值(范围)
问题
(2018·沈阳市教学质量检测(一))已知△ABC的三个内角A，B，C的对边分别为a，b，c，面积为S，且满足4S＝a2－(b－c)2，b＋c＝8，则S的最大值为________．
【解析】　由题意得：4×bcsin A＝a2－b2－c2＋2bc，
又a2＝b2＋c2－2bccos A，代入上式得：2bcsin A＝－2bccos A＋2bc，即sin A＋cos A＝1，sin＝1，又0 【答案】　8

与三角形面积有关问题的解题策略
(1)求三角形的面积．对于面积公式S＝absin C＝acsin B＝bcsin A，一般是已知哪一个角就使用含哪个角的公式．
(2)已知三角形的面积解三角形．与面积有关的问题，一般要利用正弦定理或余弦定理进行边和角的互化．
(3)求有关三角形面积或周长的最值(范围)问题．一般转化为一个角的一个三角函数，利用三角函数的有界性求解，或利用余弦定理转化为边的关系，再应用基本不等式求解．　
[通关练习]
1．(2018·云南省第一次统一检测)已知△ABC的内角A，B，C的对边分别为a，b，c.若a＝bcos C＋csin B，且△ABC的面积为1＋，则b的最小值为(　　)
A．2　　　　 B．3
C. D.
解析：选A.由a＝bcos C＋csin B及正弦定理，得sin A＝sin Bcos C＋sin Csin B，即sin(B＋C)＝sin Bcos C＋sin Csin B，得sin Ccos B＝sin Csin B，又sin C≠0，所以tan B＝1.
因为B∈(0，π)，所以B＝.由S△ABC＝acsin B＝1＋，得ac＝2＋4.又b2＝a2＋c2－2accos B≥2ac－ac＝(2－)(4＋2)＝4，当且仅当a＝c时等号成立，所以b≥2，b的最小值为2，故选A.
2．(2017·高考全国卷Ⅱ)△ABC的内角A，B，C的对边分别为a，b，c，已知sin(A＋C)＝8sin2.
(1)求cos B；
(2)若a＋c＝6，△ABC的面积为2，求b.
解：(1)由题设及A＋B＋C＝π得sin B＝8sin2，故
sin B＝4(1－cos B)．
上式两边平方，整理得
17cos2B－32cos B＋15＝0，
解得cos B＝1(舍去)，cos B＝.
(2)由cos B＝得sin B＝，故S△ABC＝acsin B＝ac.又S△ABC＝2，则ac＝.
由余弦定理及a＋c＝6得
b2＝a2＋c2－2accos B
＝(a＋c)2－2ac(1＋cos B)
＝36－2××
＝4.
所以b＝2.

应用正、余弦定理的解题技巧

技巧
解读
适合题型
典例指引
边化角
将表达式中的边利用公式a＝2Rsin A，b＝2Rsin B，c＝2Rsin C化为角的关系
等式两边是边的齐次形式
例2(1)
角化边
将表达式中的角利用公式转化为边，出现角的正弦值用正弦定理转化，出现角的余弦值由余弦定理转化
等式两边是角的齐次形式、a2＋b2－c2＝λab形式
例2(2)
和积互化
a2＝b2＋c2－2bccos A＝(b＋c)2－2bc(1＋cos A)．可联系已知条件，利用方程思想进行求解三角形的边
出现b＋c，bc等结构形式






方积互化
与重要不等式相联系，由b2＋c2≥2bc，得a2＝b2＋c2－2bccos A≥2bc－2bccos A＝2bc(1－cos A)，可探求边或角的范围问题
求边、角、面积等范围问题　
例3­3
易错防范
(1)在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解或无解，所以要注意分类讨论．
(2)在判断三角形形状时，等式两边一般不要约去公因式，应移项提取公因式，以免漏解．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

1．(2018·兰州市实战考试)△ABC的内角A、B、C的对边分别为a、b、c，若b2＝ac，c＝2a，则cos C＝(　　)
A.　　 B．－
C. D．－
解析：选B.由题意得，b2＝ac＝2a2，b＝a，所以cos C＝＝＝－，故选B.
2．(2018·广东广雅中学、江西南昌二中联考)已知a，b，c为△ABC的三个内角A，B，C所对的边，若3bcos C＝c(1－3cos B)，则sin C∶sin A＝(　　)
A．2∶3 B．4∶3
C．3∶1 D．3∶2
解析：选C.由正弦定理得3sin Bcos C＝sin C－3sin Ccos B，3sin(B＋C)＝sin C，因为A＋B＋C＝π，所以B＋C＝π－A，所以3sin A＝sin C，所以sin C∶sin A＝3∶1，选C.
3．在锐角△ABC中，角A，B，C所对的边分别为a，b，c，若sin A＝，a＝3，S△ABC＝2，则b的值为(　　)
A．6 B．3
C．2 D．2或3
解析：选D.因为S△ABC＝2＝bcsin A，
所以bc＝6，又因为sin A＝，所以cos A＝，又a＝3，由余弦定理得9＝b2＋c2－2bccos A＝b2＋c2－4，b2＋c2＝13，可得b＝2或b＝3.
4．(2018·安徽合肥模拟)△ABC的内角A，B，C的对边分别为a，b，c，若cos C＝，bcos A＋acos B＝2，则△ABC的外接圆面积为(　　)
A．4π B．8π
C．9π D．36π
解析：选C.已知bcos A＋acos B＝2，由正弦定理可得2Rsin Bcos A＋2Rsin Acos B＝2(R为△ABC的外接圆半径)．利用两角和的正弦公式得2Rsin(A＋B)＝2，则2Rsin C＝2，因为cos C＝，所以sin C＝，所以R＝3.故△ABC的外接圆面积为9π.故选C.
5．在△ABC中，内角A，B，C所对应的边分别为a，b，c，若bsin A－acos B＝0，且b2＝ac，则的值为(　　)
A. B.
C．2 D．4
解析：选C.在△ABC中，由bsin A－acos B＝0，
利用正弦定理得sin Bsin A－sin Acos B＝0，
所以tan B＝，故B＝.
由余弦定理得b2＝a2＋c2－2ac·cos B＝a2＋c2－ac，
即b2＝(a＋c)2－3ac，
又b2＝ac，所以4b2＝(a＋c)2，求得＝2.
6．在△ABC中，A＝，b2sin C＝4sin B，则△ABC的面积为________．
解析：因为b2sin C＝4sin B，
所以b2c＝4b，所以bc＝4，
S△ABC＝bcsin A＝×4×＝2.
答案：2
7．在△ABC中，a＝4，b＝5，c＝6，则＝________．
解析：由余弦定理：cos A＝＝＝，
所以sin A＝，cos C＝＝＝，
所以sin C＝，所以＝＝1.
答案：1
8．已知△ABC的周长为＋1，面积为sin C，且sin A＋sin B＝sin C，则角C的值为________．
解析：将sin A＋sin B＝sin C利用正弦定理化简得：
a＋b＝c，因为a＋b＋c＝＋1，
所以c＋c＝＋1，即c＝1，所以a＋b＝，
因为S△ABC＝absin C＝sin C，所以ab＝.
因为cos C＝＝
＝＝＝，则C＝.
答案：
9．(2017·高考北京卷)在△ABC中，∠A＝60°，c＝a.
(1)求sin C的值；
(2)若a＝7，求△ABC的面积．
解：(1)在△ABC中，因为∠A＝60°，c＝a，
所以由正弦定理得sin C＝＝×＝.
(2)因为a＝7，所以c＝×7＝3.
由余弦定理a2＝b2＋c2－2bccos A得72＝b2＋32－2b×3×，
解得b＝8或b＝－5(舍)．
所以△ABC的面积S＝bcsin A＝×8×3×＝6.
10．(2018·贵州省适应性考试)设△ABC的内角A，B，C所对的边分别为a，b，c，且acos B＝4，bsin A＝3.
(1)求tan B及边长a的值；
(2)若△ABC的面积S＝9，求△ABC的周长．
解：(1)在△ABC中，acos B＝4，bsin A＝3，
两式相除，有＝＝tan B＝，
又acos B＝4，所以cos B>0，则cos B＝，故a＝5.
(2)由(1)知，sin B＝，由S＝acsin B＝9，得c＝6.
由b2＝a2＋c2－2accos B＝13，得b＝.
故△ABC的周长为11＋.

1．(2018·长沙市统一模拟考试)△ABC中，C＝，AB＝3，则△ABC的周长为(　　)
A．6sin＋3 B．6sin＋3
C．2sin＋3 D．2sin＋3
解析：选C.设△ABC的外接圆半径为R，则2R＝＝2，于是BC＝2Rsin A＝2sin A，AC＝2Rsin B＝2sin，于是△ABC的周长为2[sin A＋sin]＋3＝2sin＋3.选C.
2．(2018·安徽江南十校联考)设△ABC的面积为S1，它的外接圆面积为S2，若△ABC的三个内角大小满足A∶B∶C＝3∶4∶5，则的值为(　　)
A. B.
C. D.
解析：选D.在△ABC中，A＋B＋C＝π，
又A∶B∶C＝3∶4∶5，所以A＝，B＝，C＝π.
由正弦定理＝＝＝2R(a、b、c为△ABC中角A、B、C的对边，R为△ABC的外接圆半径)可得，a＝·c，b＝·c，R＝.
所以S1＝absin C＝···c2·sin C
＝sin A·sin B·sin C·，
S2＝πR2＝·，
所以＝＝＝，故选D.
3．如图，在四边形ABCD中，已知AD⊥CD，AD＝10，AB＝14，∠BDA＝60°，∠BCD＝135°，则BC的长为________．

解析：在△ABD中，设BD＝x，则
BA2＝BD2＋AD2－2BD·AD·cos∠BDA，
即142＝x2＋102－2·10x·cos 60°，
整理得x2－10x－96＝0，
解得x1＝16，x2＝－6(舍去)．
在△BCD中，由正弦定理：＝，所以BC＝·sin 30°＝8.
答案：8
4．在△ABC中，角A、B、C的对边分别是a、b、c，＝a，a＝2.若b∈[1，3]，则c的最小值为________．
解析：由＝a，得＝sin C．由余弦定理可知cos C＝，即3cos C＝sin C，所以tan C＝，故cos C＝，所以c2＝b2－2b＋12＝(b－)2＋9，因为b∈[1，3]，所以当b＝时，c取最小值3.
答案：3
5.(2018·洛阳市第一次统一考试)如图，平面四边形ABDC中，∠CAD＝∠BAD＝30°.
(1)若∠ABC＝75°，AB＝10，且AC∥BD，求CD的长；
(2)若BC＝10，求AC＋AB的取值范围．
解：(1)由已知，易得∠ACB＝45°，
在△ABC中，＝⇒BC＝5.
因为AC∥BD，所以∠ADB＝∠CAD＝30°，∠CBD＝∠ACB＝45°，
在△ABD中，∠ADB＝30°＝∠BAD，所以DB＝AB＝10.
在△BCD中，CD＝＝5.
(2)AC＋AB>BC＝10，
cos 60°＝⇒(AB＋AC)2－100＝3AB·AC，
而AB·AC≤，
所以≤，
解得AB＋AC≤20，
故AB＋AC的取值范围为(10，20]．
6．已知a，b，c分别是△ABC中角A，B，C的对边，acsin A＋4sin C＝4csin A.
(1)求a的值；
(2)圆O为△ABC的外接圆(O在△ABC内部)，△OBC的面积为，b＋c＝4，判断△ABC的形状，并说明理由．
解：(1)由正弦定理可知，sin A＝，sin C＝，
则acsin A＋4sin C＝4csin A⇔a2c＋4c＝4ac，
因为c≠0，所以a2c＋4c＝4ca⇔a2＋4＝4a⇔(a－2)2＝0，可得a＝2.
(2)设BC的中点为D，则OD⊥BC，
所以S△OBC＝BC·OD.
又因为S△OBC＝，BC＝2，
所以OD＝，
在Rt△BOD中，tan∠BOD＝＝＝＝，
又0°<∠BOD<180°，所以∠BOD＝60°，
所以∠BOC＝2∠BOD＝120°，
因为O在△ABC内部，
所以∠A＝∠BOC＝60°，
由余弦定理得a2＝b2＋c2－2bccos A.
所以4＝b2＋c2－bc＝(b＋c)2－3bc，又b＋c＝4，
所以bc＝4，所以b＝c＝2，
所以△ABC为等边三角形．