数学人教版函数复习ppt课件

这是一份数学人教版函数复习ppt课件，共14页。PPT课件主要包含了内容分析，例题精讲，达标训练，本课知识等内容，欢迎下载使用。

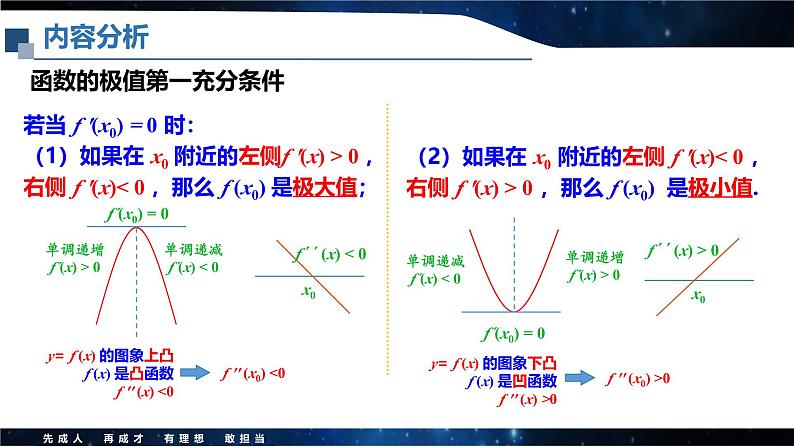
若当 f ′(x0) = 0 时：（1）如果在 x0 附近的左侧f ′(x) > 0 ，右侧 f ′(x)< 0 ，那么 f (x0) 是极大值；（2）如果在 x0 附近的左侧 f ′(x)< 0 ，右侧 f ′(x) > 0 ，那么 f (x0) 是极小值.
函数的极值第一充分条件
【例1】若函数f(x)=x3－ax2－bx+a2在x=1处有极值10，则a－b=（    ）A．6B．－15C．－6或15D．6或－15
若当 f ′(x0) = 0 时：（1）如果在 x0 附近的左侧f ′(x) > 0 ，右侧 f ′(x)< 0 ，那么 f (x0) 是极大值；
（2）如果在 x0 附近的左侧 f ′(x)< 0 ，右侧 f ′(x) > 0 ，那么 f (x0) 是极小值.
y= f (x) 的图象上凸f (x) 是凸函数f ′′ (x) <0
y= f (x) 的图象下凸f (x) 是凹函数f ′′ (x) >0
f ′′ (x0) <0
f ′′ (x0) >0
函数的极值第二充分条件
已知函数y=f (x)在x0处二阶可导．若存在 x0∈[a,b],使得f ′(x0)=0，且f ′′(x0)≠0，则若f ′′(x0) < 0，则y=f (x) 在 x0处取得极大值若f ′′(x0) > 0，则y=f (x) 在 x0处取得极小值
注：f ′′(x0)=0时,函数y=f (x)在 x0处的极值应用第一充分条件处理或者高阶导数处理。
函数的极值第三充分条件
已知函数y=f (x)在x0处存在n阶导数．若存在 x0∈[a,b],使得f ′(x0)=f ′′(x0)=f ′′′(x0)=……=f (n-1)(x0)=0，且f (n)(x0)≠0，则如果n为奇数，x0不是极值点如果n为偶数，x0是极值点。且当f (n)(x0) < 0，则y=f (x) 在 x0处取得极大值，当f (n)(x0) > 0，则y=f (x) 在 x0处取得极小值
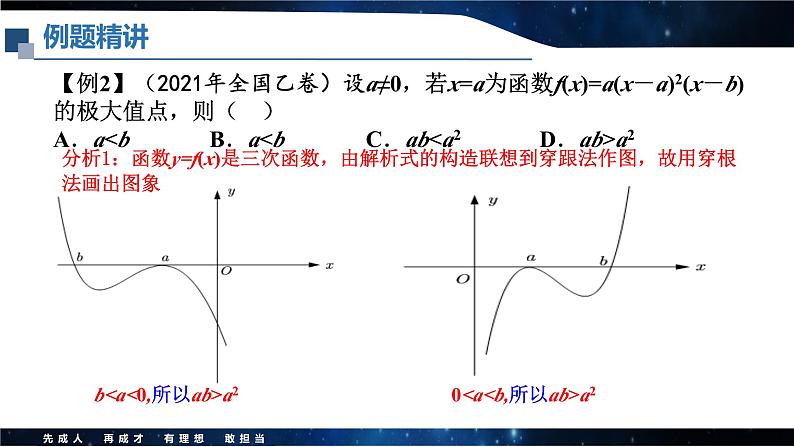
【例2】（2021年全国乙卷）设a≠0，若x=a为函数f(x)=a(x－a)2(x－b)的极大值点，则（    ）A．aa2
分析1：函数y=f(x)是三次函数，由解析式的构造联想到穿跟法作图，故用穿根法画出图象
ba2
0a2
【练习】（2017年全国Ⅲ理科）函数f(x)=x－1－alnx.若f(x)≥0，求a
分析：因为f(x)≥0，可知f(x)min=0，猜根可知f(1)=0，所以f(1)为函数f(x)的极小值也为最小值，所以该问题转化为已知 x=1为函数的极小值，求a
【例3】（2023年全国新高考Ⅱ卷）已知函数f(x)=csax－ln(1－x2),若 x=0是 f(x)的极大值点，求a的取值范围.
由1－x2>0,得－1利用极值第二充分条件解决极值问题
第一步：求出一阶导数f ′(x)和二阶导数f ′′(x) 
第二步：利用第二充分条件，一阶导数为f ′(x0)=0，二阶导数为f ′′(x0) > 0，x0为极小值点，二阶导数f ′′(x0) < 0，x0为极大值点.