





初中数学苏科版(2024)七年级上册(2024)第6章 平面图形的初步认识6.2 角教案配套ppt课件
展开1、了解补角、余角,知道同角(或等角)的补角相等, 同角(或等角)的余角相等;2、能利用同角(或等角)的补角相等、同角(或等角)的余角相等的性质进行简单的计算和说理;3、从数学的角度提出问题、理解问题,锻炼克服 困难的意志.重点:理解互为补角、互为余角的定义, 以及补角、余角的性质.难点:运用互为补角和互为余角的定义以及补角、 余角的性质,结合方程的思想解决相关问题.
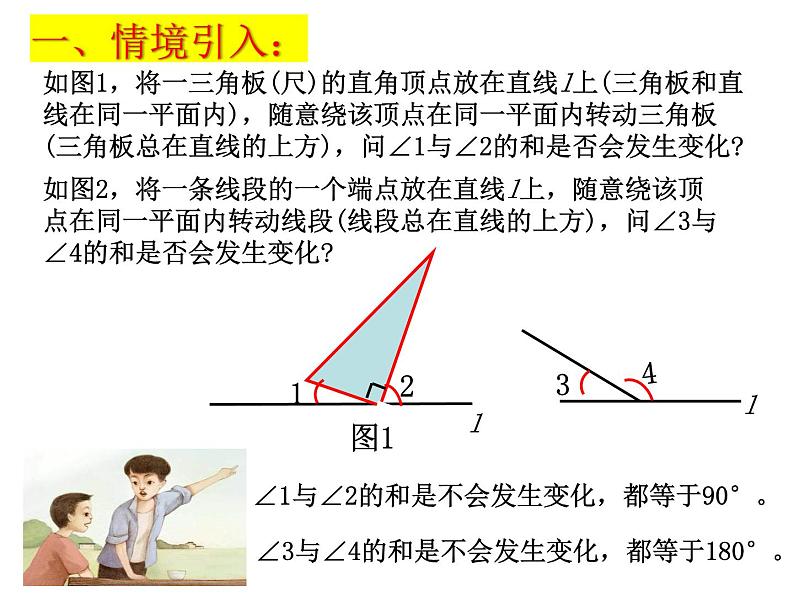
如图1,将一三角板(尺)的直角顶点放在直线l上(三角板和直线在同一平面内),随意绕该顶点在同一平面内转动三角板(三角板总在直线的上方),问∠1与∠2的和是否会发生变化?
如图2,将一条线段的一个端点放在直线l上,随意绕该顶点在同一平面内转动线段(线段总在直线的上方),问∠3与∠4的和是否会发生变化?
∠1与∠2的和是不会发生变化,都等于90°。
∠3与∠4的和是不会发生变化,都等于180°。
如果两个角的度数之和等于180°,那么这两个角互为补角(supplementary angle),简称互补.例如,∠1=60°,∠2=120°,则∠1和∠2互为补角.
如果两个角的度数之和等于90°,那么这两个角互为余角(cm-plementary angle),简称互余.例如,∠3=20°,∠4=70°,则∠3和∠4互为余角.
1、90度的角叫余角,180度的角叫补角. ( )
3、如果一个角有补角,那么这个角一定是钝角.( )
4、互补的两个角不可能相等。 ( )
2、若 ( )
如果∠a与∠β互为补角,∠α与∠r互为补角,那么∠β与∠r有怎样的数量关系?
因为 ∠α与 ∠β互为补角,即∠a+∠β= 180°,
同理,∠r=180°-∠a.
于是,我们得到如下结论:
同角(等角)的补角相等.
类似地,可以得到:同角(等角)的余角相等.
所以 ∠β=180°-∠a.
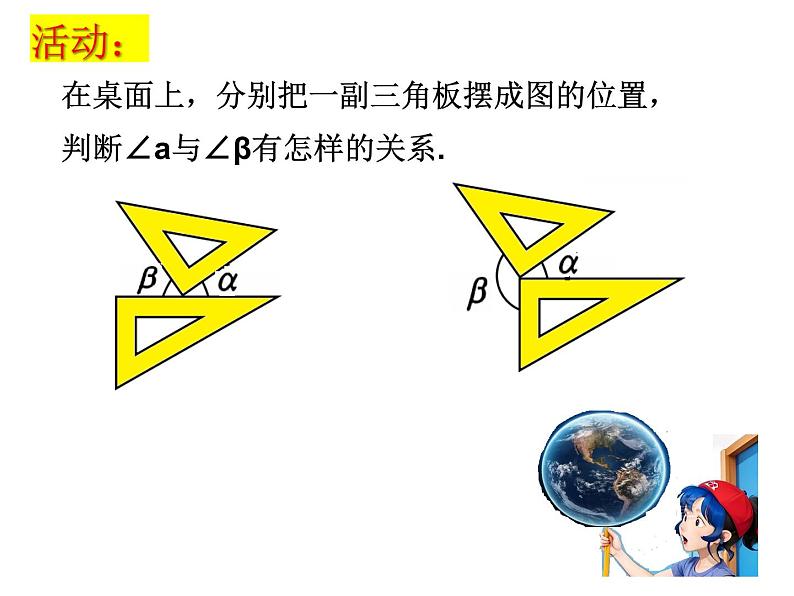
在桌面上,分别把一副三角板摆成图的位置,判断∠a与∠β有怎样的关系.
例2、已知∠α与∠β互为补角,且∠β比∠α 大30°.求∠a,∠β的大小.
解:根据题意,得∠β=∠a+30°.
因为 ∠α与 ∠β互为补角,即∠α+∠β=180°,
所以 ∠a+(∠a+30°)=180°.
所以 ∠α = 75°, ∠β= 75°+30°= 105°.
已知一个角的补角是这个角的余角的4倍,求这个角的度数。
解:设这个角为x°,则它的余角为(90-x) °, 它的补角为(180-x) °,得 180-x=4(90-x) 180-x=360-4x -x+4x=360-18 3x=180 x=60 答:这个角是60°.
(1)钝角没有余角,但一定有补角。 ( )
(2)互余的两个角一定都是锐角,两个锐角一定互余.( )
(3)如果 ( )
(4)如果 ( )
2.如图,∠AOB与∠BOC互为余角,∠BOC与∠COD互为余角. 若∠AOD=126°,则∠BOC 的大小为 ( ) A.36° B. 44° C.54° D.63°
4.已知∠α=73°.求∠a 的补角和余角.5. 如图,/AOC与∠COB互为余角,∠COB 与∠BOD 互为余角,∠BOC=52°.求∠AOD 的大小.
3.下列说法正确的是 ( ) A.互补的两个角一定是一个锐角和一个钝角 B.在三角形中,互余的两个角一定都是锐角 C.平角就是一条直线 D.若∠A+∠B+∠C=180°,则∠A,∠B,∠C三角互补
想一想,同一个锐角的补角与它的余角之间有怎样的数量关系?
同一个锐角的补角比它的余角多90°。
方向角是指正北(或正南)方向线与目标方向线之间所夹的角,如图中射线OC表示北偏西25°方向.
用量角器或三角尺画出表示下列方向的射线(1)北偏东60°方向(2)南偏西75°方向(3)东北方向
(1)如图①,将一副直角三角尺的直角顶点重合在点O处,①∠AOD与∠BOC的数量关系是 ;②∠AOC与∠BOD的数量关系是 。(2)若将这副直角三角尺按如图②所示的方式摆放,使三角尺的直角顶点重合在点O处∠AOD与∠BOC有什么数量关系?∠AOC与∠BOD又有什么数量关系?请分别说明理由.
同角或等角的补角相等.
∠ (0 ° <∠ < 90 °)的余角是 , ∠ 的补角是 .则一个锐角的补角比它的余角大 .
1.甲从点O出发,沿北偏西30°方向走了50m到达A点,乙也从O点出发,沿南偏东35°方向走了80m,那么∠AOB等于( ) A、65° B、115° C、175° D、185°
2、3点半,钟表的时针与分针所成的锐角是( ) A、70° B、75° C、85° D、90°★3、时钟的分针从4点整的位置,经过多长时间与时针第一次重合?
5.已知一条射线OA,若从点0再引两条射线OB和OC, 使∠AOB=80°,∠BOC=30.求∠AOC的度数.
初中苏科版6.3 余角 补角 对顶角教案配套ppt课件: 这是一份初中苏科版6.3 余角 补角 对顶角教案配套ppt课件,共27页。PPT课件主要包含了学习目标,对顶角,图中还有哪些对顶角,即学即练,∠FOB,∠COE,你是怎样得到的,对顶角的性质,变式训练,均为90°等内容,欢迎下载使用。
苏科版七年级上册6.3 余角 补角 对顶角集体备课课件ppt: 这是一份苏科版七年级上册6.3 余角 补角 对顶角集体备课课件ppt,共21页。PPT课件主要包含了学习目标,导入新课,情境引入,讲授新课,余角和补角的概念,典例精析,练一练,°37′,观察与思考,90-x°等内容,欢迎下载使用。
初中数学苏科版七年级上册第6章 平面图形的认识(一)6.3 余角 补角 对顶角示范课课件ppt: 这是一份初中数学苏科版七年级上册第6章 平面图形的认识(一)6.3 余角 补角 对顶角示范课课件ppt,共35页。PPT课件主要包含了教学目标,做一做,试一试,这两个概念的区别,议一议,x2+2x,天平仍然平衡,天平两边同时,代数式,等式的基本性质1等内容,欢迎下载使用。














