



- 1.1 正数与负数的含义(第1课时)(课件)-2024-2025学年七年级数学上册 (沪科版2024) 课件 0 次下载
- 1.1 正数和负数(第2课时 有理数的分类)(课件)-2024-2025学年七年级数学上册 (沪科版2024) 课件 0 次下载
- 1.2数轴、相反数和绝对值(第1课时 数轴)(课件)-2024-2025学年七年级数学上册 (沪科版2024) 课件 0 次下载
- 1.2数轴、相反数和绝对值(第2课时 相反数)(课件)-2024-2025学年七年级数学上册 (沪科版2024) 课件 0 次下载
- 1.3 有理数的大小 课件 2024-2025学年七年级数学上册 (沪科版2024) 课件 0 次下载
初中数学沪科版(2024)七年级上册(2024)1.2 数轴、相反数和绝对值授课ppt课件
展开目录/CONTENTS
1.理解绝对值的概念及其几何意义;(难点、重点)2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.(难点)
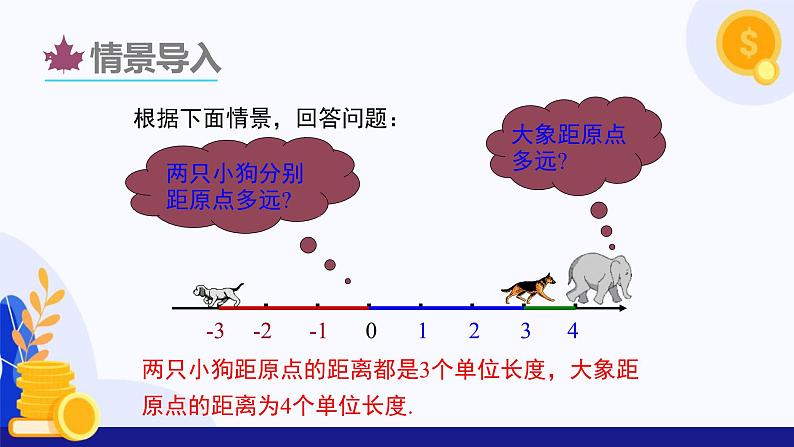
根据下面情景,回答问题:
两只小狗距原点的距离都是3个单位长度,大象距原点的距离为4个单位长度.
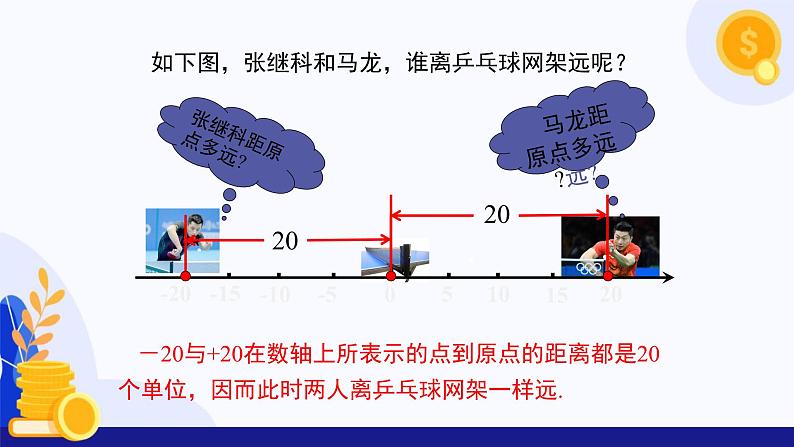
马马龙距原点多远?远?
-20与+20在数轴上所表示的点到原点的距离都是20个单位,因而此时两人离乒乓球网架一样远.
如下图,张继科和马龙,谁离乒乓球网架远呢?
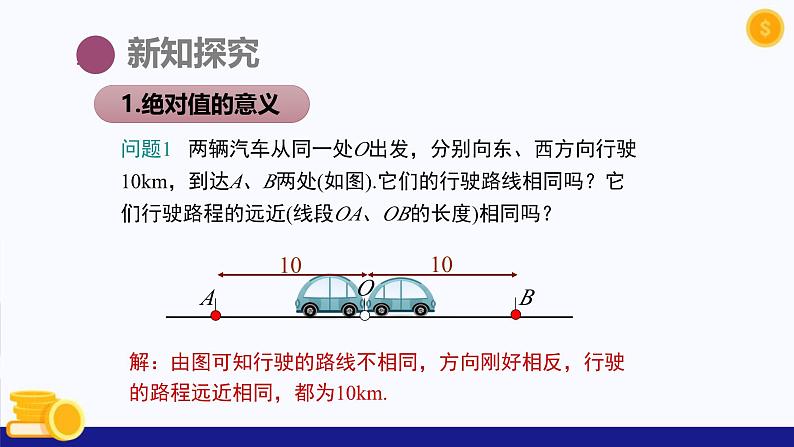
问题1 两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
解:由图可知行驶的路线不相同,方向刚好相反,行驶的路程远近相同,都为10km.
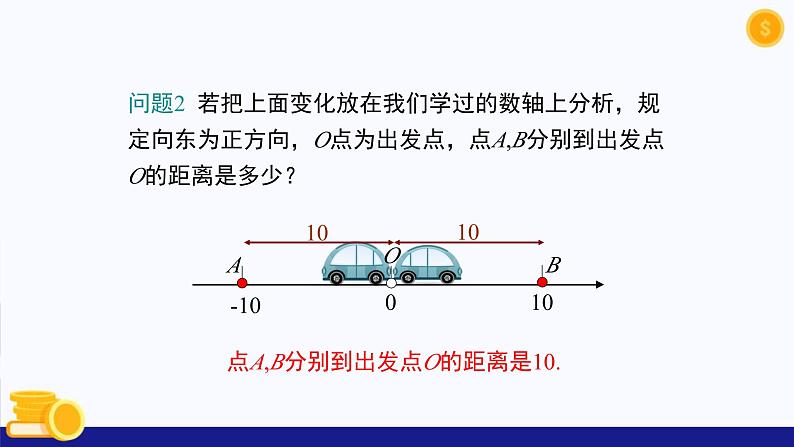
问题2 若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,点A,B分别到出发点O的距离是多少?
点A,B分别到出发点O的距离是10.
问题3 -10与10是相反数,把它们在数轴上表示出来,它们有什么相同之处和不同之处?
-10与10在数轴上所表示的点到原点的距离都是8个单位长度,它们的符号不同,互为相反数.
想一想:互为相反数的两个数到原点的距离都相等吗?
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.互为相反数的绝对值相等.如-10和10的绝对值是10.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
如果a表示有理数,那么│a│有什么含义?
答: ∣a∣表示数a的绝对值;
∣a∣表示数轴上数a对应的点与原点的距离.
1.怎样表示a的相反数?2.互为相反数的两个数的绝对值又有什么关系呢?
3.若|a|= |b|,则a与b有什么关系?
1.表示+7的点与原点的距离是 个单位长度,即+7的绝值是___,记作 ; 2.表示2.8的点与原点的距离是 个单位长度,即2.8的绝对值是____,记作 ; 3.表示0的点与原点的距离是 个单位长度,即0的绝对值是_____,记作 ; 4. 表示-6的点与原点的距离是 个单位长度,即-6的绝对值是_____,记作 ;
5. [新考法 定义法]如图,点 A 所表示的数的绝对值是 ( A )
因为点 A 表示的数是-3,所以点 A 所表示的数的绝 对值是3.
6. [新考法·数形结合法 2023·长春]数 a , b , c , d 在数轴上 对应点的位置如图所示,这四个数中绝对值最小的是 ( B )
问题 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0,即 |0|=0
而 原点到原点的距离是0
思考:因为正数可用a>0表示,负数可用a<0表示,那么上述三条可怎么表述呢?
(1)如果a>0,那么|a|=a; (2)如果a<0,那么|a|=-a; (3)如果a=0,那么|a|=0.
例1(课本例3)求下列各数的绝对值:
|-0.1| = 0.1,
正数的绝对值是它本身,负数的绝对值是它的相反 数,因此解此类题要考虑全面,不要丢解.
8. [2024·重庆一中模拟]数 a 在数轴上的对应点在原点左边, 且| a |=4,则 a 的值为( C )
因为数 a 在数轴上的对应点在原点左边,所以 a <0. 又因为| a |=4,所以 a =-4.
9. 若| a |=- a ,则在下列选项中, a 不可能是( D )
因为| a |=- a ,
所以 a 不可能是正数.
10. 有理数中绝对值等于它本身的数是( D )
有理数中绝对值等于它本身的数是正数和0,即非负 数.故选D.
例2. 已知|x |=2,| y |=3,且 x < y,求 x ,y .
[解析] 由绝对值的定义知 x=±2,y=±3,再由x < y 决定 x,y 的值.
解:因为|x |=2,|y |=3,所以 x =± 2,y =± 3.又因为x < y,所以x = 2,y = 3 或x =-2,y =3.
解:根据题意可知x-4=0,y-3=0,所以x=4,y=3,故x+y=7.
【归纳】 几个非负数的和为0,则这几个数都为0.
解析: 一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
例4.[新考法 非负性求最值法]已知| x |是非负数,且非负 数中最小的数是0.(1)当 x = 时,| x -2 026|有最小值,这个最 小值是 ;(2)当 x = 时,2 026-| x -1|有最大值,这个最 大值是 .
易错点 忽略0也是绝对值等于其相反数的数而致错11. [新考法 逆向思维法]如果| x -2|=2- x ,那么 x 的取 值范围是( A )
本题易漏掉“0”这个特殊数 .因为当 a >0时,| a |= a ;当 a <0时,| a |=- a ;当 a =0时,| a | = a =- a ,所以当 a ≤0时,| a |=- a .因为| x - 2|=2- x ,所以 x -2≤0,所以 x ≤2.
12. [新视角 结论探究题]观察比较:|2|=2,|-2|=2,|3|=3,|-3|= 3,…,| x |= x ,|- x |= x ( x ≥0).(1)若| a |=2,则 a = ;若| a |=0,则 a = ;若| a |=5,则 a = .
(2) a , b 表示任意有理数,若| a |=| b |,则 a 与 b 之间有什么关系?
【解】 a =± b .
13. [新考向 知识情境化]一条直线流水线上依次有5个机器 人,它们站的位置在数轴上依次用点 A1, A2, A3, A4, A5表示,如图.
(1)站在点 上的机器人表示的数的绝对值最大,站 在点 和点 ,点 和点 上的 机器人表示的数的绝对值相等.
因为|-4|最大,所以站在点 A1上的机器人表 示的数的绝对值最大.因为|-3|=|3|,|-1| =|1|,所以站在点 A2和点 A5,点 A3和点 A4上的机 器人表示的数的绝对值相等.
(2)怎样将点 A3移动,使它先到达点 A2,再到达点 A5, 请用文字语言说明.
【解】将点 A3先向左移动2个单位长度到达点 A2,再向右移动6个单位长度到达点 A5.
(3)若原点是零件供应点,则5个机器人分别到达供应点 取货的总路程是多少?
【解】|-4|+|-3|+|-1|+|1|+|3|=12.
答:5个机器人分别到达供应点取货的总路程是12.
14. 同学们都知道,|5-(-2)|表示5与-2之差的绝对 值,实际上也可理解为5与-2两数在数轴上所对应的两 点之间的距离.试探索:(1)|5-(-2)|= .
(2)猜想:对于任意有理数 x ,| x -(-6)|+| x -3| 是否有最小值?如果有,求出最小值;如果没有,说 明理由.
【解】有最小值.因为| x -(-6)|表示数轴上 x 所对应的点到-6所对应的点的距离,| x -3|表示数轴上 x 所对应的点到3所对应的点的距离,所以| x -(-6)|+| x -3|表示数轴上 x 所对应的点到-6和3所对应的两点的距离之和,所以当 x 所对应的点在-6和3所对应的两点之间(包括端点)时,| x -(-6)|+| x -3|有最小值,最小值为9.
(1)如果a>0,那么|a|=a; (2)如果a<0,那么|a|=-a; (3)如果a=0,那么|a|=0.a为有理数
1.在数轴上表示出下列各点,并分别指出它们的绝对值:
3.下列等式中不成立的是( )
2.写出一个正数、两个负数,指出它们的相反数,并把它们在数轴上表示出来.
解:答案不唯一.如+4,-3,-1.5;+4的相反数为-4,-3的相反数为+3,-1.5的相反数为+1.5.在数轴上表示如图所示.
3.下列每题的各对数中,哪些是相等的,哪些互为相反数?(1)+(-4)与-(+4);(2)-(-4)与-4;(3)+(+4)与-(-4);(4)-(+4)与-(-4).
解:相等的为(1)(3),互为相反数的为(2)(4).
4.求下列各数的绝对值: -25,0.08,-7,1.5,0, .
解:绝对值分别为25,0.08,7,1.5,0, .
5.(1)绝对值是5的数有几个,各是多少? (2)绝对值是0的数有几个? (3)是否存在绝对值是-4的数,为什么?
解:有两个,分别是+5,-5.
解:不存在,因为绝对值具有非负性,即|a|≥0.
6.在数轴上分别表示出绝对值是3,1.5,0的数.
解:如图所示,点A、B表示绝对值是3的数,点C、D表示绝对值是1.5的数,点E表示绝对值是0的数.
7.在数轴上点A表示的数是-3,与点A距离2个单位长度的点表示的数是什么?
814,812,809,807,808.
解:第三次测得的结果最接近设计长度,由绝对值的意义可知第三次测得的数据与设计长度的差的绝对值最小.
8.一座桥梁的设计长度为810 m,建成后,测量了5次,测得的数据是(单位:m):814,812,809,807,808.如果以设计长度为基准,试用正负数表示各次测得的数值与设计长度的差(填表).哪次测得的结果最接近设计长度?你说的最接近是根据什么说的?
2.正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下:指出哪个排球的质量好一些,并用绝对值的知识加以说明.
利用绝对值检测产品质量.
【规范解答】解:第五个排球的质量好一些,因为它的绝对值最小,也就是离标准质量的克数最近.
【思路分析】检测产品质量的优劣,关键要看偏差的绝对值大小,而与数据的符号无关.偏差的绝对值越小,越接近标准值.
初中数学沪科版(2024)七年级上册(2024)1.2 数轴、相反数和绝对值说课课件ppt: 这是一份初中数学沪科版(2024)七年级上册(2024)<a href="/sx/tb_c4053944_t3/?tag_id=26" target="_blank">1.2 数轴、相反数和绝对值说课课件ppt</a>,共20页。PPT课件主要包含了旧知回顾,绝对值的意义,知识归纳,求下列各数的绝对值,﹢11,-37,非负数,-10,和-5,和-2等内容,欢迎下载使用。
初中1.2 数轴、相反数和绝对值课前预习ppt课件: 这是一份初中<a href="/sx/tb_c4053944_t3/?tag_id=26" target="_blank">1.2 数轴、相反数和绝对值课前预习ppt课件</a>,共20页。PPT课件主要包含了复习回顾,情景导入,推进新课,﹣15,﹣65,随堂练习等内容,欢迎下载使用。
沪科版(2024)七年级上册(2024)第1章 有理数1.2 数轴、相反数和绝对值多媒体教学ppt课件: 这是一份沪科版(2024)七年级上册(2024)<a href="/sx/tb_c4053944_t3/?tag_id=26" target="_blank">第1章 有理数1.2 数轴、相反数和绝对值多媒体教学ppt课件</a>,共16页。PPT课件主要包含了新课导入,推进新课,还有0,﹢11,﹣88,随堂练习,拓展延伸等内容,欢迎下载使用。













