人教B版高中数学必修第一册第3章3-1-3第2课时函数奇偶性的应用课件

这是一份人教B版高中数学必修第一册第3章3-1-3第2课时函数奇偶性的应用课件，共35页。

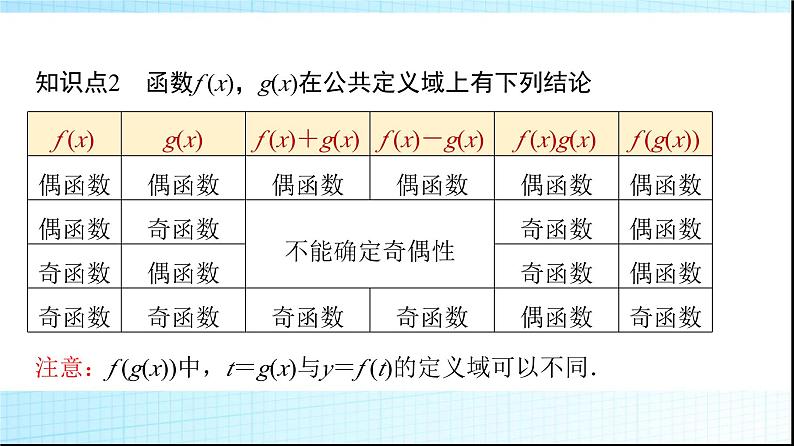
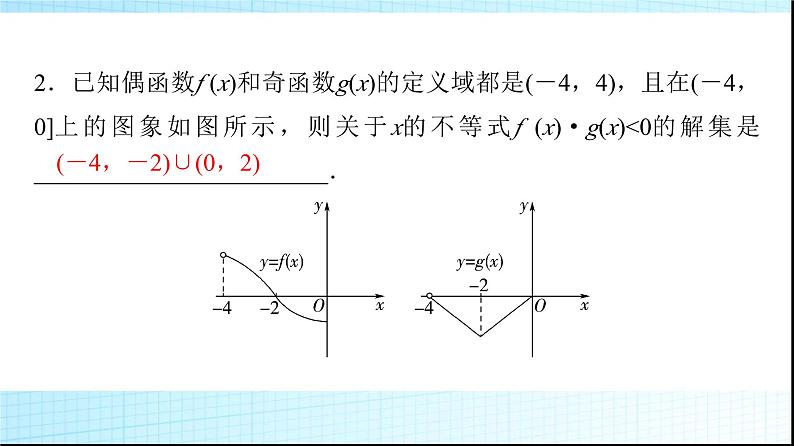
第2课时　函数奇偶性的应用第三章　函数3.1　函数的概念与性质3.1.3　函数的奇偶性必备知识·情境导学探新知 图①　　图②知识点1　函数的单调性与奇偶性(1)若f (x)为奇函数且在区间[a，b](a＜b)上为增函数(减函数)，则f (x)在[－b，－a]上为______(减函数)，即在关于原点对称的区间上单调性____．(2)若f (x)为偶函数且在区间[a，b](a＜b)上为增函数(减函数)，则f (x)在[－b，－a]上为______(增函数)，即在关于原点对称的区间上单调性____．增函数相同减函数相反知识点2　函数f (x)，g(x)在公共定义域上有下列结论注意：f (g(x))中，t＝g(x)与y＝f (t)的定义域可以不同．1．定义在R上的偶函数f (x)在(0，＋∞)上是增函数，则f (－4)，f (－π)，f (3)的大小关系为________________________．(用“<”表示)f (3)＜f (－π)＜f (－4)　[∵f (x)是定义在R上的偶函数，∴f (－π)＝f (π)，f (－4)＝f (4)，又f (x)在(0，＋∞)上是增函数，0＜3＜π＜4，∴f (3)＜f (π)＜f (4)，即f (3)＜f (－π)＜f (－4)．]f (3)＜f (－π)＜f (－4)2．已知偶函数f (x)和奇函数g(x)的定义域都是(－4，4)，且在(－4，0]上的图象如图所示，则关于x的不等式f (x)·g(x)<0的解集是________________________．(－4，－2)∪(0，2)(－4，－2)∪(0，2)　[设h(x)＝f (x)g(x)，则h(－x)＝f (－x)g(－x)＝－f (x)g(x)＝－h(x)，所以h(x)是奇函数，由图象可知：当－40，g(x)<0，即h(x)<0，当00，即h(x)<0，所以h(x)<0的解集为(－4，－2)∪(0，2)．]关键能力·合作探究释疑难   反思领悟　利用函数奇偶性求函数解析式的步骤(1)“求谁设谁”，即在哪个区间上求解析式，x就应在哪个区间上设．(2)转化到已知区间上，代入已知的解析式．(3)利用f (x)的奇偶性写出－f (x)或f (－x)，从而解出f (x)．提醒：若函数f (x)的定义域内含0且为奇函数，则必有f (0)＝0，但若为偶函数，未必有f (0)＝0．[跟进训练]1．已知函数f (x)是定义在(－∞，＋∞)上的偶函数，当x∈(－∞，0)时，f (x)＝x－x4，则当x∈(0，＋∞)时，f (x)＝________．－x－x4　[当x∈(0，＋∞)时，－x∈(－∞，0)，∴f (－x)＝－x－(－x)4＝－x－x4，又∵f (x)是定义在(－∞，＋∞)上的偶函数，∴f (x)＝f (－x)＝－x－x4．]－x－x4类型2　利用单调性与奇偶性比较大小【例2】　已知定义在R上的奇函数f (x)满足f (x－4)＝－f (x)，且在区间[0，2]上单调递增，则(　　)A．f (－1)f (0)，即f (1)>0，所以f (3)＝f (1)>0，f (－1)＝－f (1)<0，于是f (－1)0，则当n∈N+时，有(　　)A．f (－n)0，∴若x2－x1>0，则f (x2)－f (x1)>0，即若x2>x1，则f (x2)>f (x1)，若x2－x1<0，则f (x2)－f (x1)<0，即若x2n>n－1≥0，∴f (n＋1)1或a<－2．故选C．][跟进训练]3．函数f (x)是定义在实数集上的偶函数，且在[0，＋∞)上是增函数，f (3)1　　　　　　　　　 B．a<－2C．a>1或a<－2 D．－1f (1)，则|1－x|<1，即－1<1－x<1，故0f (1)的x的取值范围是(　　)A．(0，2)　　　　　　　 B．(－∞，1)C．(1，＋∞) D．(－∞，0)∪(0，2)23题号41x(x－1)　[当x<0时，－x>0，则f (－x)＝x(1－x)．又f (x)是R上的奇函数，所以当x<0时，f (x)＝－f (－x)＝－x(1－x)＝x(x－1)．]3．已知f (x)是R上的奇函数，当x>0时，f (x)＝－x(1＋x)，当x<0时，f (x)＝________．x(x－1)23题号41[1，3]　[∵函数f (x)在(－∞，＋∞)上单调递减，且为奇函数，f (1)＝－1，∴f (－1)＝－f (1)＝1，由－1≤f (x－2)≤1，得－1≤x－2≤1，∴1≤x≤3．]4．函数f (x)在(－∞，＋∞)上单调递减，且为奇函数．若f (1)＝－1，则满足－1≤f (x－2)≤1的x的取值范围是________．[1，3][提示]　已知函数f (x)的奇偶性及函数f (x)在某区间上的解析式，求该函数在整个定义域上的解析式的方法如下：①求哪个区间上的解析式，x就设在哪个区间上；②把x对称转化到已知区间上，代入到已知区间上的函数解析式中；③利用f (x)的奇偶性将f (－x)用－f (x)或f (x)表示，从而求出f (x)．回顾本节知识，自主完成以下问题：1．怎样利用函数奇偶性求函数解析式？[提示]　(1)奇函数在[a，b]和[－b，－a]上具有相同的单调性．(2)偶函数在[a，b]和[－b，－a]上具有相反的单调性．(3)解决不等式问题时一定要充分利用已知的条件，把已知不等式转化成f (x1)>f (x2)或f (x1)