苏教版 (2019)必修 第二册第9章 平面向量9.2 向量运算一等奖课件ppt

这是一份苏教版 (2019)必修 第二册第9章 平面向量9.2 向量运算一等奖课件ppt，共33页。PPT课件主要包含了向量的加法，向量加法的运算律，a+00+aa，向量的减法等内容，欢迎下载使用。

1.借助实例和平面向量的几何表示，掌握平面向量加、减运算及运算规则，理解其几何意义。2.掌握向量加减法的运算律。
上节课我们借助物理中的受力分析，引入了向量的概念。
在物理学中，把木块m放在光滑的斜面上，重力G与斜面支持力N的合力是一个沿着斜面向下的力。所以木块m向下滑动。
思考：如何求木块m的合力呢？
从运算的角度看，求几个力的合力可以看作是对几个向量实施某种运算的结果。换句话说，向量与实数一样也能进行运算。
思考：向量如何进行运算？
物理学中的速度的合成和力的合成都可以看成是向量的加法。
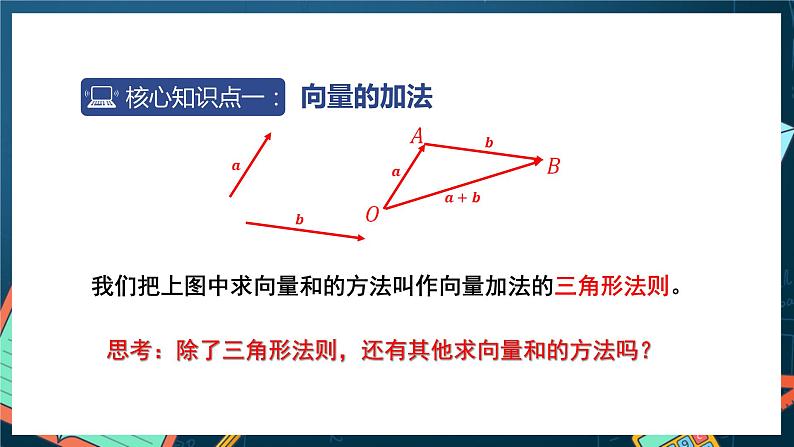
求两个向量和的运算，叫作向量加法。
我们把上图中求向量和的方法叫作向量加法的三角形法则。
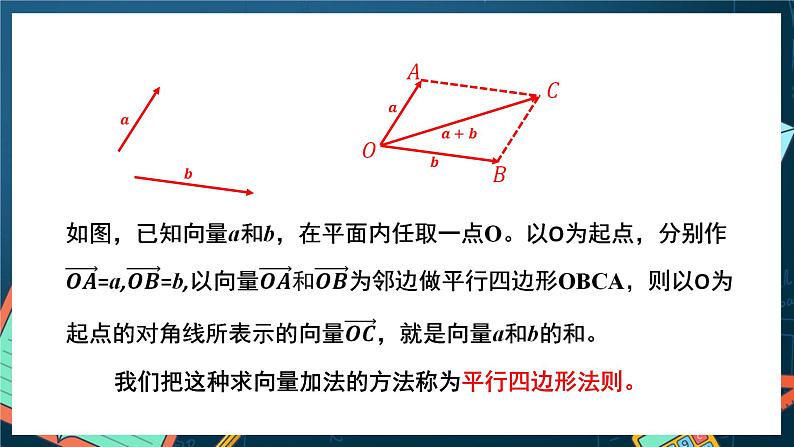
思考：除了三角形法则，还有其他求向量和的方法吗？
我们把这种求向量加法的方法称为平行四边形法则。
规定1：任意向量与其相反向量的和是零向量。即
a+(-a)=(-a)+a=0
规定2：对于零向量和任一向量a，规定：
思考：在实数运算时，我们学过加法的交换律和结合律，那么在向量的加法运算中，是否符合交换律和结合律呢？
我们可以得到：(a+b)+c=a+(b+c)；即向量加法满足结合律。
与实数的减法类似，我们定义，向量的减法是向量加法的逆运算。
若b＋x=a，则向量x叫作a与b的差，记为a-b。求两个向量差的运算，叫作向量的减法。
根据向量减法的定义和向量加法的三角形法则，我们可以得到向量a-b的作图方法。
总结：当向量a，b起点相同时，从b的终点指向a的终点的向量就是a-b。
我们也可以把向量的减法看成向量的加法，即：a-b=a+(-b)
总结：减去一个向量等于加上这个向量的相反向量。
【总结1】向量加法的平行四边形法则和三角形法则的区别和联系
【总结2】向量加法运算律的意义和应用原则
意义：向量加法的运算律为向量加法提供了变形的依据，实现恰当利用向量加法法则运算的目的.实际上，由于向量的加法满足交换律和结合律，故多个向量的加法运算可以按照任意的次序、任意的组合来进行.
应用原则：通过向量加法的交换律，使各向量“首尾相连”，通过向量加法的结合律调整向量相加的顺序.
【总结3】求作两个向量的差向量的两种思路
(1)可以转化为向量的加法来进行，如a－b，可以先作－b，然后作a＋(－b)即可.
(2)可以直接用向量减法的三角形法则，即把两向量的起点重合，则差向量为连接两个向量的终点，指向被减向量的终点的向量.
1.向量的加法：（1）向量加法的三角形法则和四边形法则。（2）向量加法的交换律和结合律。2.向量间的减法：向量减法的法则；