数学九年级上册2 矩形的性质与判定教学ppt课件

这是一份数学九年级上册2 矩形的性质与判定教学ppt课件，共22页。PPT课件主要包含了矩形的判定，矩形具有哪些性质呢，有一个角是直角，平行四边形，矩形的判定方法1，符号语言，对角线相等，三个角是直角，矩形的判定方法等内容，欢迎下载使用。

1.理解并掌握矩形的判定定理，并会用矩形的判定定理进行证明和计算.2.经历矩形判定定理的探索过程，进一步发展合情推理能力.3.能够用综合法证明矩形的判定定理，进一步发展演绎推理能力.4.体会探索与证明过程中所蕴含的抽象、推理等数学思想.
观察下列实物中的矩形，说一说什么是矩形？
有一个角是直角的平行四边形叫做矩形.
AB∥CD且AB=CD；
AD∥BC且AD=BC；
对角线互相平分且相等；
∠A=∠C=∠B=∠D=90°
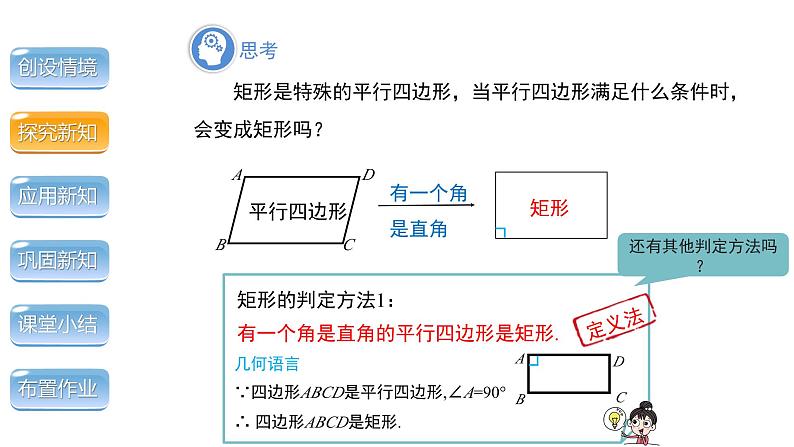
矩形是特殊的平行四边形，当平行四边形满足什么条件时，会变成矩形吗？
有一个角是直角的平行四边形是矩形.
几何语言∵四边形ABCD是平行四边形,∠A=90° ∴ 四边形ABCD是矩形.
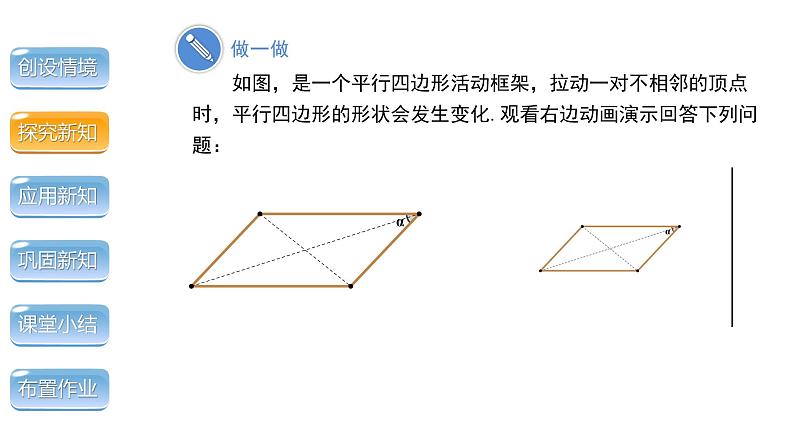
如图，是一个平行四边形活动框架，拉动一对不相邻的顶点时，平行四边形的形状会发生变化.观看右边动画演示回答下列问题：
猜想：对角线相等的平行四边形是矩形.
(1)随着∠α 的变化两条对角线的长度将发生怎样的变化？
(2)当两条对角线的长度相等时平行四边形有什么特征？由此你能得到一个怎样的猜想？
随着∠α 的变化两条对角线的长度一条变长，另一条变短.
当两条对角线长度相等时，平行四边形内的∠α 是直角.
已知：四边形ABCD是平行四边形，对角线AC与BD相交于点O，AC=BD.求证：四边形ABCD是矩形.
证明：∵四边形ABCD是平行四边形∴AB=DC，AB∥DC.又∵BC = CB，AC = DB，∴△ABC≌△DCB. ∴∠ABC=∠DCB.∵AB∥DC，∴∠ABC+ ∠DCB = 180°.∴∠ABC=∠DCB= 90°.∴□ABCD 是矩形(矩形的定义).
定理：对角线相等的平行四边形是矩形.
∵在□ABCD中，AC=BD，∴□ABCD是矩形.
我们知道，矩形的四个角都是直角.反过来，一个四边形至少有几个角是直角时，这个四边形就是矩形呢？
猜想：三个角是直角的四边形是矩形.
已知：如图，在四边形ABCD中，∠A=∠B=∠C=90°.求证：四边形ABCD是矩形.
证明： ∵∠A =∠B =∠C= 90°,∴∠A+∠B = 180°, ∠B +∠C=180°.∴AD∥BC，AB∥CD.∴四边形 ABCD 是平行四边形.∴四边形 ABCD 是矩形.
定理：三个角是直角的四边形是矩形.
∵在四边形ABCD中，∠A=∠B=∠C=90°.∴四边形ABCD是矩形.
现在你知道如何判定一个四边形为矩形了吗？
如果仅有一根较长的绳子，你有什么方法检查你家(或教室)刚安装的门框是不是矩形？
说一说这样检查的理由？
对角线相等的平行四边形是矩形.
①先用绳子测量四边形的两对边是否相等，相等则是平行四边形.
②再用绳子测量对角线是否相等,相等则是矩形.
例2 如图，在 □ ABCD 中，对角线 AC 和 BD 相交于点 O，△ABO 是等边三角形，AB = 4.求 □ ABCD 的面积.
分析：由平行四边形的性质可得，OA=OC ,OB=OD.
由△ABO 是等边三角形，得OA=OB =AB=4，
再由矩形的性质得∠ABC=90°，从而由勾股定理求出BC的长，即可求出□ ABCD的面积.
从而有AC=BD=2OA=8，所以□ ABCD是矩形.
例2 如图，在 □ ABCD 中，对角线 AC 和 BD 相交于点 O，△ABO 是等边三角形，AB = 4.求 □ ABCD 的面积.
解: ∵四边形 ABCD 是平行四边形,∴OA = OC,OB = OD.又∵△ABO 是等边三角形，∴OA = OB = AB = 4.∴OA = OB = OC = OD = 4.∴AC = BD = 2OA = 2×4 = 8.∴□ABCD 是矩形(对角线相等的平行四边形是矩形).∴∠ABC = 90°(矩形的四个角都是直角).在Rt△ABC中，由勾股定理，得 AB2+BC2 = AC2，
∴S□ABCD = AB·BC = 4× = .
1.已知：如图，在 □ ABCD 中，M 是 AD 边的中点， 且MB = MC. 求证：四边形 ABCD 是矩形.
证明：在□ ABCD 中，AB = CD，M 是 AD 边的中点，∴MA = MD，且 MB = MC，即△ABM≌△DCM，∴∠A =∠D.又∵∠A +∠D = 180°，∴∠A =∠D = 90°.∴四边形 ABCD 是矩形.
2.如图，在△ABC中，AD 为 BC 边上的中线，延长 AD 至 E，使 DE = AD，连接 BE，CE.(1)试判断四边形 ABEC 的形状；(2)当△ABC 满足什么条件时，四边形 ABEC 是矩形？
解:(1)四边形 ABEC 是平行四边形．证明：∵AD为BC边上的中线，∴BD=CD，∵AD=DE，∴四边形ABEC的对角线互相平分，∴四边形ABEC是平行四边形.
(2)当△ABC 满足∠BAC＝90°时,四边形 ABEC 是矩形．理由如下：有一个角是直角的平行四边形是矩形.
3.如图，点 B 在 MN 上，过 AB 的中点 O 作 MN 的平行线，分别交∠ABM 的平分线和∠ABN 的平分线于点 C，D.试判断四边形 ACBD 的形状，并证明你的结论.
证明: ∵CD ∥MN , BC, BD 分别为∠MBA ,∠ABN 的平分线,∴∠ABD ＝∠DBN ＝∠CDB, ∠ABC ＝∠CBM ＝∠DCB,且∠CBD ＝90°, ∴OC＝OB＝OD ＝OA ．∵∠AOD ＝∠COB，∴△AOD ≌△COB,则∠DAO＝∠OBC, AD ∥BC, AD ＝BC,∴四边形 ACBD 为平行四边形．又∵AB ＝ CD ，∴四边形 ACBD 为矩形．
三个角是直角的四边形是矩形.
对角线相等的平行四边形是矩形.
教科书 第16页习题1.5 第3题