初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质说课ppt课件

这是一份初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质说课ppt课件，共11页。PPT课件主要包含了学习目标，重难点，知识回顾，教学过程，探究新知，例题精讲等内容，欢迎下载使用。

1.掌握平行四边形对角线互相平分的性质. 2.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.
重点：掌握平行四边形对角线互相平分的性质.难点：能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明.
上节课我们学习的平行四边形的性质分别是哪些？
解：平行四边形是中心对称图形，两条对角线的交点是它的对称中心、平行四边形对边相等,对角相等、平行四边形的对边平行.
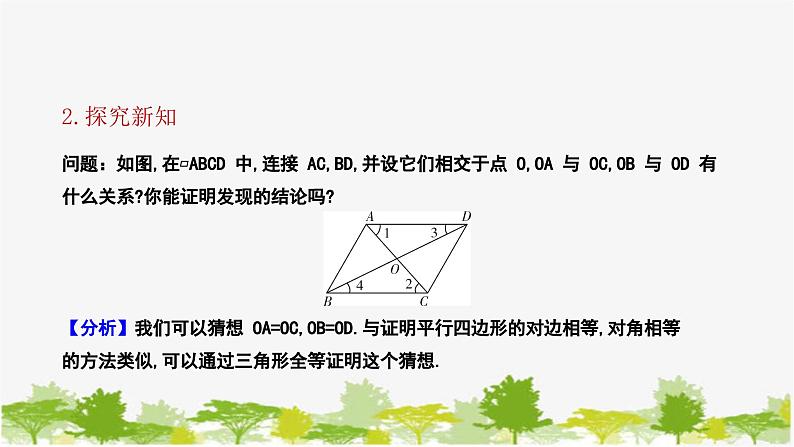
问题：如图,在▱ABCD 中,连接 AC,BD,并设它们相交于点 O,OA 与 OC,OB 与 OD 有什么关系?你能证明发现的结论吗?
【分析】我们可以猜想 OA=OC,OB=OD.与证明平行四边形的对边相等,对角相等的方法类似,可以通过三角形全等证明这个猜想.
解：猜想:OA=OC,OB=OD. 证明:∵ 四边形 ABCD 是平行四边形, ∴ AD∥BC,AD=BC, ∴ ∠1 =∠2,∠3 =∠4. ∴ △AOD≌△COB. ∴OA=OC,OD=OB.
【知识归纳】(1)平行四边形的对角线互相平分. (2)△ABO≌△CDO, △AOD≌△COB, △ABD≌△CDB, △ABC≌△CDA; (3)△ABO、△AOD、△DOC、△COB 的面积相等,且都等于平行四边形面积的四分之一.
例1 如图,平行四边形 ABCD 中,对角线 AC、BD 相交于点 O,AB⊥AC,AB=3,AD=5,求 BD 的长.
证明：∵ 四边形 ABCD 是平行四边形, ∴ BC=AD=5. ∵ AB⊥AC, ∴ △ABC 是直角三角形. ∴ AC= = = 4,AO= AC=2.∴ BO= = = . ∴ BD=2BO=2 .
例2 如图,平行四边形 ABCD 的对角线 AC 与 BD 相交于点 O,过点 O 的直线与 AD, BC 分别相交于点 E、F,求证:OE=OF.
证明：∵ 四边形 ABCD 是平行四边形, ∴ DO=BO,AD∥BC. ∴ ∠ODE=∠OBF. ∵ ∠DOE=∠BOF,∴ △DOE≌△BOF(ASA). ∴ OE=OF.
例3 如图, ▱ABCD 的对角线 AC 与 BD 相交于点O,∠ADB=90°,OA=6,OB=3.求 AD 和 AC 的长度.
解：∵ 四边形 ABCD 是平行四边形, ∴ OA=OC=6,OB=OD=3.∴ AC=2OA=12. 又∵ ∠ADB= 90°, ∴ AD= = = = 3 .
4.巩固练习 完成教材课后同步练习