新疆维吾尔自治区乌鲁木齐市乌鲁木齐八一中学2023-2024学年七年级下学期期中数学试题（原卷版+解析版）

这是一份新疆维吾尔自治区乌鲁木齐市乌鲁木齐八一中学2023-2024学年七年级下学期期中数学试题（原卷版+解析版），文件包含新疆维吾尔自治区乌鲁木齐市乌鲁木齐八一中学2023-2024学年七年级下学期期中数学试题原卷版docx、新疆维吾尔自治区乌鲁木齐市乌鲁木齐八一中学2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

（卷面分值：100分；考试时间：90分钟）
一、选择题（本大题共9小题，共27分）
1. 2的算术平方根是（ ）
A. ±B. -C. D. 4
【答案】C
【解析】
【分析】根据算术平方根的定义即可作答．
【详解】∵，∴2的算术平方根是．
故选C．
【点睛】本题考查了算术平方根定义：一个正数的正的平方根，叫做这个正数的算术平方根，0的算术平方根是0．算术平方根的概念易与平方根的概念混淆而导致错误．弄清概念是解答本题的关键．
2. 在实数，，，，中，无理数有（ ）
A. 个B. 个C. 个D. 个
【答案】C
【解析】
【分析】本题考查了无理数的定义，根据无理数的定义即可判断求解，掌握无理数的定义是解题的关键．
【详解】解：在实数，，，，中，无理数有，，，共个，
故选：．
3. 已知：如图AB∥CD，CE平分∠ACD，∠A=110°，则∠ECD等于
A. 110°B. 70°C. 55°D. 35°
【答案】D
【解析】
【详解】解：∵AB∥CD，∠A=110°，
∴∠ACD=180°-∠A=70
∵CE平分∠ACD，
∴∠ECD=∠ECD=35°
故选D
4. 由可以得到用表示的式子为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】先移项，后系数化为1，即可得．
【详解】解：
移项，得，
系数化为1，得，
故选B．
【点睛】本题考查了方程的基本运算技能，解题的关键是熟练掌握方程的基本运算技能．
5. 如图，下列条件中，能判定的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了平行线的判定定理，根据平行线的判定定理即可作出判断．
【详解】解：A. ，不能判定，故该选项不正确，不符合题意；
B. ∵，∴，故该选项正确，符合题意；
C. ∵，∴，故该选项不正确，不符合题意；
D. ，∴，故该选项不正确，不符合题意；
故选：B．
6. 已知，，则（ ）
A. 35.12B. 351.2C. 111.08D. 1110.8
【答案】A
【解析】
【分析】本题主要考查算术平方根的知识，根据计算得出结论即可．
【详解】解：∵，
∴，
故选：A．
7. 有下列四个命题：一条直线的垂线只有一条；在同一平面内，从一点到某直线的垂线段叫这点到这条直线的距离；如果两条直线垂直，那么他们相交成的四个角都相等；在同一平面内，垂直于同一条直线的两条直线互相平行．其中假命题的个数是（ ）
A. 个B. 个C. 个D. 个
【答案】B
【解析】
【分析】本题考查了命题的真假，根据垂线的性质、点到直线距离、垂直的定义、平行线的判定逐项判断即可求解，掌握有关定义和性质是解题的关键．
【详解】解：一条直线的垂线有无数条，故是假命题；
在同一平面内，从一点到某直线的垂线段的长度叫这点到这条直线的距离，故是假命题；
如果两条直线垂直，那么他们相交成的四个角都相等，故是真命题；
在同一平面内，垂直于同一条直线的两条直线互相平行，故是真命题；
∴假命题有，一共个，
故选：．
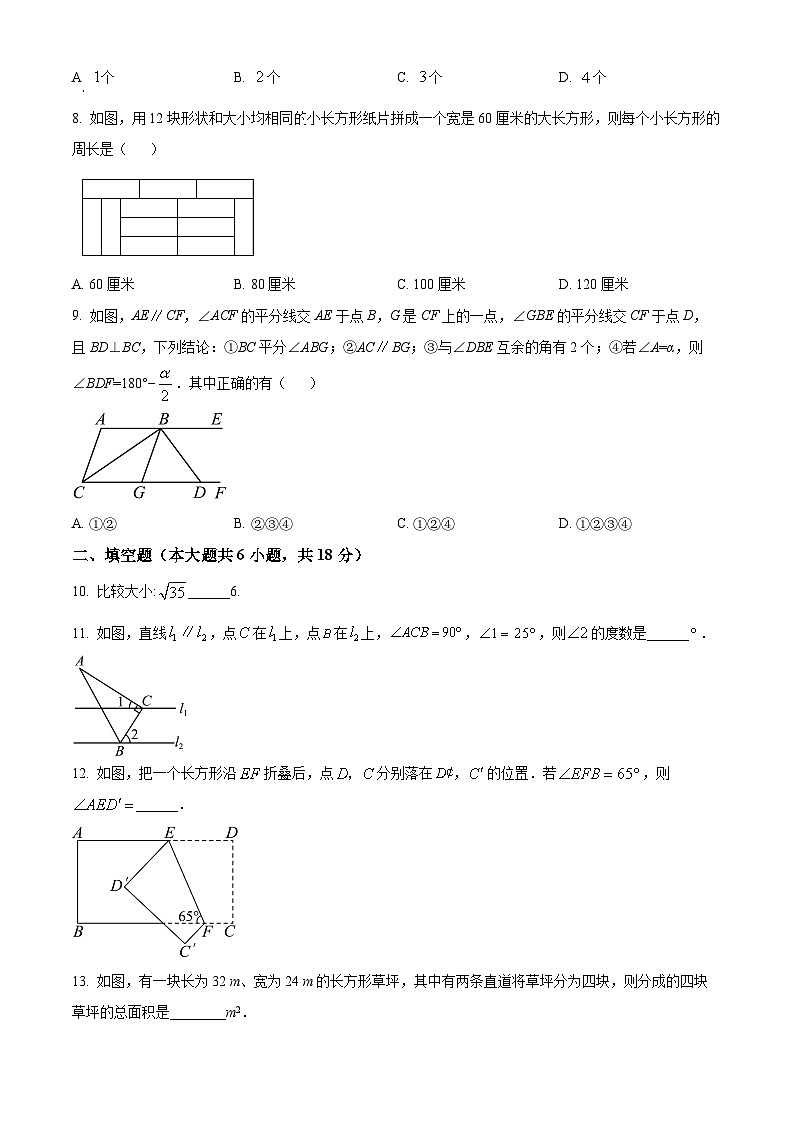
8. 如图，用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形，则每个小长方形的周长是（ ）
A. 60厘米B. 80厘米C. 100厘米D. 120厘米
【答案】D
【解析】
【分析】设小长方形的长为x厘米，小长方形的宽为y厘米，根据题意列出二元一次方程组求解即可；
【详解】设小长方形的长为x厘米，小长方形的宽为y厘米，
根据题意可得：，
解得：，
∴每个小长方形的周长是 （厘米）
故选D．
【点睛】本题主要考查了二元一次方程组的应用，准确计算是解题的关键．
9. 如图，AECF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②ACBG；③与∠DBE互余的角有2个；④若∠A=α，则∠BDF=180°−．其中正确的有（ ）
A. ①②B. ②③④C. ①②④D. ①②③④
【答案】C
【解析】
【分析】根据平行线的性质得出∠A和∠ACB的关系，再根据角平分线的性质找出图中相等的角，由等角的余角相等即可得出结论．
【详解】解：∵CBD=90°，
∴∠ABC+∠EBD=90°，∠CBG+∠DBG=90°，
又∵∠DBG=∠EBD，
∴∠ABC=∠CBG，
∴BC平分∠ABG，故①正确；
∵AECF，
∴∠ABC=∠BCG，
∵BC平分∠ACF，
∴∠ACB=∠BCG，
∵∠ABC=∠CBG，
∴∠CBG=∠ACB，
∴ACBG，故②正确，
∵AECF，
∴∠DBE=∠BDG，
∵∠ABC=∠CBG=∠ACB=∠BCG，∠DBE=∠DBG=∠BDG
∴与∠DBE互余的角有∠ABC，∠GBC，∠ACB，∠GCB，有4个，
故③错误，
∵∠BDF=180°-∠BDG，∠BDG=90°-∠BCG=90°-∠ACB，
又∵∠ACB=×（180°-α）=90°-，
∴∠BDF=180°-[90°-（90°-）]=180°-，故④正确，
综上，正确的有①②④．
故选：C．
【点睛】本题主要考查平行线的性质和判定，关键是要牢记平行线的三个性质，即两直线平行，同位角相等，两直线平行，内错角相等，两直线平行，同旁内角互补．
二、填空题（本大题共6小题，共18分）
10. 比较大小:______6.
【答案】
【解析】
【分析】将6转化成然后再比较大小即可解答.
【详解】解：6=＞ ，
故答案为＜.
【点睛】本题考查了无理数的大小比较，灵活进行转换是解题的关键.
11. 如图，直线，点在上，点在上，，，则的度数是______．
【答案】
【解析】
【分析】本题考查了平行线的性质，由可得，进而由平行线的性质可得，即可求解，掌握平行线的性质是解题的关键．
【详解】解：∵，
∴，
∵，
∴，
∵，
∴，
故答案为：．
12. 如图，把一个长方形沿折叠后，点分别落在，的位置．若，则______．
【答案】##50度
【解析】
【分析】本题考查了平行线的性质，折叠的性质，平角的定义，由平行线的性质可得，由折叠可得，再利用平角的定义即可求解，掌握平行线和折叠的性质是解题的关键．
【详解】解：∵，
∴，
又由折叠可得，，
∴，
故答案为：．
13. 如图，有一块长为32 m、宽为24 m的长方形草坪，其中有两条直道将草坪分为四块，则分成的四块草坪的总面积是________m2．
【答案】660．
【解析】
【详解】解：如图，两条直道分成的四块草坪分别为甲、乙、丙、丁，
把丙和丁都向左平移2米，然后再把乙和丁都向上平移2米，组成一个长方形，长为32－2＝30米，宽为24－2＝22米，所以四块草坪的总面积是30×22＝660（㎡）．
故答案为：660．
【点睛】本题考查了平移的应用，将草坪平移组成一个长方形是解决此题的关键．
14. 已知、满足方程组，则的值为______．
【答案】1
【解析】
【分析】本题考查了二元一次方程组，将两式相减即可得到的值．
【详解】解：，
①②得：，
故答案为：1．
15. 如图，中，，P为直线上一动点，连，则线段的最小值是______．
【答案】
【解析】
【分析】根据垂线段最短，得到当时，的值最小，利用等积法进行计算即可。
【详解】∵点到直线的距离，垂线段最短，
∴当时，的值最小，
在中，
∵，
∴，即：，
∴，
故答案为．
【点睛】本题考查垂线段最短，解题的关键是学会利用面积法求高，属于中考常考题型．
三、解答题（本大题共8小题，共55分）
16. （）计算：；
（）已知，求的值．
【答案】（）；（），．
【解析】
【分析】（）利用算术平方根、立方根的定义，绝对值的性质分别运算，再合并即可求解；
（）利用平方根的定义解答即可求解；
本题考查了实数的运算，利用平方根的定义解方程，掌握实数的运算法则和平方根的定义是解题的关键．
【详解】解：（）原式，
；
（）∵，
∴，
即或，
∴，．
17. 解下列方程组：
（1）；
（2）．
【答案】（1）；
（2）．
【解析】
【分析】（）利用加减消元法解答即可求解；
（）先化简方程组，再利用加减消元法解答即可求解；
本题考查了解一元二次方程，掌握解一元二次方程的方法是解题的关键．
【小问1详解】
解：，
得，，
∴，
把代入得，，
∴，
∴方程组的解为；
【小问2详解】
方程组整理得，，
得，，
∴，
把代入得，，
∴，
∴方程组的解为．
18. 已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x2+y2的平方根．
【答案】平方根为±10
【解析】
【分析】根据平方根、立方根的定义和已知条件可知x﹣2＝4，2x+y+7＝27，列方程解出x、y，最后代入代数式求解计算平方根即可．
【详解】解：∵x﹣2的平方根是±2，
∴x﹣2＝4，
∴x＝6，
∵2x+y+7的立方根是3
∴2x+y+7＝27
把x的值代入解得：
y＝8，
∴x2+y2=36+64=100，
它的平方根为±10．
【点睛】此题考查平方根，立方根的概念，解题关键在于掌握运算法则，难易程度适中．
19. 根据解答过程填空：
已知：如图，，，求证：．
证明：∵（邻补角的定义），
又∵（已知），
∴（____________________），
∴（____________________），
∴______，
∵（已知），
∴______，
∴（____________________），
∴（____________________）．
【答案】同角的补角相等；内错角相等，两直线平行；；；同位角相等，两直线平行；两直线平行，同位角相等．
【解析】
【分析】本题考查了平行线的判定和性质，补角的性质，由补角性质可得，进而得到，即得到，推导出，即可得，由此得到，掌握平行线的判定和性质是解题的关键．
【详解】证明：∵（邻补角的定义），
又∵（已知），
∴（同角的补角相等），
∴（内错角相等，两直线平行），
∴，
∵（已知），
∴，
∴（同位角相等，两直线平行），
∴（两直线平行，同位角相等）．
故答案为：补角性质；内错角相等，两直线平行；；；同位角相等，两直线平行；两直线平行，同位角相等．
20. 如图，直线相交于点，，平分．
（1）若，求的度数；
（2）若比大，求的度数．
【答案】（1）；
（2）．
【解析】
【分析】（）由对顶角相等可得，由垂直可得，即可得，再根据角平分线的定义可得，利用角的和差关系即可求解；
（）由可得，解方程求出，得到，再利用邻补角的定义即可求解；
本题考查了对顶角的性质，垂直的定义，角平分线的定义，一元一次方程的应用，邻补角的定义，正确识图是解题的关键．
【小问1详解】
解：∵直线相交于点，
∴，
∵，
∴，
∴，
又∵平分，
∴，
∴；
【小问2详解】
解：设，则，
∵，
∴，
解得，
∴，
∴．
21. 已知：如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DF∥CA，∠FDE＝∠A；
（1）求证：DE∥BA．
（2）若∠BFD＝∠BDF＝2∠EDC，求∠B的度数．
【答案】（1）见解析 （2）36°
【解析】
【分析】(1)根据平行线的性质与判定方法证明即可；
(2)设∠EDC=x°，由∠BFD=∠BDF = 2∠EDC可得∠BFD=∠BDF = 2x°，根据平行线的性质可得∠DFB= ∠FDE= 2x°，再根据平角的定义列方程可得x的值，进而得出∠B的度数．
小问1详解】
证明：∵DF∥CA，
∴∠DFB=∠A，
又 ∵∠FDE=∠A，
∴∠DFB=∠FDE，
∴DE∥AB；
【小问2详解】
解：设∠EDC=xº，
∵∠BFD=∠BDF=2∠EDC，
∴∠BFD=∠BDF=2xº，
由（1）可知∠DFB=∠FDE=2xº，
∴∠BDF+∠EDF+∠EDC=2xº+2xº+xº=180º，
∴x=36，
又∵DE∥AB，
∴∠B=∠EDC=36 º．
【点睛】本题主要考查了平行线的性质与判定的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
22. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具．某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计110万元；3辆A型汽车、2辆B型汽车的进价共计115万元．
（1）求A、B两种型号的汽车每辆进价分别为多少万元？
（2）若该公司计划用400万元购进以上两种型号的新能源汽车（两种型号的汽车均要购买，且400万元全部用完），问该公司有哪几种购买方案，请通过计算列举出来；
（3）若该汽车销售公司销售1辆A型汽车可获利0.8万元，销售1辆B型汽车可获利0.5万元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少万元？
【答案】（1）A型号汽车每辆进价为25万元，B型号的汽车每辆进价为20万元
（2）共有以下3种购买方案：
方案1：A型号的汽车购进4辆，B型号的汽车购进15辆；
方案2：A型号的汽车购进8辆，B型号的汽车购进10辆；
方案3：A型号的汽车购进12辆，B型号的汽车购进5辆．
（3）方案3获利最大，最大利润是12.1万元
【解析】
【分析】本题考查了二元一次方程组的应用，二元一次方程整数解，有理数混合运算的应用；
（1）等量关系式：购买2辆A型汽车的费用购买3辆B型汽车的费用110万元，购买3辆A型汽车购买2辆B型汽车的费用115万元；据此列出方程组，即可求解；
（2）设A型号的汽车购进a辆，B型号的汽车购进b辆，等量关系式：购买a辆A型号的汽车的费用购买b辆B型号的汽车的费用400万元，列出方程，求出正整数解，即可求解；
（3）根据（2）的购买方案，求出每种方案的获利情况，进行比较，即可求解；
找出等量关系式是解题的关键．
【小问1详解】
解：设A型号的汽车每辆进价为x万元，B型号的汽车每辆进价为y万元，依题意得：
，
解得：，
答：A型号的汽车每辆进价为25万元，B型号的汽车每辆进价为20万元．
【小问2详解】
解：设A型号的汽车购进a辆，B型号的汽车购进b辆，依题意得：
，
即：，
因为两种型号的汽车均购买，
所以a、b均为正整数，
所以或或，
所以共有以下3种购买方案：
方案1：A型号的汽车购进4辆，B型号的汽车购进15辆；
方案2：A型号的汽车购进8辆，B型号的汽车购进10辆；
方案3：A型号的汽车购进12辆，B型号的汽车购进5辆．
【小问3详解】
解：方案1可获利：（万元）
方案2可获利：（万元）
方案3可获利：（万元）
因为
所以方案3获利最大，最大利润是12.1万元．
23. 如图，直线，一副直角三角板，中，，，，．
（1）若按如图摆放，当平分时，则______；
（2）若，按如图摆放，求的度数；
（3）若图中固定，（如图）将绕点以每秒的速度顺时针旋转，旋转时间为秒，线段与直线首次重合时停止旋转，当线段与的一条边平行时，请求出旋转时间的值．
【答案】（1）；
（2）；
（3）或或．
【解析】
【分析】()运用角平分线定义及平行线性质即可证得结论；
()如图，过点作，利用平行线性质即可求得答案；
()设旋转时间为秒，分三种情况：当时，当时，当时，分别求出旋转角度后，列方程求解即可；
本题考查了平行线性质及判定，角平分线定义，一元一次方程应用等，正确作出辅助线是解题的关键.
【小问1详解】
解：在中，，，，
∵ 平分，
∴，
∵，
∴，
∴，
故答案为：；
【小问2详解】
解：如图，过点作，
∵，
∴，
∵，，
∴，
∴，
又∵，
∴，
∴；
【小问3详解】
解：设旋转时间为秒，由题意旋转速度为每秒转， 分三种情况：
当时，如图，此时，
∴，
∴，
解得；
当时，如图，
∴，
∴，
∴，
解得；
当时，如图，延长交于，延长交于，
∵，
∴，
∵，
∴，
∴，
∴，
解得，
综上所述，绕点顺时针旋转的时间为或或时，线段与的一条边平行．