
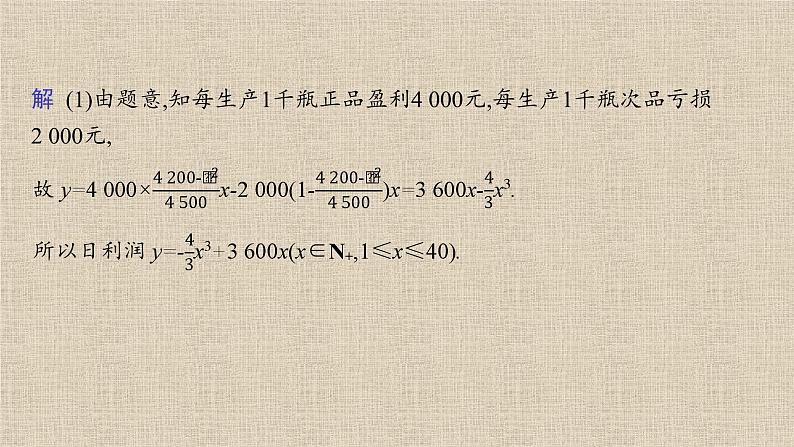






还剩20页未读,
继续阅读
2023-2024学年湘教版选择性必修第二册 习题课 导数的综合应用 课件
展开
这是一份2023-2024学年湘教版选择性必修第二册 习题课 导数的综合应用 课件,共28页。
例1某保健品企业新研发了一种健康饮品.已知每天生产该种饮品最多不超过40千瓶,最少1千瓶,经检测知生产过程中该饮品的正品率P与日产量x(x∈N+,单位:千瓶)间的关系为P= ,每生产一瓶正品盈利4元,每生产一瓶次品亏损2元.(注:正品率=饮品的正品瓶数÷饮品总瓶数×100%)(1)将日利润y(单位:元)表示成日产量x的函数;(2)求该种饮品的最大日利润.解 (1)由题意,知每生产1千瓶正品盈利4 000元,每生产1千瓶次品亏损2 000元, 则f'(x)=3 600-4x2.令f'(x)=0,解得x=30或x=-30(舍去).当1≤x<30时,f'(x)>0;当300,得x>140;令S'(x)<0,得200)在x=1处取得极值-3-c,其中a,b,c为常数.若对任意x>0,不等式f(x)≥-2c2恒成立,求c的取值范围.解 由题意知f(1)=-3-c.所以b-c=-3-c,即b=-3.对f(x)求导,得f'(x)=4ax3ln x+ax4· +4bx3=x3(4aln x+a+4b).由题意知f'(1)=0,所以a+4b=0,解得a=12.所以f'(x)=48x3ln x(x>0).令f'(x)=0,解得x=1.当01时,f'(x)>0,此时f(x)为增函数.所以f(x)在x=1处取得极小值f(1)=-3-c,并且此极小值也是最小值.所以要使f(x)≥-2c2(x>0)恒成立,只需-3-c≥-2c2即可.反思感悟(1)“恒成立”问题向最值问题转化是一种常见的题型,一般地,可采用分离参数法进行转化.λ≥f(x)恒成立⇔λ≥[f(x)]max;λ≤f(x)恒成立⇔λ≤[f(x)]min.对于不能分离参数的恒成立问题,直接求含参函数的最值即可.(2)此类问题特别要小心“最值能否取到”和“不等式中是否含等号”的情况,以此来确定参数的范围能否取得“=”.变式训练2设函数f(x)=2x3-9x2+12x+8c.(1)若对任意的x∈[0,3],都有f(x)0,f(x)单调递增;当x∈(1,2)时,f'(x)<0,f(x)单调递减;当x∈(2,3)时,f'(x)>0,f(x)单调递增.∴当x=1时,f(x)取极大值f(1)=5+8c.又f(3)=9+8c>f(1),∴x∈[0,3]时,f(x)的最大值为f(3)=9+8c.∵对任意的x∈[0,3],有f(x)9.∴c的取值范围为(-∞,-1)∪(9,+∞).(2)由(1)知f(x)0,f(x)在(0,+∞)内单调递增;②若a>0,当x∈(0,a)时,f'(x)<0,f(x)在(0,a)内单调递减,当x∈(a,+∞)时,f'(x)>0,f(x)在(a,+∞)内单调递增.综上,当a≤0时,f(x)的单调递增区间为(0,+∞),无单调递减区间;当a>0时,f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).反思感悟(1)证明f(x)>g(x)的一般方法是证明h(x)=f(x)-g(x)>0(利用单调性),特殊情况是证明f(x)min>g(x)max(最值方法),但后一种方法不具备普遍性.(2)证明二元不等式的基本思想是化为一元不等式,一种方法为变换不等式两个变元成为一个整体,另一种方法为转化后利用函数的单调性,如不等式f(x1)+g(x1)0,f(x)单调递增.当x>1时,f'(x)<0,f(x)单调递减.(2)证明 由(1)知f(x)在x=1处取得最大值,且最大值f(1)=0.所以当x≠1时,ln x0,e1-a>1,综上,当a=1时,f(x)在区间(0,e]上只有一个零点,当a<1时,f(x)在区间(0,e]上无零点.反思感悟利用导数研究函数的零点或方程根的方法是借助于导数研究函数的单调性、极值(最值),通过极值或最值的正负、函数的单调性判断函数图象走势,从而判断零点个数或者通过零点的个数求参数范围.变式训练4若函数f(x)=ax3-bx+4,当x=2时,函数f(x)取得极值- .(1)求函数f(x)的解析式;(2)若方程f(x)=k有3个不同的实数根,求实数k的取值范围.(2)由(1)可得f'(x)=x2-4=(x-2)(x+2).令f'(x)=0,得x=2或x=-2.∴当x<-2或x>2时,f'(x)>0;当-2
例1某保健品企业新研发了一种健康饮品.已知每天生产该种饮品最多不超过40千瓶,最少1千瓶,经检测知生产过程中该饮品的正品率P与日产量x(x∈N+,单位:千瓶)间的关系为P= ,每生产一瓶正品盈利4元,每生产一瓶次品亏损2元.(注:正品率=饮品的正品瓶数÷饮品总瓶数×100%)(1)将日利润y(单位:元)表示成日产量x的函数;(2)求该种饮品的最大日利润.解 (1)由题意,知每生产1千瓶正品盈利4 000元,每生产1千瓶次品亏损2 000元, 则f'(x)=3 600-4x2.令f'(x)=0,解得x=30或x=-30(舍去).当1≤x<30时,f'(x)>0;当30
相关资料
更多









