





适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练17函数与方程课件新人教A版
展开1.(2024·河北石家庄模拟)下列函数中,是奇函数且存在零点的是( )
解析 选项A,C中的函数都是奇函数,但在定义域上不存在零点,选项B中的函数存在零点但不是奇函数;对于选项D,令f(x)=y=x|x|,则f(-x)=-x|-x|=-x|x|=-f(x),所以函数是奇函数,令f(x)=x|x|=0,解得x=0,所以存在零点,故选D.
2.(2024·海南海口模拟)函数f(x)= -ln x+2的零点所在的大致区间为( )A.(1,e)B.(e,e2)C.(e2,e3)D.(e3,e4)
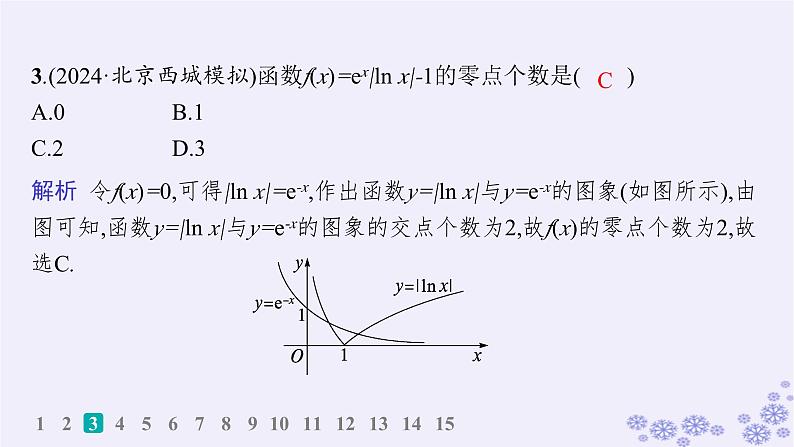
3.(2024·北京西城模拟)函数f(x)=ex|ln x|-1的零点个数是( )A.0B.1C.2D.3
解析 令f(x)=0,可得|ln x|=e-x,作出函数y=|ln x|与y=e-x的图象(如图所示),由图可知,函数y=|ln x|与y=e-x的图象的交点个数为2,故f(x)的零点个数为2,故选C.
4.(2024·北京朝阳模拟)已知函数f(x)= 若方程f(x)=1的实根在区间(k,k+1),k∈Z上,则k的最大值是( )A.-3B.-2C.1D.2
解析 当x≤-2时,f(x)=x2-5,令f(x)=1,解得x=- ;当x>-2时,f(x)=xlg(x+2),其中f(1)=lg 3<1,f(2)=2lg 4=lg 16>1,所以当f(x)=1时,可得x∈(1,2).综上,k的最大值是1,故选C.
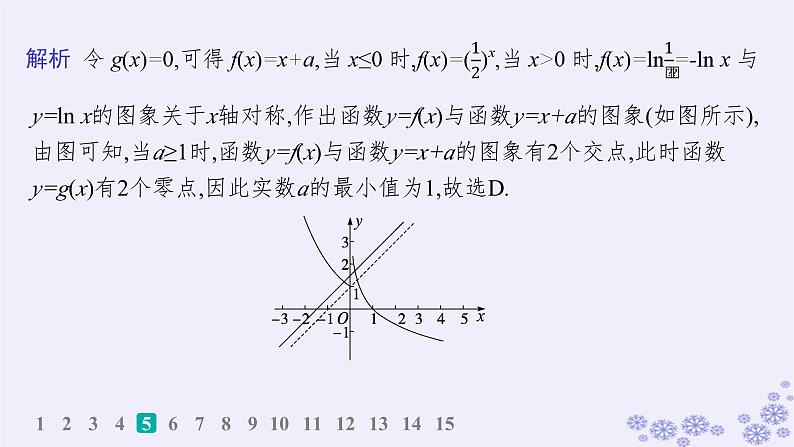
5.(2024·四川绵阳模拟)已知函数f(x)= g(x)=f(x)-x-a,若g(x)有2个零点,则实数a的最小值是( )A.2D.1
y=ln x的图象关于x轴对称,作出函数y=f(x)与函数y=x+a的图象(如图所示),由图可知,当a≥1时,函数y=f(x)与函数y=x+a的图象有2个交点,此时函数y=g(x)有2个零点,因此实数a的最小值为1,故选D.
6.(多选题)(2024·河南信阳模拟)已知函数f(x)=|1-2x|,实数a,b(a
8.(2024·山东济南模拟)函数f(x)=2sin xsin(x+ )-x2的零点个数为 .
交点的个数.在同一坐标系中分别作出两函数图象(如图所示),由图可知,函数g(x)与h(x)的图象有2个交点,所以f(x)有2个零点.
9.(2024·河北沧州模拟)若函数f(x)=x2-ax+1在区间( ,3)上有零点,则实数a的取值范围是 .
10.(2024·甘肃兰州模拟)已知x0是函数f(x)=( )x-x+4的一个零点,若x1∈(2,x0),x2∈(x0,+∞),则( )A.x0∈(2,4)B.f(x1)>f(x2)C.f(x1)<0,f(x2)<0D.f(x1)>0,f(x2)>0
解析 函数y=( )x在区间(2,+∞)上单调递减,y=-x+4在区间(2,+∞)上单调递减,故f(x)=( )x-x+4在区间(2,+∞)上单调递减,又f(2)>0,f(3)>0, f(4)>0,f(5)<0,所以x0∈(4,5),因为f(x0)=0,x1∈(2,x0),x2∈(x0,+∞),由单调性知f(x1)>0,f(x2)<0,即f(x1)>f(x2),故选B.
11.(2024·江苏南通模拟)f(x)是定义在R上的奇函数,当x∈[-1,1]时, f(x)=x,f(1+x)=f(1-x),令g(x)=f(x)-lg x,则函数g(x)的零点个数为( )A.4B.5C.6D.7
解析 由f(1+x)=f(1-x)可知f(x)的图象关于直线x=1对称,又由f(1+x)=f(1-x)可得f(2+x)=f(-x)=-f(x),所以f(4+x)=-f(2+x)=f(x),因此f(x)的周期为4.作出f(x)的图象(如图所示),g(x)=f(x)-lg x的零点个数即为f(x)的图象与y=lg x图象的交点个数,因为lg 9<1,lg 10=1,由图象可得f(x)的图象与y=lg x图象的交点个数为5,故选B.
12.(2024·湖南岳阳模拟)若函数f(x)=x2-4x+a(e2x-4+e4-2x)有唯一零点,则实数a=( )A.2B.C.4D.1
解析 由f(4-x)=(4-x)2-4(4-x)+a[e2(4-x)-4+e4-2(4-x)]=x2-4x+a(e4-2x+e2x-4)=f(x),可得函数f(x)的图象关于直线x=2对称,要使函数f(x)=x2-4x+a(e2x-4+e4-2x)有唯一的零点,则f(2)=0,即4-8+2a=0,得a=2,故选A.
13.(2024·吉林通化模拟)已知函数f(x)=|x-2|+1,g(x)=kx,若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是 .
解析 作出f(x)=|x-2|+1的图象(如图所示),直线y=kx过坐标原点O,当k≤0时,不满足方程f(x)=g(x)有两个不相等的实根,当k=1时,直线y=x与射线y=x-1 (x≥2)所在直线平行,又kOA= ,要使方程f(x)=g(x)有两个不相等的实根,由图象可知k∈( ,1).
14.(2024·辽宁沈阳模拟)若函数f(x)=x- ,则方程f2(x)-f(x)-6=0的实根个数为( )A.3B.4C.5D.6
由方程f2(x)-f(x)-6=0,得f(x)=3或f(x)=-2,结合图象,由f(x)=3,可得x有1个解;由f(x)=-2,可得x有2个解.所以方程f2(x)-f(x)-6=0的实根个数为3,故选A.
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练18函数模型及其应用课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练18函数模型及其应用课件新人教A版,共22页。
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练15对数函数课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练15对数函数课件新人教A版,共20页。PPT课件主要包含了fxlnx,4+∞等内容,欢迎下载使用。
适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练14指数函数课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第3章函数与基本初等函数课时规范练14指数函数课件新人教A版,共21页。PPT课件主要包含了ABD,x+1,ABC等内容,欢迎下载使用。












