资料中包含下列文件,点击文件名可预览资料内容





还剩3页未读,
继续阅读
成套系列资料,整套一键下载
- 第28章 锐角三角函数 单元检测卷-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版) 试卷 0 次下载
- 29 投影与视图(讲+练)【8大题型】-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版) 试卷 0 次下载
- 第29章 投影与视图 单元检测-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版) 试卷 0 次下载
- 【专项训练】解直角三角形及应用(40题)-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版) 试卷 0 次下载
- 期末数学测试卷(含反比函数)-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版) 试卷 0 次下载
综合测试卷-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版)
展开
这是一份综合测试卷-【重要笔记】2022-2023学年九年级数学下册重要考点精讲精练(人教版),文件包含综合测试卷原卷版docx、综合测试卷解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
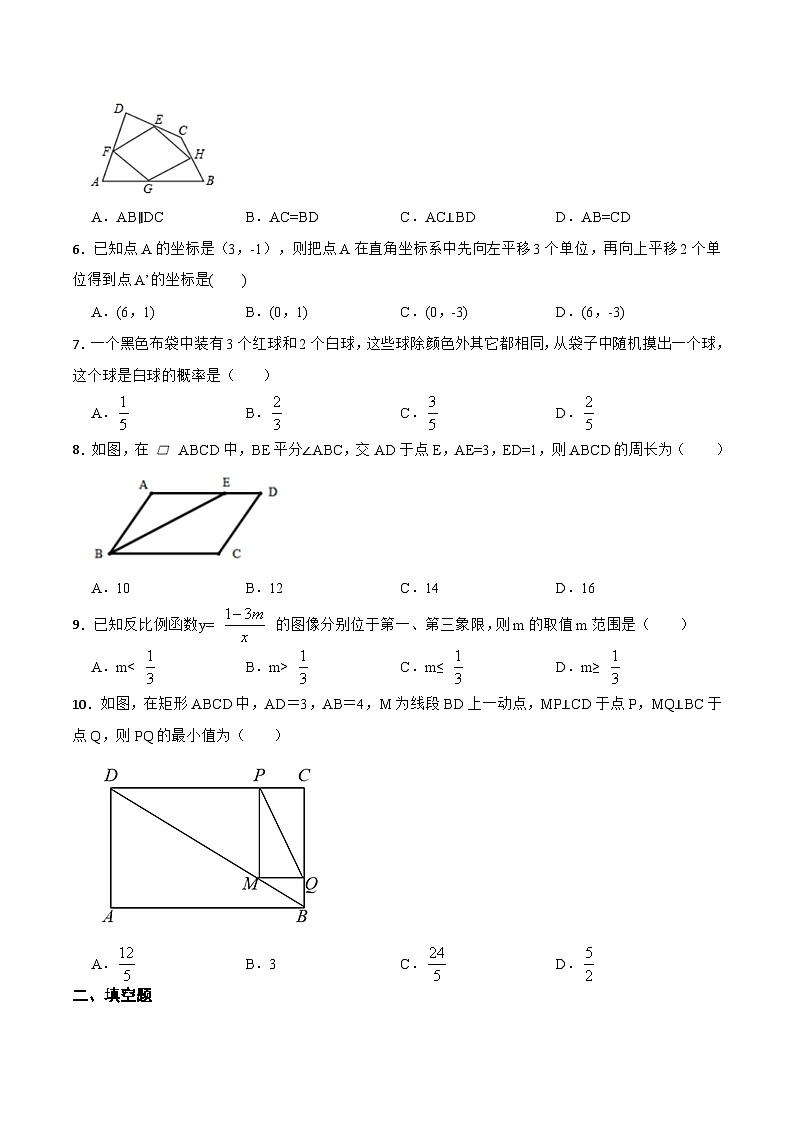
九年级综合测试卷一、单选题1.计算:|﹣ |=( )A. B. C.3 D.﹣3【答案】A【解析】【解答】解:|﹣ |= ,故选A.【分析】利用绝对值得性质可得结果.2.下列各数中,是负数的是( ) A.﹣(﹣2) B.(﹣2)2 C.|﹣2| D.﹣22【答案】D【解析】【解答】解:A、-(-2)=2>0,故A错误;B、(−2)2=4>0,故B错误;C、|-2|=2>0,故C错误;D、-22=−4<0,故D正确;故答案为:D.【分析】根据小于零的数是负数,可得答案.3.如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )A.三角形的稳定性. B.垂线段最短. C.长方形的轴对称性. D.两点之间线段最短.【答案】A【解析】【解答】解:防止变形是为了门框的稳定性,加上木条后构成了两个三角形,故依据的是三角形的稳定性.故答案为:A.【分析】考查三角形的稳定性的实践.4.如图,矩形纸片的一条边经过含有30°角的直角三角板的直角顶点,矩形纸片的一组对边与三角板的两条直角边相交形成∠1和∠2,若∠2=120°,则∠1的度数为( )A.15° B.30° C.60° D.120°【答案】B【解析】【解答】解:∵∠2+∠3=180°,∴∠3=180°−∠2.∵直尺的两边互相平行,∴∠4=∠3,∴∠4=180°−∠2.∵∠4+∠1=90°,∴180°−∠2+∠1=90°,即∠2−∠1=90°.∴∠1与∠2之间的数量关系为:∠2−∠1=90°,∵∠2=120°,∴,故答案为:B. 【分析】根据邻补角的定义可得∠3=180°−∠2,由平行线的性质可得∠4=∠3=180°−∠2,利用∠4+∠1=90°可求出∠2−∠1=90°,从而求出∠1的度数.5.如图,顺次连接四边形ABCD各边的中点的四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) A.AB∥DC B.AC=BD C.AC⊥BD D.AB=CD【答案】C【解析】【解答】依题意得:四边形EFGH是由四边形ABCD各边中点连接而成,连接AC、BD,故EF∥AC∥HG,EH∥BD∥FG,所以四边形EFGH是平行四边形,要使四边形EFGH为矩形,根据矩形的判定(有一个角为直角的平行四边形是矩形),当AC⊥BD时,∠EFG=∠EHG=90度,四边形EFGH为矩形.故答案为:C.【分析】根据矩形的判定定理(有一个角为直角的平行四边形是矩形).先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∠EFG=90度.由此推出AC⊥BD.6.已知点A的坐标是(3,-1),则把点A在直角坐标系中先向左平移3个单位,再向上平移2个单位得到点A’的坐标是( ) A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)【答案】B【解析】【解答】解:原来A点的横坐标是3,纵坐标是-1,向左平移3个单位,再向上平移2个单位得到新点A’的横坐标是3-3=0,纵坐标为-1+2=1,即为A’(0,1).故答案为:B.【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.7.一个黑色布袋中装有3个红球和2个白球,这些球除颜色外其它都相同,从袋子中随机摸出一个球,这个球是白球的概率是( ) A. B. C. D.【答案】D【解析】【解答】解:∵一个黑色布袋中装有3个红球和2个白球,这些球除颜色外其它都相同,∴抽到每个球的可能性相同,∴布袋中任意摸出1个球,共有5种可能,摸到白球可能的次数为2次,摸到白球的概率是 ,∴P(白球) .故答案为:D. 【分析】利用白球的个数除以球的总数即可求出摸到白球的概率.8.如图,在 ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则ABCD的周长为( ) A.10 B.12 C.14 D.16【答案】C【解析】【解答】解:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,AB=CD,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AB=AE=3,∵AB= 3,AD=4,∴四边形ABCD的周长=2(AD+AB)=2×7=14,故答案为:C. 【分析】平行四边形的周长等于两邻边和的2倍,只需求相邻两边长即可;根据平行线的性质与角平分线的性质,得出在三角形中等角对等边,即可计算出答案.9.已知反比例函数y= 的图像分别位于第一、第三象限,则m的取值m范围是( ) A.m< B.m> C.m≤ D.m≥ 【答案】A【解析】【解答】解:由题意,得1-3m>0,解得m< ,故答案为:A.【分析】根据反比例函数的性质,可得答案.10.如图,在矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值为( )A. B.3 C. D.【答案】A【解析】【解答】解:连接CM,如图所示:∵MP⊥CD于点P,MQ⊥BC于点Q,∴∠CPM=∠CQM=90°,∵四边形ABCD是矩形,∴BC=AD=3,CD=AB=4, ,∴∠CPM=∠CQM=∠BCD=90°,∴四边形PCQM是矩形,∴PQ=CM,∴当CM最小时,PQ最小,∵点M在BD上运动,∴当CM⊥BD时,CM最小,则PQ最小,由勾股定理得: ,∵ ,∴此时 ,∴PQ的最小值为 ,.故答案为:A.【分析】连接CM,可证四边形PCQM是矩形,得出PQ=CM,所以可知当CM最小时,PQ最小,由于点M在BD上运动,可得当CM⊥BD时,CM最小,则PQ最小,由勾股定理求出BD的长,再利用求出CM值即可.二、填空题11.已知0°<90°,当a = 时,sina =;当a = 时,tana=.【答案】30°;60°【解析】【解答】解:因为,故答案为:30°;60°.【分析】根据特殊角三角函数值进行解答即可.12.单项式的系数是 .【答案】【解析】【解答】解:由已知单项式的系数为故答案为: 【分析】根据单项式系数的定义求解即可。13.一个菱形的两条对角线长分别为3cm,4cm,这个菱形的面积S= . 【答案】6 【解析】【解答】解:菱形的面积为: 故答案为: 6 。 【分析】根据菱形的面积等于两对角线乘积的一半即可算出答案。14.如果关于 的一元二次方程 的一个解是 ,则 .【答案】2020【解析】【解答】解:把 代入方程 得: , ∴ ,∴ .故答案为:2020.【分析】由题意把x=1代入一元二次方程可得a+b的值,然后用整体代换计算可求解.15.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D是半径为2的⊙A上一动点,点M是CD的中点,则BM的最大值是 . 【答案】【解析】【解答】解:如图,取AC的中点N,连接MN,BN,∵在Rt△ABC中,∠ABC=90°,AB=4,BC=3,∵AN=NC=AC=,∴BN=AC=∵点M是CD的中点,∴DM=MC,∴MN=AD=1∴BM≤BN+NM,∴BM≤+1=,即BM的最大值是. 故答案为: 【分析】取AC的中点N,连接MN,BN,利用勾股定理求出AC的长,利用线段中点的定义可求出AN的长;再利用MN是△ADC的中位线,利用三角形的中位线定理求出MN的长;再利用三角形的三边关系定理,可得到BM≤BN+NM,代入计算可得到BM的最大值.三、解答题16.解不等式组: . 【答案】解: , 由①得:x>2,由②得:x≤3,∴不等式组的解集为2<x≤3.【解析】【分析】由题意先求得每一个不等式的解集,再根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了找出各解集的公共部分即可求解.17.先化简,再求值: ,其中 ,且x是整数. 【答案】解:原式= = = = = ,∵ ,且x是整数,∴x=1或2,又∵x≠0,2,-2,∴x=1,∴原式=4×1=4.【解析】【分析】先化简分式,再求出 x=1, 最后代入计算求解即可。18.已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.【答案】证明: 平分 , 于E 于F, , .在 和 中 , , .【解析】【分析】由垂直的概念以及角平分线的性质可得∠F=∠CEB=90°,CE=CF,证明△CEB≌△CFD,据此可得结论.四、解答题19.已知一次函数 的图象与 轴交于点 . (1)求此函数的表达式; (2)当 时,求自变量 的取值范围. 【答案】(1)解:将 代入 得 ,解得 ,所以此函数的表达式为: ;(2)解:当y>0时,即 , 解得 .【解析】【分析】(1)将A点代入,利用待定系数法即可求函数的表达式; (2)根据 ,可列出关于x的不等式,解不等式即可求出x的取值范围.20.在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:(1)图1中“统计与概率”所在扇形的圆心角为 度;(2)图2、3中的a= ,b= ;(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?【答案】(1)36(2)60;14(3)解:依题意,得45%×60=27,答:唐老师应安排27课时复习“数与代数”内容.【解析】【分析】(1)先计算出“统计与概率”所占的百分比,再乘以360即可; (2)根据数与代数所占的百分比,求得数与代数的课时总数,再减去数与式和函数,即为a的值,再用a的值减去图三中的A,B,CE的值,即为b的值; (3)用45%×60即可。21.某商场以每件20元的价格购进一种商品,经市场调查发现:该商品每天的销售量(件)与每件售价(元)之间满足一次函数关系,其图象如图所示.设该商场销售这种商品每天获利(元).(1)求与之间的函数关系式;(2)求与之间的函数关系式;(3)该商场规定这种商品每件售价不低于进价且不高于38元,商品要想获得600元的利润,每件商品的售价应定为多少元?【答案】(1)解:设与之间的函数关系式为,由所给函数图象可知∶,解得,故与的函数关系式为(2)解:,即与之间的函数关系式为(3)解:(舍)每件商品的售价应定为30元.【解析】【分析】(1)设y与x的函数关系式为y=kx+b,将(25,70)、(35,50)代入求出k、b的值,据此可得对应的函数关系式; (2)根据每天的利润=(售价-进价)×销售量可得w与x的关系式; (3)令w=600,求出x的值,由题意可得20≤x≤38,据此可得售价.五、解答题22.定义:有两边之比为的三角形叫做智慧三角形.(1)如图1,在智慧三角形中,为边上的中线,求的值; (2)如图2,是的内接三角形,为直径,过的中点作,交线段于点,交于点,连结交于点.①求证:是智慧三角形;②如图3,在(2)的条件下,当时,则=▲ .(直接写出结果)【答案】(1)解: 是 的中线, , , , , , ;(2)解:①如图,连结 ,设 , , , , , , , , , , , , 是 的中点, , , ,即 , 是智慧三角形;②【解析】【解答】(2)②如图,过点 作 交 于点 , , , , ,设 ,则 ,由①可得, , , , , , ,∴ ,故答案为: .【分析】(1)利用线段中点的定义可求出BD的长,可得到,利用有两边对应成比例且夹角相等,可证得△ABD∽△CBA,利用相似三角形的对应边成比例,可求出的值.(2)①连接OE,设∠ABE=α,利用圆周角定理可表示出∠AOE,利用等边对等角及三角形的内角和定理可表示出∠OAE,再证明∠AED=∠ABE,利用有两组对应角分别相等的两三角形相似,可证得△ADE∽△AEB,利用相似三角形的对应边成比例,可证得AE2=AD·AB,利用线段中点的定义,可推出,由此可证得结论;②过点G作GI∥AB交DE于点I,可证得△FGI∽△FAD∽△EIG∽△EDB,利用相似三角形的对应边成比例可得到EG和BE的比值,设EG=3a,BE=5a;由△ADE∽△AEB,利用相似三角形的对应边成比例,可表示出DE,EI,DI及IF的长,根据EF=EI+IF,可表示出EF的长;然后代入求出EG与EF的比值.23.如图,动点P在函数y(x>0)的图象上,过点P分别作x轴和y轴的平行线,交函数y的图象于点A、B,连接AB、OA、OB.设点P横坐标为a.(1)直接写出点P、A、B的坐标(用a的代数式表示);(2)点P在运动的过程中,△AOB的面积是否为定值?若是,求出此定值;若不是,请说明理由;(3)在平面内有一点Q (,1),且点Q始终在△PAB的内部(不包含边),求a的取值范围.【答案】(1)解:P(a,),A(,),B(a,);(2)解:是定值.理由如下:∵,∴.∴△AOB的面积是定值.(3)解:设直线AB的解析式为,把A(,),B(a,)代入,得:,解得:,∴直线AB的解析式为,当时,,∵点Q始终在△PAB的内部(不包含边),∴,且,且,解得:且,综上所述,a的取值范围是且.【解析】【解答】解:(1)∵点P在函数y(x>0)的图象上,点P横坐标为a,∴P(a,),∵PA//x轴,PB//y轴,∴A(,),B(a,);【分析】(1)根据函数解析式,PA//x轴,PB//y轴,求解即可; (2)先求出PA和PB,再利用三角形的面积公式计算求解即可; (3)利用待定系数法求函数解析式即可。
九年级综合测试卷一、单选题1.计算:|﹣ |=( )A. B. C.3 D.﹣3【答案】A【解析】【解答】解:|﹣ |= ,故选A.【分析】利用绝对值得性质可得结果.2.下列各数中,是负数的是( ) A.﹣(﹣2) B.(﹣2)2 C.|﹣2| D.﹣22【答案】D【解析】【解答】解:A、-(-2)=2>0,故A错误;B、(−2)2=4>0,故B错误;C、|-2|=2>0,故C错误;D、-22=−4<0,故D正确;故答案为:D.【分析】根据小于零的数是负数,可得答案.3.如图,木工师傅在做完门框后,为防止变形经常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的依据是( )A.三角形的稳定性. B.垂线段最短. C.长方形的轴对称性. D.两点之间线段最短.【答案】A【解析】【解答】解:防止变形是为了门框的稳定性,加上木条后构成了两个三角形,故依据的是三角形的稳定性.故答案为:A.【分析】考查三角形的稳定性的实践.4.如图,矩形纸片的一条边经过含有30°角的直角三角板的直角顶点,矩形纸片的一组对边与三角板的两条直角边相交形成∠1和∠2,若∠2=120°,则∠1的度数为( )A.15° B.30° C.60° D.120°【答案】B【解析】【解答】解:∵∠2+∠3=180°,∴∠3=180°−∠2.∵直尺的两边互相平行,∴∠4=∠3,∴∠4=180°−∠2.∵∠4+∠1=90°,∴180°−∠2+∠1=90°,即∠2−∠1=90°.∴∠1与∠2之间的数量关系为:∠2−∠1=90°,∵∠2=120°,∴,故答案为:B. 【分析】根据邻补角的定义可得∠3=180°−∠2,由平行线的性质可得∠4=∠3=180°−∠2,利用∠4+∠1=90°可求出∠2−∠1=90°,从而求出∠1的度数.5.如图,顺次连接四边形ABCD各边的中点的四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) A.AB∥DC B.AC=BD C.AC⊥BD D.AB=CD【答案】C【解析】【解答】依题意得:四边形EFGH是由四边形ABCD各边中点连接而成,连接AC、BD,故EF∥AC∥HG,EH∥BD∥FG,所以四边形EFGH是平行四边形,要使四边形EFGH为矩形,根据矩形的判定(有一个角为直角的平行四边形是矩形),当AC⊥BD时,∠EFG=∠EHG=90度,四边形EFGH为矩形.故答案为:C.【分析】根据矩形的判定定理(有一个角为直角的平行四边形是矩形).先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∠EFG=90度.由此推出AC⊥BD.6.已知点A的坐标是(3,-1),则把点A在直角坐标系中先向左平移3个单位,再向上平移2个单位得到点A’的坐标是( ) A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)【答案】B【解析】【解答】解:原来A点的横坐标是3,纵坐标是-1,向左平移3个单位,再向上平移2个单位得到新点A’的横坐标是3-3=0,纵坐标为-1+2=1,即为A’(0,1).故答案为:B.【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.7.一个黑色布袋中装有3个红球和2个白球,这些球除颜色外其它都相同,从袋子中随机摸出一个球,这个球是白球的概率是( ) A. B. C. D.【答案】D【解析】【解答】解:∵一个黑色布袋中装有3个红球和2个白球,这些球除颜色外其它都相同,∴抽到每个球的可能性相同,∴布袋中任意摸出1个球,共有5种可能,摸到白球可能的次数为2次,摸到白球的概率是 ,∴P(白球) .故答案为:D. 【分析】利用白球的个数除以球的总数即可求出摸到白球的概率.8.如图,在 ABCD中,BE平分∠ABC,交AD于点E,AE=3,ED=1,则ABCD的周长为( ) A.10 B.12 C.14 D.16【答案】C【解析】【解答】解:∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,AB=CD,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AB=AE=3,∵AB= 3,AD=4,∴四边形ABCD的周长=2(AD+AB)=2×7=14,故答案为:C. 【分析】平行四边形的周长等于两邻边和的2倍,只需求相邻两边长即可;根据平行线的性质与角平分线的性质,得出在三角形中等角对等边,即可计算出答案.9.已知反比例函数y= 的图像分别位于第一、第三象限,则m的取值m范围是( ) A.m< B.m> C.m≤ D.m≥ 【答案】A【解析】【解答】解:由题意,得1-3m>0,解得m< ,故答案为:A.【分析】根据反比例函数的性质,可得答案.10.如图,在矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值为( )A. B.3 C. D.【答案】A【解析】【解答】解:连接CM,如图所示:∵MP⊥CD于点P,MQ⊥BC于点Q,∴∠CPM=∠CQM=90°,∵四边形ABCD是矩形,∴BC=AD=3,CD=AB=4, ,∴∠CPM=∠CQM=∠BCD=90°,∴四边形PCQM是矩形,∴PQ=CM,∴当CM最小时,PQ最小,∵点M在BD上运动,∴当CM⊥BD时,CM最小,则PQ最小,由勾股定理得: ,∵ ,∴此时 ,∴PQ的最小值为 ,.故答案为:A.【分析】连接CM,可证四边形PCQM是矩形,得出PQ=CM,所以可知当CM最小时,PQ最小,由于点M在BD上运动,可得当CM⊥BD时,CM最小,则PQ最小,由勾股定理求出BD的长,再利用求出CM值即可.二、填空题11.已知0°<90°,当a = 时,sina =;当a = 时,tana=.【答案】30°;60°【解析】【解答】解:因为,故答案为:30°;60°.【分析】根据特殊角三角函数值进行解答即可.12.单项式的系数是 .【答案】【解析】【解答】解:由已知单项式的系数为故答案为: 【分析】根据单项式系数的定义求解即可。13.一个菱形的两条对角线长分别为3cm,4cm,这个菱形的面积S= . 【答案】6 【解析】【解答】解:菱形的面积为: 故答案为: 6 。 【分析】根据菱形的面积等于两对角线乘积的一半即可算出答案。14.如果关于 的一元二次方程 的一个解是 ,则 .【答案】2020【解析】【解答】解:把 代入方程 得: , ∴ ,∴ .故答案为:2020.【分析】由题意把x=1代入一元二次方程可得a+b的值,然后用整体代换计算可求解.15.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D是半径为2的⊙A上一动点,点M是CD的中点,则BM的最大值是 . 【答案】【解析】【解答】解:如图,取AC的中点N,连接MN,BN,∵在Rt△ABC中,∠ABC=90°,AB=4,BC=3,∵AN=NC=AC=,∴BN=AC=∵点M是CD的中点,∴DM=MC,∴MN=AD=1∴BM≤BN+NM,∴BM≤+1=,即BM的最大值是. 故答案为: 【分析】取AC的中点N,连接MN,BN,利用勾股定理求出AC的长,利用线段中点的定义可求出AN的长;再利用MN是△ADC的中位线,利用三角形的中位线定理求出MN的长;再利用三角形的三边关系定理,可得到BM≤BN+NM,代入计算可得到BM的最大值.三、解答题16.解不等式组: . 【答案】解: , 由①得:x>2,由②得:x≤3,∴不等式组的解集为2<x≤3.【解析】【分析】由题意先求得每一个不等式的解集,再根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了找出各解集的公共部分即可求解.17.先化简,再求值: ,其中 ,且x是整数. 【答案】解:原式= = = = = ,∵ ,且x是整数,∴x=1或2,又∵x≠0,2,-2,∴x=1,∴原式=4×1=4.【解析】【分析】先化简分式,再求出 x=1, 最后代入计算求解即可。18.已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.【答案】证明: 平分 , 于E 于F, , .在 和 中 , , .【解析】【分析】由垂直的概念以及角平分线的性质可得∠F=∠CEB=90°,CE=CF,证明△CEB≌△CFD,据此可得结论.四、解答题19.已知一次函数 的图象与 轴交于点 . (1)求此函数的表达式; (2)当 时,求自变量 的取值范围. 【答案】(1)解:将 代入 得 ,解得 ,所以此函数的表达式为: ;(2)解:当y>0时,即 , 解得 .【解析】【分析】(1)将A点代入,利用待定系数法即可求函数的表达式; (2)根据 ,可列出关于x的不等式,解不等式即可求出x的取值范围.20.在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:(1)图1中“统计与概率”所在扇形的圆心角为 度;(2)图2、3中的a= ,b= ;(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?【答案】(1)36(2)60;14(3)解:依题意,得45%×60=27,答:唐老师应安排27课时复习“数与代数”内容.【解析】【分析】(1)先计算出“统计与概率”所占的百分比,再乘以360即可; (2)根据数与代数所占的百分比,求得数与代数的课时总数,再减去数与式和函数,即为a的值,再用a的值减去图三中的A,B,CE的值,即为b的值; (3)用45%×60即可。21.某商场以每件20元的价格购进一种商品,经市场调查发现:该商品每天的销售量(件)与每件售价(元)之间满足一次函数关系,其图象如图所示.设该商场销售这种商品每天获利(元).(1)求与之间的函数关系式;(2)求与之间的函数关系式;(3)该商场规定这种商品每件售价不低于进价且不高于38元,商品要想获得600元的利润,每件商品的售价应定为多少元?【答案】(1)解:设与之间的函数关系式为,由所给函数图象可知∶,解得,故与的函数关系式为(2)解:,即与之间的函数关系式为(3)解:(舍)每件商品的售价应定为30元.【解析】【分析】(1)设y与x的函数关系式为y=kx+b,将(25,70)、(35,50)代入求出k、b的值,据此可得对应的函数关系式; (2)根据每天的利润=(售价-进价)×销售量可得w与x的关系式; (3)令w=600,求出x的值,由题意可得20≤x≤38,据此可得售价.五、解答题22.定义:有两边之比为的三角形叫做智慧三角形.(1)如图1,在智慧三角形中,为边上的中线,求的值; (2)如图2,是的内接三角形,为直径,过的中点作,交线段于点,交于点,连结交于点.①求证:是智慧三角形;②如图3,在(2)的条件下,当时,则=▲ .(直接写出结果)【答案】(1)解: 是 的中线, , , , , , ;(2)解:①如图,连结 ,设 , , , , , , , , , , , , 是 的中点, , , ,即 , 是智慧三角形;②【解析】【解答】(2)②如图,过点 作 交 于点 , , , , ,设 ,则 ,由①可得, , , , , , ,∴ ,故答案为: .【分析】(1)利用线段中点的定义可求出BD的长,可得到,利用有两边对应成比例且夹角相等,可证得△ABD∽△CBA,利用相似三角形的对应边成比例,可求出的值.(2)①连接OE,设∠ABE=α,利用圆周角定理可表示出∠AOE,利用等边对等角及三角形的内角和定理可表示出∠OAE,再证明∠AED=∠ABE,利用有两组对应角分别相等的两三角形相似,可证得△ADE∽△AEB,利用相似三角形的对应边成比例,可证得AE2=AD·AB,利用线段中点的定义,可推出,由此可证得结论;②过点G作GI∥AB交DE于点I,可证得△FGI∽△FAD∽△EIG∽△EDB,利用相似三角形的对应边成比例可得到EG和BE的比值,设EG=3a,BE=5a;由△ADE∽△AEB,利用相似三角形的对应边成比例,可表示出DE,EI,DI及IF的长,根据EF=EI+IF,可表示出EF的长;然后代入求出EG与EF的比值.23.如图,动点P在函数y(x>0)的图象上,过点P分别作x轴和y轴的平行线,交函数y的图象于点A、B,连接AB、OA、OB.设点P横坐标为a.(1)直接写出点P、A、B的坐标(用a的代数式表示);(2)点P在运动的过程中,△AOB的面积是否为定值?若是,求出此定值;若不是,请说明理由;(3)在平面内有一点Q (,1),且点Q始终在△PAB的内部(不包含边),求a的取值范围.【答案】(1)解:P(a,),A(,),B(a,);(2)解:是定值.理由如下:∵,∴.∴△AOB的面积是定值.(3)解:设直线AB的解析式为,把A(,),B(a,)代入,得:,解得:,∴直线AB的解析式为,当时,,∵点Q始终在△PAB的内部(不包含边),∴,且,且,解得:且,综上所述,a的取值范围是且.【解析】【解答】解:(1)∵点P在函数y(x>0)的图象上,点P横坐标为a,∴P(a,),∵PA//x轴,PB//y轴,∴A(,),B(a,);【分析】(1)根据函数解析式,PA//x轴,PB//y轴,求解即可; (2)先求出PA和PB,再利用三角形的面积公式计算求解即可; (3)利用待定系数法求函数解析式即可。
相关资料
更多









