2023-2024学年安徽省安庆市潜山市七年级（上）期末数学试卷（含解析）

这是一份2023-2024学年安徽省安庆市潜山市七年级（上）期末数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列四个数中，绝对值最大的是( )
A. −1B. −112C. 0D. 2
2.下列6个代数式：a+1，−3ab7，5π，−2a+5b，a，1a，其中单项式有( )
A. 1个B. 2个C. 3个D. 4个
3.第十九届亚运会在美丽的杭州举行，门票收入约6.1亿元(610000000元)，6.1亿用科学记数法表示为( )
A. 61×108B. 6.1×108C. 6.1×109D. 61×109
4.为了调查某校学生中午是否在校就餐情况，在全校的2400名学生中随机抽取了100名学生，下列说法正确的是( )
A. 此次调查属于全面调查B. 2400名学生是总体
C. 样本容量是100D. 被抽取的每一名学生称为个体
5.若2a2+b=4，则代数式3−4a2−2b的值为( )
A. 11B. 7C. −1D. −5
6.关于x、y的方程组ax+3y=92x−y=1无解，则a的值为( )
A. −6B. 6C. 9D. 30
7.已知线段AB=6cm，在直线AB上取一点C，使BC=2cm，则线段AB的中点M与AC的中点N的距离为( )
A. 1cmB. 3cmC. 2cm或3cmD. 1cm或3cm
8.某校七年级学生计划乘客车去春游，如果减少一辆客车，每辆车正好坐60人．如果增加一辆客车，每辆正好坐45人，则七年级共有学生
( )
A. 240人B. 300人C. 360人D. 420人
9.若∠1与∠2互为余角，∠1与∠3互为补角，则下列结论：
①∠3−∠2=90°；②∠3+∠2=270°−2∠1；③∠3−∠1=2∠2；④∠3<∠1+∠2.其中正确的是( )
A. ①B. ①②C. ①②③D. ①②③④
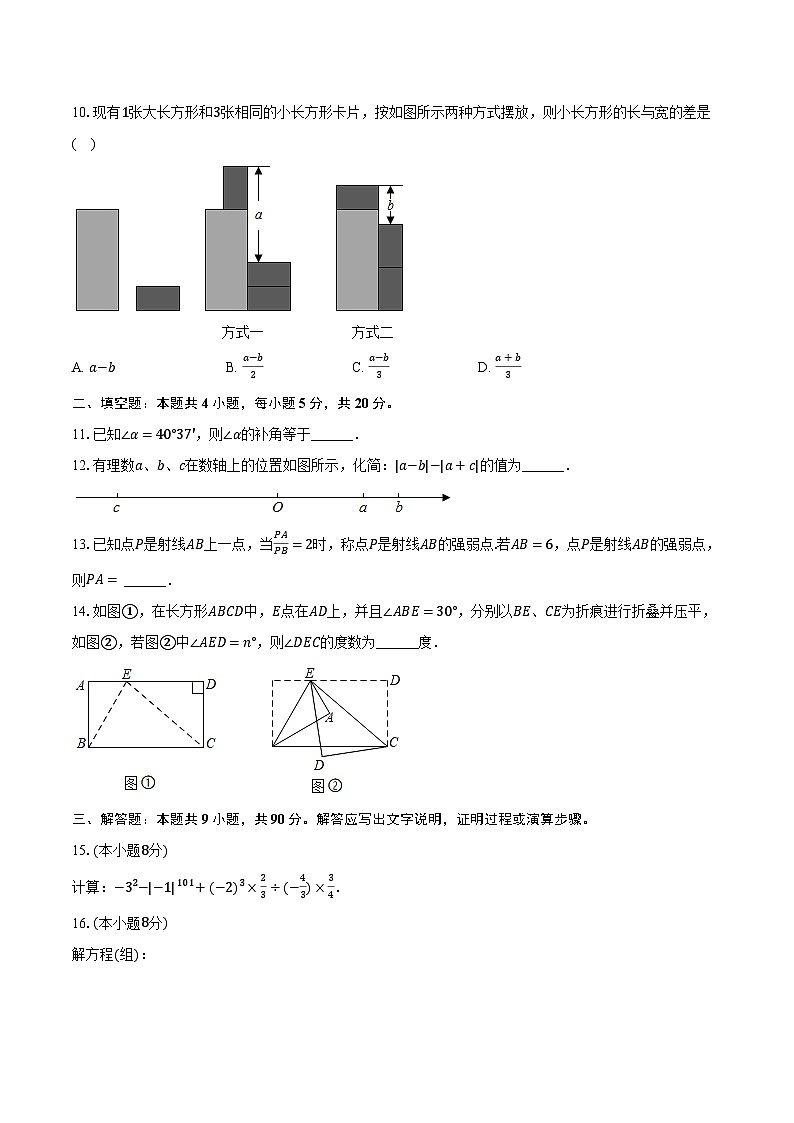
10.现有1张大长方形和3张相同的小长方形卡片，按如图所示两种方式摆放，则小长方形的长与宽的差是( )
A. a−bB. a−b2C. a−b3D. a+b3
二、填空题：本题共4小题，每小题5分，共20分。
11.已知∠α=40°37′，则∠α的补角等于______．
12.有理数a、b、c在数轴上的位置如图所示，化简：|a−b|−|a+c|的值为______．
13.已知点P是射线AB上一点，当PAPB=2时，称点P是射线AB的强弱点.若AB=6，点P是射线AB的强弱点，则PA= ______．
14.如图①，在长方形ABCD中，E点在AD上，并且∠ABE=30°，分别以BE、CE为折痕进行折叠并压平，如图②，若图②中∠AED=n°，则∠DEC的度数为______度．
三、解答题：本题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
计算：−32−|−1|101+(−2)3×23÷(−43)×34．
16.(本小题8分)
解方程(组)：
(1)3x−12−1=0.4x−10.3；
(2)2m−n=3m+2n=−1．
17.(本小题8分)
化简并求值：2(a2b−ab2)−3(ab2+a2b−1)+5ab2−5，其中实数a、b满足|a+1|+(b−3)2=0．
18.(本小题8分)
对有理数x、y，定义新运算x⊗y=ax+by+5，其中a，b为常数，已知1⊗2=10，(−2)⊗2=7．
(1)求a，b的值；
(2)如果x=−3，x⊗y=−18，求y的值．
19.(本小题10分)
数学家欧拉最先把关于x的多项式用记号f(x)来表示．例如：f(x)=x2+x−1，当x=a时．多项式的值用f(a)来表示，即f(a)=a2+a−1.当x=3时，f(3)=32+3−1=11．
(1)已知f(x)=x2−2x+3，求f(1)的值．
(2)已知f(x)=mx2−2x−m，当f(−3)=m−1时，求m的值．
(3)已知f(x)=kx2−ax−bk(a.b为常数)，对于任意有理数k，总有f(−2)=−2，求a，b的值．
20.(本小题10分)
已知：线段AB=60cm．
(1)如图1，点P沿线段AB自点A向点B以2cm/s运动，同时点Q沿线段BA自点B向点A以3cm/s运动，求几秒钟后，P、Q两点第一次相距15cm？
(2)如图2，AO=PO=10cm，∠POB=40°，点P绕点O以10度/秒的速度顺时针旋转一周停止，同时点Q沿直线BA自点B向点A运动，假如P、Q两点能相遇，求点Q运动的速度．
21.(本小题12分)
为了解某校七年级学生对《少年中国强》(A)、《开门大吉》(B)、《远方的家》(C)、《星光大道》(D)四个电视节目的喜爱情况，某调查组从该校七年级学生中随机抽取了m位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目)，并将调查结果绘制成如下两幅不完整的统计图(图1，图2)．
根据以上信息，回答下列问题：
(1)m= ______，n= ______；
(2)在图1中，喜爱《开门大吉》(B)节目所对应的扇形的圆心角的度数是______；
(3)请根据以上信息补全图2的条形统计图；
(4)已知该校七年级共有800名学生，那么他们当中最喜欢《远方的家》(C)这个节目的学生有多少人？
22.(本小题12分)
潜山市某商场经销的A、B两种商品，A种商品每件售价为60元，利润率为50%；B种商品每件进价为50元，售价为80元．
(1)A种商品每件进价为______元，每件B种商品利润率为______．
(2)若该商场同时购进A、B两种商品共70件，售完之后恰好总利润为1580元，求购进A种商品多少件？
(3)在“春节”期间，该商场只对A、B两种商品进行如下的优惠促销活动：
按上述优惠条件，若小明一次性购买商品A、B优惠后付款总额为531元，若没有优惠促销，小明在该商场购买同样商品要付多少元？
23.(本小题14分)
如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB、∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的奇妙线．
(1)一个角的角平分线______这个角的奇妙线．(填是或不是)
(2)如图2，若∠MPN=60°，射线PQ绕点P从PN位置开始，以每秒10°的速度逆时针旋转，当∠QPN首次等于180°时停止旋转，设旋转的时间为t(s)．
①当t为何值时，射线PM是∠QPN的奇妙线？
②若射线PM同时绕点P以每秒6°的速度逆时针旋转，并与PQ同时停止旋转．请求出当射线PQ是∠MPN的奇妙线时t的值．
答案和解析
1.【答案】D
【解析】解：∵−1、−112、0、−2的绝对值分别为1、112、0、2，
2>112>1>0，
∴绝对值最大的是2．
故选：D．
先求出每个数的绝对值，再根据实数的大小比较法则比较即可．
本题考查了有理数大小比较以及绝对值，掌握有理数大小比较方法是解答本题的关键．
2.【答案】C
【解析】解：单项式有：−3ab7，5π，a，共3个，
故选：C．
数字与字母的积叫做单项式，单独的一个数或字母也是单项式，由此判断即可．
本题考查了单项式，熟知单项式的定义是解题的关键．
3.【答案】B
【解析】解：6.1亿=610000000=6.1×108．
故选：B．
科学记数法的表现形式为a×10n的形式，其中1≤|a|<10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数；由此进行求解即可得到答案．
本题主要考查了科学记数法的表示方法，熟练掌握科学记数法的表示方法是解题的关键．
4.【答案】C
【解析】解：A、此次调查属于抽样调查，故此选项不符合题意；
B、2400名学生的在校就餐情况是总体，故此选项不符合题意；
C、样本容量是100，故此选项符合题意；
D、被抽取的每一名学生的在校就餐情况为个体，故此选项不符合题意．
故选：C．
总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体．
此题主要考查了总体、个体、样本．正确理解总体、个体、样本的概念是解决本题的关键．
5.【答案】D
【解析】解：∵2a2+b=4，
则原式=3−2(2a2+b)
=3−8
=−5．
故选：D．
原式后两项提取−2变形，再将已知代数式的值变形后代入计算即可求出值．
此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．
6.【答案】A
【解析】解：原方程组ax+3y=9(1)2x−y=1(2)，由(2)式得y=2x−1，代入(1)式得：
ax+6x−3=9，
解得x=12a+6，当a+6=0时原方程组无解，a=−6．
故选：A．
由第二个方程可得y=2x−1，将此式代入第一个方程可以得到一个关于x解的方程，当分母为零时原方程组无解，即可得a的值．
本题考查了二元一次方程组的解，解答此题的关键是熟知方程组无解的含义．
7.【答案】A
【解析】解：①当C在线段AB上时，
因为AB=6cm，M是AB的中点，
所以AM=12AB=12×6=3cm，
又因为BC=2cm，
所以AC=AB−BC=6−2=4cm，
因为N是线段AC的中点，
所以AN=12AC=12×4=2cm，
所以MN=AM−AN=3−2=1cm；
②当C在线段AB的延长线上时，
因为AB=6cm，M是AB的中点，
所以AM=12AB=12×6=3cm，
又因为BC=2cm，
所以AC=AB+BC=6+2=8cm，
因为N是线段AC的中点，
所以AN=12AC=12×8=4cm，
所以MN=AN−AM=4−3=1cm，
综上：MN=1cm．
故选：A．
根据题意画出符合条件的两种情况，求出AC的值，根据线段中点定义得出AM=12AB，AN=12AC，根据MN=AM−AN或MN=AN−AM计算可得．
本题考查了求两点间的距离和线段中点的定义，主要考查学生的计算能力，关键是分类讨论．
8.【答案】C
【解析】【分析】
此题考查一元一次方程的实际运用，解题关键是要读懂题目的意思，根据题目给出的条件，找到关键描述语，找出合适的等量关系，列出方程，再求解.学生数为未知量，每辆车的载重学生数是已知的，应根据等量关系：每辆车坐60人所需车辆数+1=每辆车坐45人所需车辆数−1列方程解答即可．
【解答】
解：设七年级共有x名学生
则根据题意有：x60+1=x45−1，
解得x=360，
答：七年级共有360名学生．
故选C．
9.【答案】C
【解析】解：根据题意得：(1)∠1+∠2=90°，(2)∠1+∠3=180°，
则(2)−(1)得，∠3−∠2=90°，
①正确；
(1)+(2)得，∠1+∠2+∠1+∠3=270°，
则∠3+∠2=270°−2∠1，
②正确；
(2)−(1)×2得，∠3−∠1=2∠2，
③正确；
因为(1)∠1+∠2=90°，(2)∠1+∠3=180°，
所以2(∠1+∠2)=180°，
所以∠3=180°−∠1
=2(∠1+∠2)−∠1
=∠1+2∠2，
所以∠3>∠1+∠2，
④错误；
故选：C．
根据题意得：①(1)∠1+∠2=90°，(2)∠1+∠3=180°，(2)−(1)得出结果进行判断；
②(1)+(2)得出结果进行判断；
③(2)−(1)×2得出结果进行判断；
④先把(1)等式两边乘2得2(∠1+∠2)=180°，把(2)变形后代入2(∠1+∠2)=180°，得出结果进行判断．
本题考查余角和补角，掌握余角和补角的定义，根据题目的要求对两个等式进行不同的计算是解题关键．
10.【答案】C
【解析】解：设小长方形的长为x、宽为y，大长方形的长为m，
则a+2y=x+m，2x+b=y+m，
∴x=a+2y−m，y=2x+b−m，
∴x−y=(a+2y−m)−(2x+b−m)，
即x−y=a+2y−m−2x−b+m，
3x−3y=a−b，
∴x−y=a−b3，
即小长方形的长与宽的差是a−b3，
故选：C．
设小长方形的长为x、宽为y，大长方形的长为m，结合图形得出a+2y=x+m，2x+b=y+m，据此知x=a+2y−m，y=2x+b−m，继而得x−y=(a+2y−m)−(2x+b−m)，整理可知3x−3y=a−b，据此可得答案．
本题主要考查整式的加减，整式的加减的实质就是去括号、合并同类项．一般步骤是：先去括号，然后合并同类项．
11.【答案】139°23′
【解析】解：∵∠α=40°37′，
∴∠α的补角为：180°−∠α=139°23′．
故答案为：139°23′．
由补角的定义进行求解即可．
本题主要考查补角，解答的关键是明确互补的两角之和为180°．
12.【答案】b+c
【解析】解：根据数轴上点的位置得：c<0则a−b<0，a+c<0，
则原式=−(a−b)+(a+c)=−a+b+a+c=b+c．
故答案为：b+c．
根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，计算即可得到结果．
本题考查数轴、绝对值等知识，解题的关键是记住绝对值的性质：数a绝对值要由字母a本身的取值来确定：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数−a；③当a是零时，a的绝对值是零．
13.【答案】4或12
【解析】解：①点P在线段AB上时，
，
∵PAPB=2，AB=6，
∴PA=4，
②点P在线段AB的延长线上时，
，
∵PAPB=2，AB=6，
∴PA=12，
故答案为：4或12．
分点P在线段AB上、点P在线段AB的延长线上两种情况讨论．
本题考查了两点间的距离，关键是注意分类讨论．
14.【答案】(30+n2)
【解析】解：折叠后的图形如下：
∵∠ABE=30°，
∴∠BEA′=∠BEA=60°，
又∵∠CED′=∠CED，
∴∠DEC=12∠DED′，
∴∠DEC=12(180°−∠A′EA+∠AED)
=12(180°−120°+n°)
=(30+12n)°
故答案为：(30+12n)．
求∠CED的大小只需根据折叠规律、平角知识和角的和差求出∠CED大小即可．
本题综合考查了角的计算、图形的折叠特性，同时也可以用平角建立等量关系，方程的思想求解更简单．
15.【答案】解：−32−|−1|101+(−2)3×23÷(−43)×34
=−9−1+(−8)×23×(−34)×34
=−9−1+3
=−7．
【解析】先算乘方，再算乘除法，最后算加减法即可．
本题考查有理数的混合运算，熟练掌握运算法则是解答本题的关键．
16.【答案】解：(1)原方程可化为3x−12−1=4x−103，
去分母得：3(3x−1)−6=2(4x−10)，
去括号得，9x−3−6=8x−20，
移项得，9x−8x=−20+3+6，
合并同类项得：x=−11；
(2)2m−n=3①m+2n=−1②，
①×2+②得：5m=5，
解得：m=1，
把m=1代入②得：n=−1，
则方程组的解为m=1n=−1．
【解析】(1)先把方程的分母化为整数，再去分母，去括号，移项合并同类项即可；
(2)先利用加减消元法求出m的值，再利用代入消元法求出n的值即可．
此题考查了解二元一次方程组及解一元一次方程，熟练掌握运算法则是解本题的关键．
17.【答案】解：原式=2a2b−2ab2−3ab2−3a2b+3+5ab2−5
=−a2b−2；
∵|a+1|+(b−3)2=0，
∴a+1=0，b−3=0，
∴a=−1，b=3，
原式=−(−1)2×3−2=−1×3−2=−5．
【解析】将原式去括号，合并同类项，根据绝对值及偶次幂的非负性求得a，b的值后代入化简结果中计算即可．
本题考查整式的化简求值，绝对值及偶次幂的非负性，熟练掌握相关运算法则是解题的关键．
18.【答案】解：(1)由题意得a+2b+5=10−2a+2b+5=7，
解得a=1b=2；
(2)由(1)知，a=1，b=2，
∵x⊗y=ax+by+5，
∴x⊗y=x+2y+5，
∵x⊗y=−18，
∴x+2y+5=−18，
∵x=−3，
∴−3+2y+5=−18，
解得y=−10．
【解析】(1)根据题意得出关于a、b的方程组，求出ab的值即可；
(2)根据x=−3，x⊗y=−18得出关于y的方程，求出y的值即可．
此题考查了解二元一次方程组，有理数的混合运算及二元一次方程的解，根据题意得出关于ab的方程组是解题的关键．
19.【答案】解：(1)当x=1时，f(1)=1−2+3=2；
(2)当x=−3时，f(−3)=mx2−2x−m=9m+6−m=m−1，
∴m=−1；
(3)当x=−2时，f(−2)=kx2−ax−bk=4k+2a−bk=−2，
∴(4−b)k+2a=−2，
∵k为任意有理数，
∴4−b=0，2a=−2，
∴a=−1，b=4．
【解析】(1)将x=1代入f(x)=x2−2x+3中进行计算即可；
(2)将x=−3代入f(x)=mx2−2x−m中，根据f(−3)=m−1列方程计算即可；
(3)根据题意将x=−2代入f(x)=kx2−ax−bk中，可知k的倍数4−b=0，从而可解答此题．
本题主要考查的是求代数式的值，读懂记号f(x)的运算方法是解题的关键．
20.【答案】解：(1)设x秒钟后，P，Q两点第一次相距15cm，
根据题意得：2x+3x+15=60，
解得：x=9．
答：9秒钟后，P，Q两点第一次相距15cm；
(2)点P，Q只能在直线AB上相遇，
点P旋转到直线AB上的时间为40÷10=4(秒)或(40+180)÷10=22(秒)．
设点Q运动的速度y cm/s，
根据题意得：4y=60−10×2或22y=60，
解得：y=10或y=3011．
答：点Q运动的速度为10cm/s或3011cm/s．
【解析】(1)设x秒钟后，P，Q两点第一次相距15cm，利用路程=速度×时间，结合P，Q两点第一次相距15cm，可列出关于x的一元一次方程，解之即可得出结论；
(2)由点P，Q的运动规律，可得出点P，Q只能在直线AB上相遇，利用旋转时间=度数÷点P绕点O旋转的速度，可求出点P旋转到直线AB上的时间，设点Q运动的速度y cm/s，利用路程=速度×时间，可列出关于y的一元一次方程，解之即可得出结论．
本题考查了一元一次方程的应用以及两点间的距离，找准等量关系，正确列出一元一次方程是解题的关键．
21.【答案】60 30 144°
【解析】解：(1)m=6÷10%=60(人)，
n%=1860×100%=30%，
∴m=60，n=30，
故答案为：60，30；
(2)喜欢B的人数为60−18−12−6=24(人)，
喜爱《开门大吉》(B)节目所对应的扇形的圆心角的度数=360°×2460=144°，
故答案为：144°；
(3)补全图2的条形统计图如下：
(4)800×1260=160(人)．
答：喜欢《远方的家》(C)这个节目的学生有160人．
(1)从两个统计图中可知，D组的人数为6人，占调查人数的10%，可求出调查人数即m的值，A组18人占调查人数60人的比值，即可求n；
(2)用总人数乘以B组所占的百分比求出B组的人数，用360°乘以喜爱《开门大吉》节目的人数所占的百分比即可；
(3)补全条形统计图即可；
(4)用总人数乘以最喜欢《远方的家》这个节目的学生所占的百分比即可得出答案．
此题考查条形统计图、扇形统计图的制作方法以及样本估计总体的统计方法，理解统计图中各个数据之间的关系是正确解答的前提．
22.【答案】40 60%
【解析】解：(1)设A种商品每件进价为x元，
∵A种商品每件售价为60元，利润率为50%，
∴可列方程：60−x=50%x，
解得：x=40，
每件B种商品利润率=(80−50)÷50×100%=60%，
故答案为：40；60%．
(2)设购进A种商品m件，购进B种商品(70−m)件，
由题意可得：(60−40)m+(80−50)(70−m)=1580，
解得：m=52，
答：购进A种商品52件．
(3)若没有优惠促销，设小明在该商场购买同样商品要付a元，
分两种情况讨论：
①当打折前一次性购物总金额超过400元，但不超过600元时，
可列方程：0.9a=531，
解得：a=590，
②当打折前一次性购物总金额超过600元，
可列方程：600×0.8+(a−600)×0.75=531，
解得：a=668，
答：若没有优惠促销，小明在该商场购买同样商品要付590或668元．
(1)设A种商品每件进价为x元，A种商品每件售价为60元，利润率为50%，列方程即可求出x的值；根据利润率=利润÷成本×100%，可以求出每件B种商品利润率；
(2)设购进A种商品m件，购进B种商品(70−m)件，再根据总利润为1580元，列方程求解即可；
(3)若没有优惠促销，设小明在该商场购买同样商品要付a元，分两种情况讨论：①当打折前一次性购物总金额超过400元，但不超过600元时和②当打折前一次性购物总金额超过600元，分别列方程求解即可．
本题考查了一元一次方程的应用，解题的关键是仔细审题，找到等量关系并利用方程思想求解．
23.【答案】(1)是；
(2)①依题意有
(a)10t=60+12×60，
解得t=9；
(b)10t=2×60，
解得t=12；
(c)10t=60+2×60，
解得t=18．
故当t为9或12或18时，射线PM是∠QPN的“奇妙线”；
②依题意有
(a)10t=13(6t+60)，
解得t=52；
(b)10t=12(6t+60)，
解得t=307；
(c)10t=23(6t+60)，
解得t=203．
故当射线PQ是∠MPN的奇妙线时t的值为52或307或203．
【解析】解：(1)一个角的平分线是这个角的“奇妙线”；故答案为：是．
(2)①见答案;②见答案．
【分析】
(1)根据奇妙线定义即可求解；
(2)①分3种情况，根据奇妙线定义得到方程求解即可；
②分3种情况，根据奇妙线定义得到方程求解即可．
本题考查了旋转背景下，角的计算，角的平分线等，学生的阅读理解能力及知识的迁移能力．理解“奇妙线”的定义是解题的关键．打折前一次性购物总金额
优惠措施
少于等于400元
不优惠
超过400元，但不超过600元
按总售价打九折
超过600元
其中600元部分打八折优惠，超过600元的部分打七五折优惠