初中北师大版1 菱形的性质与判定教案配套ppt课件

这是一份初中北师大版1 菱形的性质与判定教案配套ppt课件，共23页。PPT课件主要包含了平行且相等，互相平分，平行四边形，轴对称，中心对称，垂直且平分，复习引入，导入新课，底×高，BC·DF等内容，欢迎下载使用。
1.能灵活运用菱形的性质定理及判定定理解决一 些相关问题,并掌握菱形面积的求法.(重点、难点)2.经历菱形性质定理及判定定理的应用过程,体会 数形结合、转化等思想方法.
1．平行四边形的对边 ，对角 ，对角线 ．2．菱形具有 的一切性质．3．菱形是 图形也是 图形．4．菱形的四条边都 ．5．菱形的两条对角线互相 ．
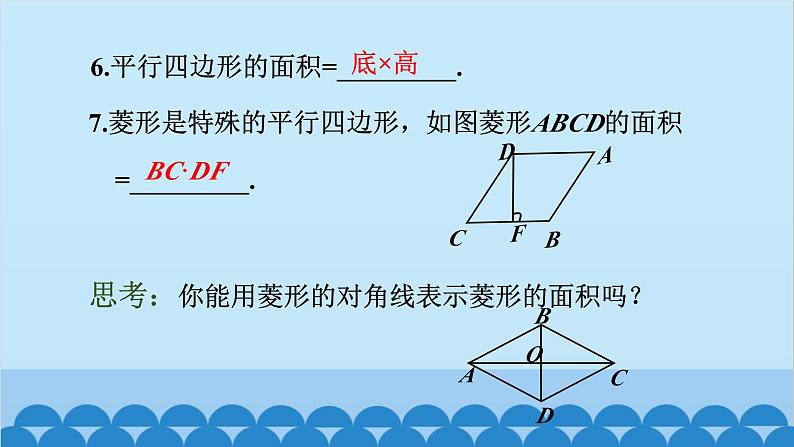
6.平行四边形的面积=_________.
7.菱形是特殊的平行四边形，如图菱形ABCD的面积 =_________.
思考：你能用菱形的对角线表示菱形的面积吗？
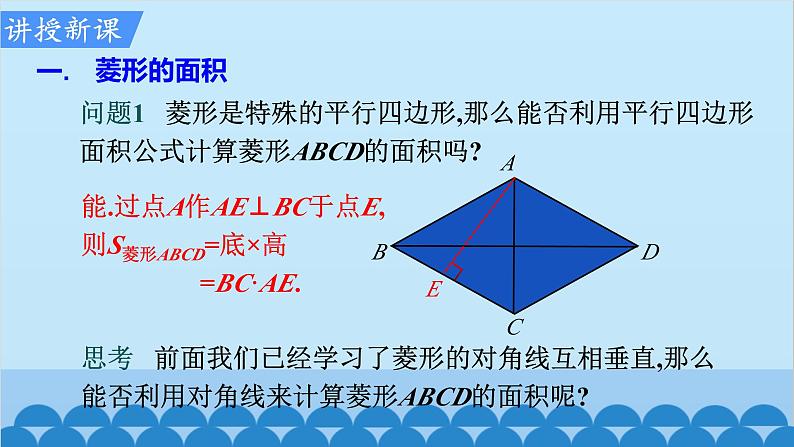
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗?
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢?
能.过点A作AE⊥BC于点E,则S菱形ABCD=底×高 =BC·AE.
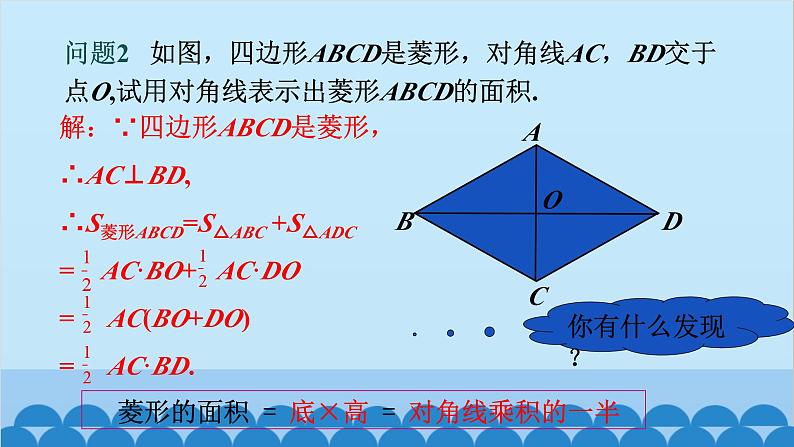
问题2 如图，四边形ABCD是菱形，对角线AC，BD交于点O,试用对角线表示出菱形ABCD的面积.
解：∵四边形ABCD是菱形，∴AC⊥BD,∴S菱形ABCD=S△ABC +S△ADC= AC·BO+ AC·DO= AC(BO+DO)= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
例1：如图,四边形ABCD是边长为13cm的菱形,其中对角线 BD长10cm.
求:(1)对角线AC的长度; (2)菱形ABCD的面积.
∵四边形ABCD是菱形,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
菱形的面积计算有如下方法：(1)一边长与两对边的距离(即菱形的高)的积；(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍)；(3)两条对角线长度乘积的一半．
例2 如图，菱形花坛ABCD的边长为20m，∠ABC＝60°，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（结果分别精确到0.01m和0.1m2 ）.
解：∵花坛ABCD是菱形，
【变式题】 如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．求：（1）两条对角线的长度；（2）菱形的面积．
解：（1）∵四边形ABCD是菱形，∴AB=BC，AC⊥BD，AD∥BC，∴∠ABC+∠BAD=180°.∵∠ABC与∠BAD的度数比为1：2，∴∠ABC= ×180°=60°，∴∠ABO= ×∠ABC=30°，△ABC是等边三角形.∵菱形ABCD的周长是8cm．∴AB=2cm，
∴OA= AB=1cm，AC=AB=2cm， ∴BD=2OB= cm；（2）S菱形ABCD= AC•BD = ×2× = （cm2）．
菱形中的相关计算通常转化为直角三角形或等腰三角形，当菱形中有一个角是60°时，菱形被分为以60°为顶角的两个等边三角形.
如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（　　） C.5cm
如图两张不等宽的纸条交叉重叠在一起，重叠的部分是什么图形？
如图两张等宽的纸条交叉重叠在一起，重叠的部分ABCD是什么图形？为什么？
分析：易知四边形ABCD是平行四边形，只需证一组邻边相等或对角线互相垂直即可.
由题意可知BC边上的高和CD边上的高相等，
然后通过证△ABE≌△ADF，即得AB=AD.
例3 如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF.(1)求证：四边形BCFE是菱形；
(1)证明：∵D、E分别是AB、AC的中点，∴DE∥BC且2DE＝BC.又∵BE＝2DE，EF＝BE，∴EF＝BC，EF∥BC，∴四边形BCFE是平行四边形．又∵EF＝BE，∴四边形BCFE是菱形；
(2)解：∵∠BCF＝120°，∴∠EBC＝60°，∴△EBC是等边三角形，∴菱形的边长为4，高为 ，∴菱形的面积为 .
(2)若CE＝4，∠BCF＝120°，求菱形BCFE的面积．
判定一个四边形是菱形时，要结合条件灵活选择方法．如果可以证明四条边相等，可直接证出菱形；如果只能证出一组邻边相等或对角线互相垂直，可以先尝试证出这个四边形是平行四边形．
如图，在平行四边形ABCD中，AC平分∠DAB，AB=2，求平行四边形ABCD的周长.
解：∵四边形ABCD为平行四边形，∴AD∥BC，AB∥CD，∴∠DAC=∠ACB，∠BAC=∠ACD，∵AC平分∠DAB，∴∠DAC=∠BAC，∴∠DAC=∠ACD，∴AD=DC，∴四边形ABCD为菱形，∴四边形ABCD的周长=4×2=8．
1.已知菱形的周长是24cm，那么它的边长是______.
2.如图，菱形ABCD中∠BAC＝120°，则∠BAC＝_______.
3.如图，菱形的两条对角线长分别为10cm和24cm，则菱形的边长是（ ）
A.10cm B.24cm C. 13cm D.17cm
4. 如图，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
解：在Rt△AOB中，OA＝5，OB＝12，∴S△AOB＝ OA·OB＝ ×5×12＝30，∴S菱形ABCD＝4S△AOB＝4×30＝120.∵又∵菱形两组对边的距离相等，∴S菱形ABCD＝AB·h＝13h，∴13h＝120，得h＝ .
5.如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD =6，求菱形的边长AB和对角线AC的长.解：∵四边形ABCD是菱形， ∴AC⊥BD(菱形的对角线互相垂直) OB=OD= BD = ×6=3 (菱形的对角线互相平分)在等腰三角形ABC中，∵∠BAD=60°，∴△ABD是等边三角形.∴AB = BD = 6.
在RtΔAOB中，由勾股定理，得OA2+OB2=AB2，∴OA = = =∴AC=2OA= （菱形的对角线相互平分）.