物理4 洛伦兹力的应用复习练习题

这是一份物理4 洛伦兹力的应用复习练习题，共9页。试卷主要包含了解析等内容，欢迎下载使用。


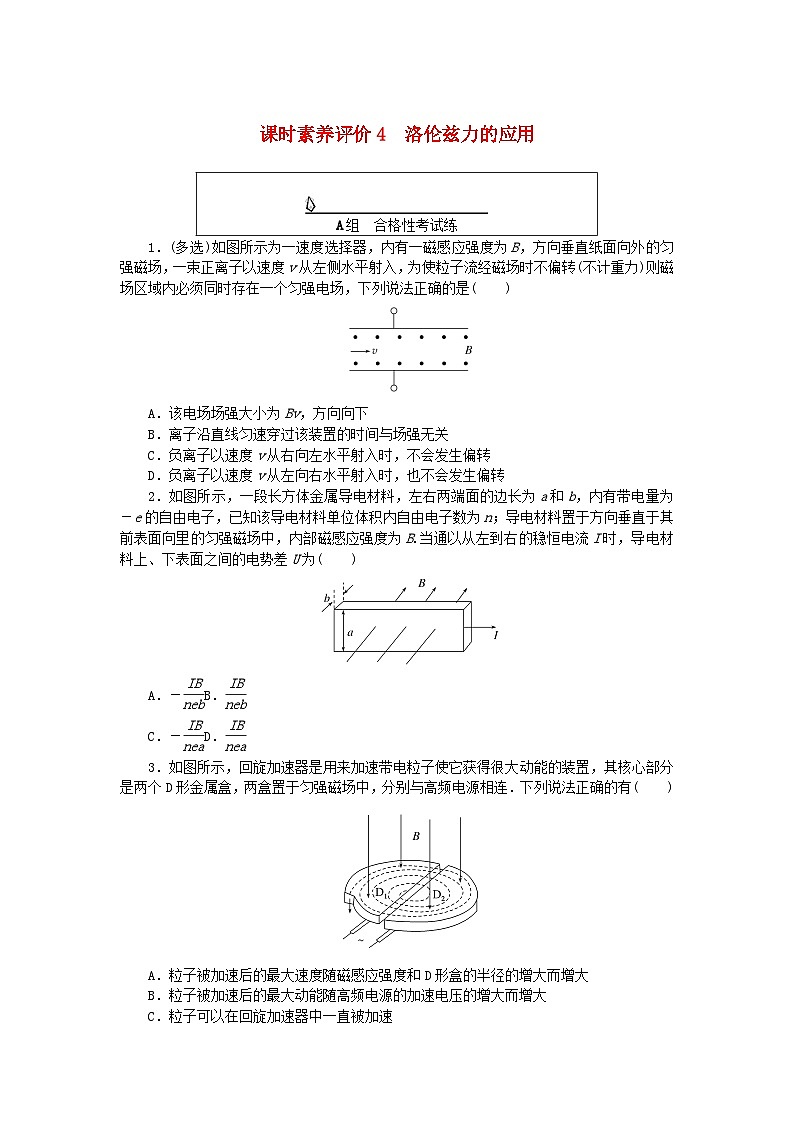
A．该电场场强大小为Bv，方向向下
B．离子沿直线匀速穿过该装置的时间与场强无关
C．负离子以速度v从右向左水平射入时，不会发生偏转
D．负离子以速度v从左向右水平射入时，也不会发生偏转
2．如图所示，一段长方体金属导电材料，左右两端面的边长为a和b，内有带电量为－e的自由电子，已知该导电材料单位体积内自由电子数为n；导电材料置于方向垂直于其前表面向里的匀强磁场中，内部磁感应强度为B.当通以从左到右的稳恒电流I时，导电材料上、下表面之间的电势差U为( )
A．－eq \f(IB,neb)B．eq \f(IB,neb)
C．－eq \f(IB,nea)D．eq \f(IB,nea)
3．如图所示，回旋加速器是用来加速带电粒子使它获得很大动能的装置，其核心部分是两个D形金属盒，两盒置于匀强磁场中，分别与高频电源相连．下列说法正确的有( )
A．粒子被加速后的最大速度随磁感应强度和D形盒的半径的增大而增大
B．粒子被加速后的最大动能随高频电源的加速电压的增大而增大
C．粒子可以在回旋加速器中一直被加速
D．粒子从磁场中获得能量
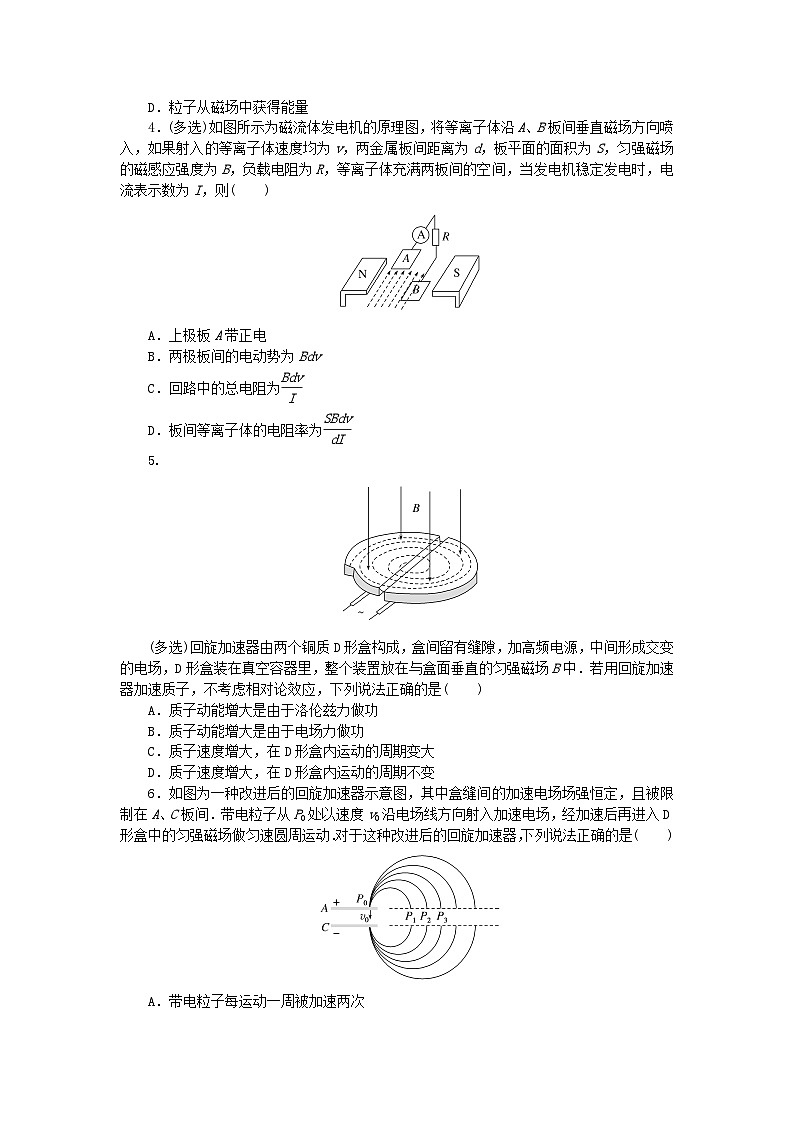
4．(多选)如图所示为磁流体发电机的原理图，将等离子体沿A、B板间垂直磁场方向喷入，如果射入的等离子体速度均为v，两金属板间距离为d，板平面的面积为S，匀强磁场的磁感应强度为B，负载电阻为R，等离子体充满两板间的空间，当发电机稳定发电时，电流表示数为I，则( )
A．上极板A带正电
B．两极板间的电动势为Bdv
C．回路中的总电阻为eq \f(Bdv,I)
D．板间等离子体的电阻率为eq \f(SBdv,dI)
5.
(多选)回旋加速器由两个铜质D形盒构成，盒间留有缝隙，加高频电源，中间形成交变的电场，D形盒装在真空容器里，整个装置放在与盒面垂直的匀强磁场B中．若用回旋加速器加速质子，不考虑相对论效应，下列说法正确的是( )
A．质子动能增大是由于洛伦兹力做功
B．质子动能增大是由于电场力做功
C．质子速度增大，在D形盒内运动的周期变大
D．质子速度增大，在D形盒内运动的周期不变
6．如图为一种改进后的回旋加速器示意图，其中盒缝间的加速电场场强恒定，且被限制在A、C板间．带电粒子从P0处以速度v0沿电场线方向射入加速电场，经加速后再进入D形盒中的匀强磁场做匀速圆周运动．对于这种改进后的回旋加速器，下列说法正确的是( )
A．带电粒子每运动一周被加速两次
B．P1P2＝P2P3
C．加速粒子的最大速度与D形盒的尺寸有关
D.加速电场方向需要做周期性的变化
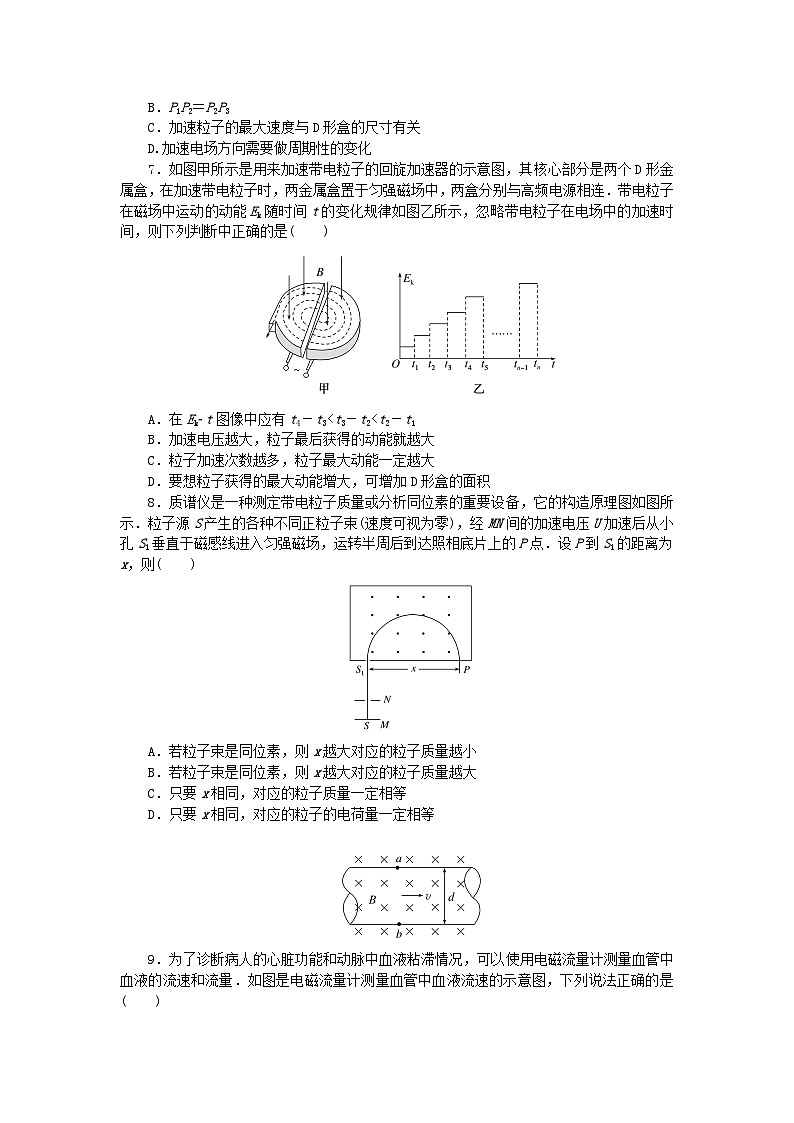
7．如图甲所示是用来加速带电粒子的回旋加速器的示意图，其核心部分是两个D形金属盒，在加速带电粒子时，两金属盒置于匀强磁场中，两盒分别与高频电源相连．带电粒子在磁场中运动的动能Ek随时间t的变化规律如图乙所示，忽略带电粒子在电场中的加速时间，则下列判断中正确的是( )
A．在Ek­t图像中应有t4－t3B．加速电压越大，粒子最后获得的动能就越大
C．粒子加速次数越多，粒子最大动能一定越大
D．要想粒子获得的最大动能增大，可增加D形盒的面积
8．质谱仪是一种测定带电粒子质量或分析同位素的重要设备，它的构造原理图如图所示．粒子源S产生的各种不同正粒子束(速度可视为零)，经MN间的加速电压U加速后从小孔S1垂直于磁感线进入匀强磁场，运转半周后到达照相底片上的P点．设P到S1的距离为x，则( )
A．若粒子束是同位素，则x越大对应的粒子质量越小
B．若粒子束是同位素，则x越大对应的粒子质量越大
C．只要x相同，对应的粒子质量一定相等
D．只要x相同，对应的粒子的电荷量一定相等
9．为了诊断病人的心脏功能和动脉中血液粘滞情况，可以使用电磁流量计测量血管中血液的流速和流量．如图是电磁流量计测量血管中血液流速的示意图，下列说法正确的是( )
A．a端电势高于b端电势
B．血液越粘滞，ab端电势差越大
C．外加磁场越大，ab两端电势差越小
D．液体均可以使用电磁流量计测量流量
10.如图所示，在一个很小的矩形半导体薄片上，作四个电极E、F、M、N，它就成了一个霍尔元件．在E、F间通入恒定的电流I，同时外加与薄片垂直的磁场B，则薄片中的载流子在洛伦兹力的作用下，向着与电流和磁场都垂直的方向漂移，使M、N间出现了电压，称为霍尔电压UH.下列关于霍尔电压大小的说法正确的是( )
A．B越大则UH越大，与I的大小无关
B．I越大则UH越大，与B的大小无关
C．在电流I、磁场B一定时，薄片的厚度越大，则UH越大
D．在电流I、磁场B一定时，薄片的厚度越大，则UH越小
11．(多选)如图所示为某种质谱仪的工作原理示意图．此质谱仪由以下几部分构成：粒子源N；P、Q间的加速电场；静电分析器；磁感应强度为B的有界匀强磁场，方向垂直纸面向外；胶片M.若静电分析器通道中心线半径为R，通道内的均匀辐射电场在中心线处的电场强度大小为E.由粒子源发出一质量为m、电荷量为q的正离子(初速度为零，重力不计)，经加速电场加速后，垂直场强方向进入静电分析器，在静电分析器中，离子沿中心线做匀速圆周运动，而后由S点沿着既垂直于静电分析器的左边界，又垂直于磁场的方向射入磁场中，最终打到胶片上的某点．下列说法中正确的是( )
A．P、Q间加速电压为eq \f(1,2)ER
B．离子在磁场中运动的半径为eq \r(\f(mER,q))
C．若一质量为4m、电荷量为q的正离子加速后进入静电分析器，离子不能从S点射出
D．若一群离子经过上述过程打在胶片上同一点，则这些离子具有相同的比荷
12.质谱仪原理如图所示，a为粒子加速器，电压为U1；b为速度选择器，磁场与电场正交，磁感应强度为B1，板间距离为d；c为偏转分离器，磁感应强度为B2.今有一质量为m、电荷量为e的正粒子(不计重力)，经加速后，该粒子恰能通过速度选择器，粒子进入分离器后做匀速圆周运动．求：
(1)粒子的速度v；
(2)速度选择器的电压U2；
(3)粒子在分离器磁场中做匀速圆周运动的半径R.
13．如图所示为回旋加速器的示意图．它由两个铝制D形金属扁盒组成，两个D形盒正中间开有一条狭缝，两个D形盒处在匀强磁场中并接在高频交变电源上．在D1盒中心A处有一粒子源，它产生并发出的α粒子经狭缝电压加速后，进入D2盒中，在磁场力的作用下运动半个圆周后，再次经狭缝电压加速．为保证粒子每次经过狭缝都被加速，设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致．如此周而复始，速度越来越大，运动半径也越来越大，最后到达D形盒的边缘，以最大速度被导出．已知α粒子电荷量为q，质量为m，加速时电极间电压大小恒为U，磁场的磁感应强度为B，D形盒的半径为R，设狭缝很窄，粒子通过狭缝的时间可以忽略不计，且α粒子从粒子源发出时的初速度为零．(不计α粒子重力)求：
(1)α粒子第1次由D1盒进入D2盒中时的速度大小；
(2)α粒子被加速后获得的最大动能Ek；
(3)符合条件的交变电压的周期T；
(4)粒子仍在盒中活动过程中，α粒子在第n次由D2盒进入D1盒的位置与紧接着第n＋1次由D2盒进入D1盒位置之间的距离Δx.
课时素养评价4 洛伦兹力的应用
1．解析：为使粒子不发生偏转，粒子所受到的电场力和洛伦兹力是平衡力，即qvB＝qE，所以电场强度大小与磁感应强度大小的关系为E＝vB，根据左手定则，得洛伦兹力方向向下，所以电场力必须向上，粒子带正电，故电场强度向上，A错误；设装置长度为L，则离子沿直线匀速穿过该装置的时间为t＝eq \f(L,v)，时间与场强无关，B正确；负离子从右向左以速度v水平射入时，洛伦兹力和电场力的方向都向下，所以受力不再平衡，将发生偏转，C错误；负离子从左向右以速度v水平射入时，洛伦兹力向上，电场力向下，还是受力平衡，所以负离子不会发生偏转，D正确．
答案：BD
2．解析：根据题意，由左手定则可知，负电荷向上表面偏转，上表面带负电，下表面带正电，所以上表面比下表面电势低，最终电子在电场力和洛伦兹力作用下处于平衡有evB＝eeq \f(U,a)，由电流微观表达式有I＝neSv＝neabv，联立解得U＝－eq \f(IB,neb)，A正确．
答案：A
3．解析：根据qvB＝meq \f(v2,R)得，最大速度v＝eq \f(qBR,m)，则最大动能Ekm＝eq \f(1,2)mv2＝eq \f(q2B2R2,2m)，最大动能随金属盒的半径以及磁感应强度的增大而增大，与加速的次数和加速电压的大小无关，A正确，B错误；粒子在加速器中加速到在磁场中的半径等于D形盒的半径时就不能再加速了，所以粒子在回旋加速器中不是一直被加速，C错误；粒子在磁场中受到洛伦兹力，其对粒子不做功，不能获得能量，D错误．
答案：A
4．解析：由左手定则可得下极板带正电，A错误；由洛伦兹力与电场力平衡可得qvB＝qeq \f(U,d)，解得U＝Bdv，则两极板间的电动势为Bdv，B正确；回路中的电阻为R总＝eq \f(U,I)＝eq \f(Bdv,I)，C正确；板间等离子体的电阻R1＝R总－R，由电阻定律有R1＝ρeq \f(d,S)，解得ρ＝eq \f(（Bdv－IR）S,Id)，D错误．
答案：BC
5．解析：洛伦兹力始终与速度垂直，即洛伦兹力对粒子不做功，而电场力对粒子做功，即质子动能增大是由于电场力做功，A错误，B正确；由Bqv＝meq \f(v2,r)，T＝eq \f(2πr,v)，可以得到T＝eq \f(2πm,qB)，即周期与速度无关，C错误，D正确．
答案：BD
6．解析：带电粒子只有经过AC板间时被加速，即带电粒子每运动一周被加速一次．电场的方向没有改变，则在AC间加速，A、D错误；根据洛伦兹力提供向心力qvB＝meq \f(v2,r)，可得r＝eq \f(mv,qB)，所以P1P2＝2(r2－r1)＝eq \f(2mΔv,qB)，因为每转一圈被加速一次，根据速度位移关系v2－v eq \\al(\s\up1(2),\s\d1(1)) ＝2ad，可知每转一圈，速度的变化量不等，且v3－v2P2P3，B错误；当粒子从D形盒中射出时，速度最大，则qvB＝meq \f(v2,R)，可得v＝eq \f(qBR,m)，由此可知，加速粒子的最大速度与D形盒的半径有关，C正确．
答案：C
7．解析：带电粒子在匀强磁场中做匀速圆周运动的周期与速度大小无关，因此，在Ek­t图中应有t4－t3＝t3－t2＝t2－t1，A错误；粒子获得的最大动能与加速电压无关，加速电压越小，粒子加速次数就越多，由粒子做圆周运动的半径r＝eq \f(mv,qB)＝eq \f(\r(2mEk),qB)，可知Ek＝eq \f(q2B2r2,2m)，即粒子获得的最大动能决定于D形盒的半径，当轨道半径r与D形盒半径R相等时就不能继续加速，B、C错误，D正确．
答案：D
8．解析：粒子在加速电场中做加速运动，由动能定理得：qU＝eq \f(1,2)mv2，解得：v＝eq \r(\f(2qU,m)).粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：qvB＝eq \f(mv2,r)，可得：r＝eq \f(mv,qB)＝eq \f(1,B)eq \r(\f(2Um,q))，所以：x＝2r＝eq \f(2,B)eq \r(\f(2Um,q))；若粒子束是同位素，则q相同而m不同，x越大对应的粒子质量越大，A错误，B正确．由x＝eq \f(2,B)eq \r(\f(2Um,q))可知，只要x相同，对应的粒子的比荷一定相等，粒子质量和电荷量不一定相等，C、D错误．
答案：B
9．解析：血液中正负离子向右流动的速度为v，根据左手定则，在洛伦兹力作用下，正离子向管道a的一侧集中，而负离子向管道b的一侧集中，两者之间形成电势差，则a端电势高于b端电势，A正确；当正负离子受到的电场力与洛伦兹力平衡时，离子不再偏移，此时有稳定的电势差，形成一个匀强电场，对离子有qvB＝qeq \f(U,d)，解得U＝vBd，血液越粘滞，v越小，ab端电势差越小，B错误；根据U＝vBd，外加磁场越大，ab两端电势差越大，故C错误；根据U＝vBd，得v＝eq \f(U,Bd).设在时间Δt内流进管道的血液体积为V，则流量Q＝eq \f(V,Δt)＝eq \f(π（\f(d,2)）2v·Δt,Δt)，联立解得Q＝eq \f(πdU,4B)，若液体不含带电粒子，不可以使用电磁流量计测量流量，D错误．
答案：A
10．解析：设M、N间距离为d，薄片的厚度为x，当达到稳定状态，载流子受力平衡，满足qeq \f(UH,d)＝qvB，又有电流的微观表达式I＝nqvS＝nqv·dx，联立可得UH＝eq \f(BI,nqx)，与B、I均有关系，A、B错误；由上述分析可知，在电流I、磁场B一定时，薄片的厚度x越大，则UH越小，C错误，D正确．
答案：D
11．解析：离子在加速电场中加速，根据动能定理，有
qU＝eq \f(1,2)mv2 ①，
电场中的偏转过程，电场力提供向心力，根据牛顿第二定律，有qE＝meq \f(v2,R) ②，
磁场中的偏转过程，洛伦兹力提供向心力，根据牛顿第二定律，有qvB＝meq \f(v2,r) ③，
由①②解得U＝eq \f(1,2)ER ④.
由②③解得r＝eq \f(m,qB)eq \r(\f(qER,m))＝eq \f(1,B)eq \r(\f(mER,q))⑤，由④式可知，只要满足R＝eq \f(2U,E)，所有粒子都可以在弧形电场区通过；因r＝eq \f(1,B)eq \r(\f(mER,q))，故打到胶片上同一点的粒子的比荷一定相等，A、D正确，B、C错误．
答案：AD
12．解析：(1)在电场中，粒子被加速电场加速，由动能定理有eU1＝eq \f(1,2)mv2
解得粒子的速度v＝eq \r(\f(2eU1,m)).
(2)在速度选择器中，粒子受的电场力和洛伦兹力大小相等，则有eeq \f(U2,d)＝evB1
解得速度选择器的电压U2＝B1dv＝B1deq \r(\f(2eU1,m)).
(3)在磁场中，粒子受洛伦兹力作用而做圆周运动，则有evB2＝eq \f(mv2,R)
解得半径R＝eq \f(mv,eB2)＝eq \f(1,B2)eq \r(\f(2mU1,e)).
答案：(1)eq \r(\f(2eU1,m)) (2)B1deq \r(\f(2eU1,m)) (3)eq \f(1,B2)eq \r(\f(2mU1,e))
13．解析：(1)设α粒子第一次被加速后进入D2盒中时的速度大小为v1，根据动能定理有
qU＝eq \f(1,2)mv eq \\al(\s\up1(2),\s\d1(1))
解得v1＝eq \r(\f(2qU,m)).
(2)α粒子在D形盒内做圆周运动，轨道半径达到最大时被引出，具有最大动能．设此时的速度为v，有
qvB＝eq \f(mv2,R)
解得v＝eq \f(qBR,m)
设α粒子的最大动能为Ek，则Ek＝eq \f(1,2)mv2
解得Ek＝eq \f(q2B2R2,2m).
(3)为保证粒子每次经过狭缝都被加速，带电粒子在磁场中运动一周的时间应等于交变电压的周期(在狭缝的时间极短，忽略不计)，则交变电压的周期T＝eq \f(2πr,v)＝eq \f(2πm,Bq).
(4)离子经电场第1次加速后，以速度v1进入D2盒，设轨道半径为r1，则r1＝eq \f(mv1,qB)＝eq \f(1,B)eq \r(\f(2mU,q))
离子经第2次电场加速后，以速度v2进入D1盒，设轨道半径为r2，则r2＝eq \f(mv2,qB)＝eq \f(1,B)eq \r(\f(2×2mU,q))
离子第n次由D1盒进入D2盒，离子已经过(2n－1)次电场加速，以速度v2n－1进入D2盒，由动能定理得
(2n－1)Uq＝eq \f(1,2)mv eq \\al(\s\up1(2),\s\d1(2n－1))
轨道半径rn＝eq \f(mv2n－1,qB)＝eq \f(1,B)eq \r(\f(（2n－1）2mU,q))
离子经第n＋1次由D1盒进入D2盒，离子已经过2n次电场加速，以速度v2n进入D1盒，由动能定理得
2nUq＝eq \f(1,2)mv eq \\al(\s\up1(2),\s\d1(2n))
轨道半径rn＋1＝eq \f(mv2n,qB)＝eq \f(1,B)eq \r(\f(2n·2mU,q))
则Δx＝2(rn＋1－rn)(如图所示)
解得Δx＝eq \f(2,B)eq \r(\f(2Um,q))(eq \r(2n)－eq \r(2n－1)).
答案：(1) eq \r(\f(2qU,m)) (2)eq \f(q2B2R2,2m) (3)eq \f(2πm,Bq)
(4)eq \f(2,B)eq \r(\f(2Um,q))(eq \r(2n)－eq \r(2n－1))
A组 合格性考试练
B组 选择性考试练