2023-2024学年辽宁省丹东市宽甸满族自治县八年级（上）学期期末数学试题（含解析）

这是一份2023-2024学年辽宁省丹东市宽甸满族自治县八年级（上）学期期末数学试题（含解析），共21页。
1、考生须诚信考试,遵守考场规则和考试纪律，并自觉服从监考教师和其他考试工作人员
管理；
2、监考教师发卷后，在试卷指定的地方填写本人准考证号、姓名等信息；考试中途考生不准以任何理由离开考场；
3、考生答卷用笔必须使用同一规格同一颜色的笔作答(作图可使用铅笔) ，不准用规定以外的笔答卷，不准在答卷上作任何标记。考生书写在答题卡规定区域外的答案无效。
4、考试开始信号发出后,考生方可开始作答。
一、选择题（每小题3分，共30分）
1．16的平方根是（ ）
A．±16B．±8C．±4D．±2
2．下列实数中，（ ）是无理数．
A．﹣3.1416B．C．﹣D．
3．下列各组数分别是三条线段的长度，其中能围成直角三角形的是（ ）．
A．1，1，2B．1，2，3C．1，，D．2，3，4
4．将三角形三个顶点的横坐标都减2，纵坐标不变，则所得三角形与原三角形的关系是（ ）
A．将原图向左平移两个单位B．关于原点对称
C．将原图向右平移两个单位D．关于y轴对称
5．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（ ）
A．50°B．65°C．75°D．80°
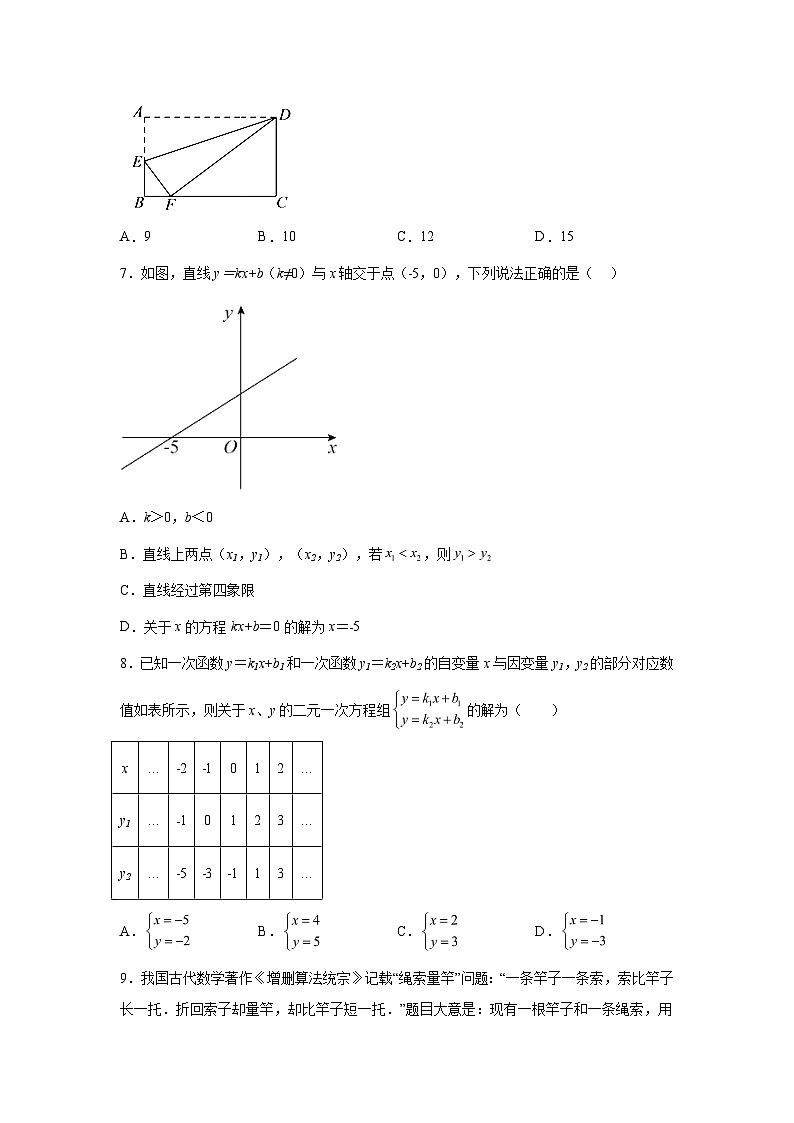
6．如图，在长方形ABCD中，点E在AB边上，将长方形ABCD沿直线DE折叠，点A恰好落在BC边上的点F处．若AE=5，BF=3，则CF的长为（ ）
A．9B．10C．12D．15
7．如图，直线y＝kx+b（k≠0）与x轴交于点（﹣5，0），下列说法正确的是（ ）
A．k＞0，b＜0
B．直线上两点（x1，y1），（x2，y2），若，则
C．直线经过第四象限
D．关于x的方程kx+b＝0的解为x＝﹣5
8．已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1，y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（ ）
A．B．C．D．
9．我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托．”题目大意是：现有一根竿子和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短了5尺．设竿长为x尺，绳索长为y尺，则符合题意的方程组是（ ）
A．B．C．D．
10．如图1，点从的顶点出发，沿匀速运动到点A，图2是点运动时，线段的长度随时间变化的关系图像，其中是曲线部分的最低点，则的面积是（ ）
A．72B．78C．84D．90
二、填空题（本题共5小题，每小题3分，共15分）
11．比较实数的大小：3 （填“＞”、“＜”或“＝”）．
12．若二次根式有意义，则的取值范围是 ．
13．农科院计划为某地选择合适的水果玉米种子，通过试验，甲、乙、丙、丁四种水果玉米种子每亩平均产量都是1500千克，方差分别为，，，，这四种水果玉米种子中产量最稳定的是 种水果玉米种子．
14．数轴是一个非常重要的数学工具，揭示了数与点之间的内在联系，它是“数形结合”的基础．如图所示，面积为5的正方形的顶点A在数轴上，且点A表示的数为1，若点在数轴上（点在点A左侧），且，则点所表示的数为 ．
15．对于平面直角坐标系中的点P（x，y），若x，y满足|x﹣y|＝5，则点P（x，y）就称为“平衡点”．例如：（1，6），因为|1﹣6|＝5，所以（1，6）是“平衡点”．已知一次函数y＝3x+k（k为常数）图象上有一个“平衡点”的坐标是（3，8），则一次函数y＝3x+k（k为常数）图象上另一“平衡点”的坐标是 ．
三、解答题（本题共8小题，共75分，解答题应写出文字说明、演算步骤或推理过程）
16．按要求解答下列各题.
(1)计算：．
(2)解方程组：．
17．如图，在平面直角坐标系中，的三个顶点分别为．
(1)请在图中作出关于轴对称的，并直接写出点A的对应点的坐标；
(2)求出的面积；
(3)在轴上有一点，使得的周长最小，在图中找出点的位置，并直接写出的周长最小值．
18．如图，在△ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H，∠CDG＝∠B，∠1＋∠FEA＝180°．求证：
（1）EH∥AD；
（2）∠BAD＝∠H．
19．2021年6月26日是第34个国际禁毒日，为了解同学们对禁毒知识的掌握情况，学校开展了禁毒知识讲座和知识竞赛，从全校1800名学生中随机抽取部分学生的竞赛试卷进行调查分析，并将成绩（满分：100分）制成如图所示的扇形统计图和条形统计图．
请根据统计图回答下列问题：
(1)求出随机被抽查的学生总数，并补全上面不完整的条形统计图；
(2)这些学生成绩的中位数是______分；众数是______分；
(3)根据比赛规则，96分以上的学生有资格进入第二轮知识竞赛环节，请你估计全校1800名学生进入第二轮环节的人数是多少？
20．如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点N沿路线O→A→C运动.
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）当△ONC的面积是△OAC面积的时，求出这时点N的坐标．
21．随着“互联网”时代的到来，一种新型打车方式受到大众欢迎，该打车方式的总费用由里程费和耗时费组成，其中里程费按x元/公里计算，耗时贵按y元/分钟计算（总费用不足9元按9元计价），小明、小刚两人用该打车方式出行，按上述计价规则，其打车总费用、行驶里程数与打车时间如表：
(1)求x，y的值；
(2)如果小华也用该打车方式，打车行驶了12公里，用了16分钟，那么小华的打车总费用为多少？
22．【问题提出】
小明在学习一次函数后，对形如（其中为常数，且）的一次函数产生了兴趣，于是对它的图像和性质进行了探究，过程如下：
【特例探究】
(1)如图所示，小明已经分别画出了函数，，的图像．
请你先完成下侧列表，然后再描点、连线在图中画出函数的图像．
【深入探究】
(2)通过对上述几个函数图像的观察、思考，你发现（为常数，且）的图像一定会经过的点的坐标是______．
【总结经验】
(3)类比上述探究结果，推理函数（其中为常数，且）的图像一定会经过的点的坐标是______．
【实践运用】
(4)已知一次函数（为常数，且）的图像一定过点，且与轴相交于点，若的面积为2，求出的值．
23．【数学模型】
“8字型”是初中数学“图形与几何”中的常用模型，通常由一组对顶角所在的两个三角形构成．如图1，交于点，根据“三角形内角和是”，不难得出两个三角形中的角存在以下关系：①（对顶角相等）；②．
【提出问题】分别作出和的平分线，两条角平分线交于点，如图2，与，之间是否存在某种数量关系呢？
【解决问题】为了解决上面的问题，我们从特例开始探究．已知的平分线与的平分线交于点．
(1)如图2，，，则的度数是多少呢？
易证，
请你完成后续的推理过程：
______
，分别是，的平分线
，
______
又，
______度．
(2)在总结前面问题的基础上，借助图2，直接写出与，之间的数量关系是： ______．
【类比应用】
(3)如图3，的平分线与的平分线交于点．
已知：，，则______．（用、表示）
参考答案与解析
1．C
【分析】根据平方根的性质：正数a有两个平方根，它们互为相反数，求解即可．
【详解】解：∵（±4）2=16，
∴16的平方根是±4．
故选：C．
【点睛】本题主要考查了平方根，熟练掌握平方根的性质：正数a有两个平方根，它们互为相反数，是解题关键．
2．B
【分析】根据无理数的概念判断即可.
【详解】解：A、﹣3.1416是有限小数，属于有理数，故本选项不合题意；
B、是无理数，故本选项符合题意；
C. ﹣=-2，是整数，属于有理数，故本选项不合题意；
D. 是分数，属于有理数，故本选项不合题意．
故选：B．
【点睛】本题考查无理数的概念,关键在于熟练掌握概念.
3．C
【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】解：A、12+12≠22，故不是直角三角形，故此选项不符合题意；
B、12+22≠32，故不是直角三角形，故此选项不符合题意；
C、12+（）2=（）2，故是直角三角形，故此选项符合题意；
D、22+32≠42，故不是直角三角形，故此选项不符合题意．
故选：C．
【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
4．A
【分析】根据坐标与图形变化，把三角形三个顶点的横坐标都减2，纵坐标不变，就是把三角形向左平移2个单位，大小不变，形状不变．
【详解】解：∵将三角形三个顶点的横坐标都减2，纵坐标不变，
∴所得三角形与原三角形的关系是：将原图向左平移两个单位．
故选：A．
5．B
【分析】根据题意得：BG∥AF，可得∠FAE=∠BED=50°，再根据折叠的性质，即可求解．
【详解】解：如图，
根据题意得：BG∥AF，
∴∠FAE=∠BED=50°，
∵AG为折痕，
∴ ．
故选：B
【点睛】本题主要考查了图形的折叠，平行线的性质，熟练掌握两直线平行，同位角相等；图形折叠前后对应角相等是解题的关键．
6．C
【详解】∵四边形ABCD是长方形，
∴∠B=∠C=∠A=90°，AB=CD，
由折叠的性质可得：EF=AE=5，∠EFD=∠A=90°，
在Rt△BEF中，BE==4，∠BFE+∠BEF=90°，
∴CD=AB=AE+BE=5+4=9，
∵∠EFD=90°，∴∠BFE+∠DFC=90°，
∴∠BEF=∠CFD，
∴△BEF∽△CFD，
∴，即 ，
∴CF=12，
故选C.
7．D
【分析】根据一次函数的性质，一次函数与方程的关系即可判断．
【详解】解：直线经过一、二、三象限，
，，故A、C错误；
直线经过一、二、三象限，
随的增大而增大，
∴，，，是直线上的两点，若，则，故B错误；
直线与轴交于点，
当时，函数，
关于的方程的解为，故D正确；
故选：D．
【点睛】本题考查了一次函数的图象和系数的关系，一次函数与一元一次方程，熟知一次函数的性质是解题的关键．
8．C
【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标解决问题．
【详解】解：由表格可知，一次函数y1=k1x+b1和一次函数y2=k2x+b2的图象都经过点(2，3)，
∴一次函数y1=k1x与y=k2x+b的图象的交点坐标为(2，3)，
∴关于x，y的二元一次方程组的解为．
故选：C．
【点睛】本题考查了一次函数图像交点坐标与方程组解的关系：对于函数y1=k1x+b1，y2=k2x+b2，其图象的交点坐标(x，y)中x，y的值是方程组的解．
9．B
【分析】根据用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短了5尺列方程．
【详解】解：设竿长为x尺，绳索长为y尺，
∵用绳索去量竿，绳索比竿长5尺；
∴
∵将绳索对半折后再去量竿，就比竿短了5尺，
∴，
故选：B．
【点睛】此题考查古代问题与二元一次方程组，正确理解题意是解题的关键．
10．C
【分析】本题考查了函数图像的应用、勾股定理等知识点，根据图形和图像信息确定相关线段长度是解题的关键．
根据图像可知点P在上运动时，此时不断增大，而从C向A运动时，先变小后变大，从而可求出、、的长度以及边边上的高，最后运用三角形的面积公式即可解答．
【详解】解：根据图像可知点P在上运动时，此时不断增大，
由图像可知：点P从B向C运动时，的最大值为，即，
由于M是曲线部分的最低点，此时最小，
如图，即，
∴由勾股定理可知：，
由于P最终到达点A，则，
∴，
∴，
∴的面积为：．
故选：C．
11．