湘教版（2019）选择性必修 第二册4.3 独立性检验综合训练题

这是一份湘教版（2019）选择性必修 第二册4.3 独立性检验综合训练题，共5页。试卷主要包含了214，058，635)≈0，167，，091>6，333>10，024等内容，欢迎下载使用。
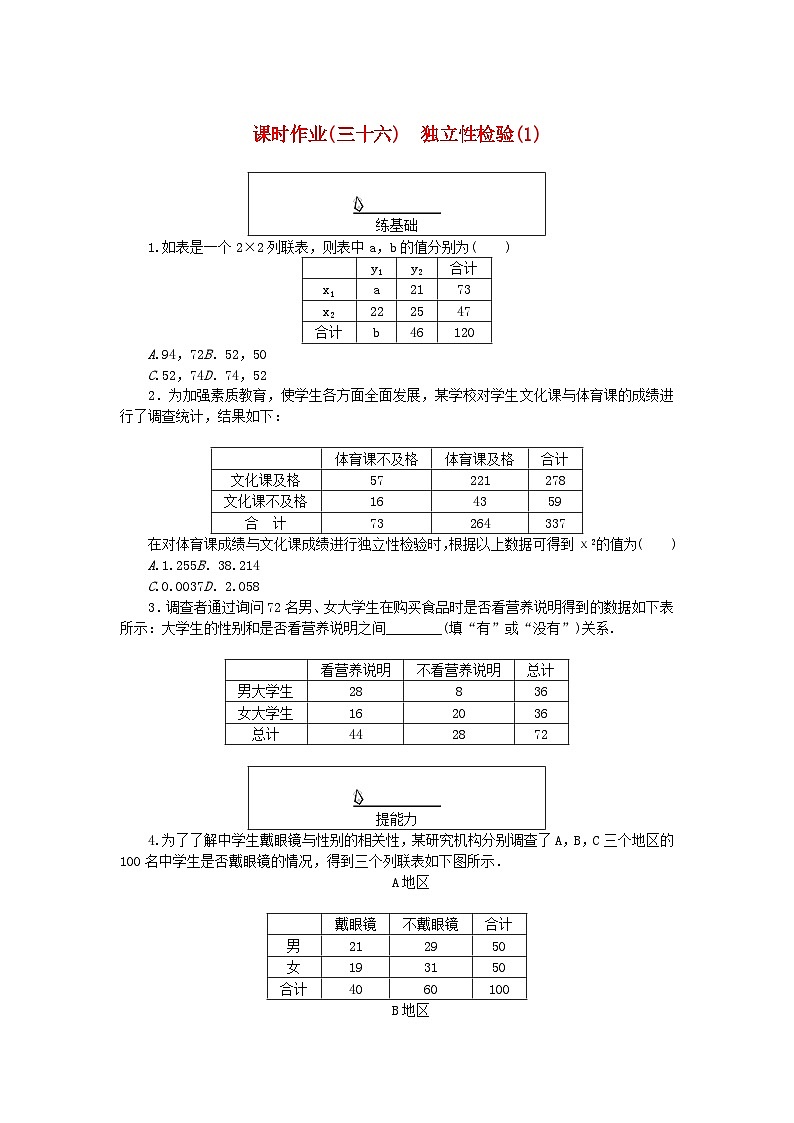
A.94，72B．52，50
C.52，74D．74，52
2．为加强素质教育，使学生各方面全面发展，某学校对学生文化课与体育课的成绩进行了调查统计，结果如下：
在对体育课成绩与文化课成绩进行独立性检验时，根据以上数据可得到χ2的值为( )
．38.214
．2.058
3．调查者通过询问72名男、女大学生在购买食品时是否看营养说明得到的数据如下表所示：大学生的性别和是否看营养说明之间________(填“有”或“没有”)关系.
4.为了了解中学生戴眼镜与性别的相关性，某研究机构分别调查了A，B，C三个地区的100名中学生是否戴眼镜的情况，得到三个列联表如下图所示．
A地区
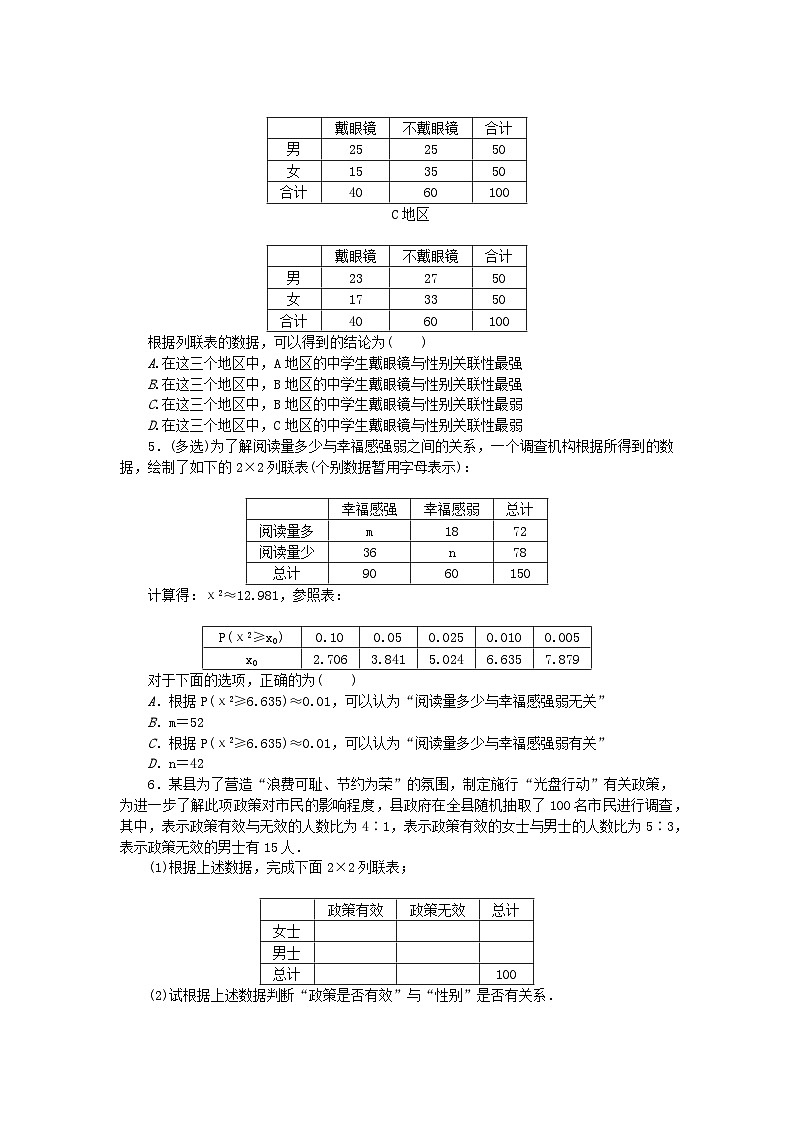
B地区
C地区
根据列联表的数据，可以得到的结论为( )
A.在这三个地区中，A地区的中学生戴眼镜与性别关联性最强
B.在这三个地区中，B地区的中学生戴眼镜与性别关联性最强
C.在这三个地区中，B地区的中学生戴眼镜与性别关联性最弱
D.在这三个地区中，C地区的中学生戴眼镜与性别关联性最弱
5．(多选)为了解阅读量多少与幸福感强弱之间的关系，一个调查机构根据所得到的数据，绘制了如下的2×2列联表(个别数据暂用字母表示)：
计算得：χ2≈12.981，参照表：
对于下面的选项，正确的为( )
A．根据P(χ2≥6.635)≈0.01，可以认为“阅读量多少与幸福感强弱无关”
B．m＝52
C．根据P(χ2≥6.635)≈0.01，可以认为“阅读量多少与幸福感强弱有关”
D．n＝42
6．某县为了营造“浪费可耻、节约为荣”的氛围，制定施行“光盘行动”有关政策，为进一步了解此项政策对市民的影响程度，县政府在全县随机抽取了100名市民进行调查，其中，表示政策有效与无效的人数比为4∶1，表示政策有效的女士与男士的人数比为5∶3，表示政策无效的男士有15人．
(1)根据上述数据，完成下面2×2列联表；
(2)试根据上述数据判断“政策是否有效”与“性别”是否有关系．
附：χ2＝eq \f(n（ad－bc）2,（a＋b）（c＋d）（a＋c）（b＋d）)，其中n＝a＋b＋c＋d.
7.某高中举办了一次“喜迎十九大”的读书读报知识竞赛，参赛选手为从高一年级和高二年级各随机抽取的100名学生．图1和图2分别是高一年级和高二年级参赛选手成绩(单位：分)的频率分布直方图．
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩；(同一组的数据用该组区间的中点值代表)
(2)完成下面的2×2列联表，并根据上述数据判断高一、高二两个年级学生这次读书读报知识竞赛的成绩是否有差异．(单位：人)
课时作业(三十六) 独立性检验(1)
1．解析：a＝73－21＝52，b＝a＋22＝52＋22＝74.故选C.
答案：C
2．解析：根据χ2＝eq \f(n（ad－bc）2,（a＋b）（c＋d）（a＋c）（b＋d）)＝1.255，故选A.
答案：A
3．解析：因为χ2＝eq \f(72×（28×20－16×8）2,44×28×36×36)≈8.416>6.635，所以认为大学生性别与购买食品时是否看营养说明之间有关．
答案：有
4．解析：由χ eq \\al(\s\up1(2),\s\d1(A)) ＝eq \f(100×（21×31－19×29）2,40×60×50×50)≈0.167，
χ eq \\al(\s\up1(2),\s\d1(B)) ＝eq \f(100×（25×35－15×25）2,40×60×50×50)≈4.167，
χ eq \\al(\s\up1(2),\s\d1(C)) ＝eq \f(100×（23×33－17×27）2,40×60×50×50)＝1.5，
∴χ eq \\al(\s\up1(2),\s\d1(B)) >χ eq \\al(\s\up1(2),\s\d1(C)) >χ eq \\al(\s\up1(2),\s\d1(A)) ，
故在这三个地区中，B地区的中学生戴眼镜与性别关联性最强，A地区的中学生戴眼镜与性别关联性最弱．故选B.
答案：B
5．解析：对于A，χ2≈12.981>6.635，可以认为“阅读量多少与幸福感强弱有关”，故A错误，C正确；对于B，m＋18＝72，m＝54，故B错误；对于D，n＝78－36＝42，正确，故选CD.
答案：CD
6．解析：(1)由题意表示政策有效的有80人，无效的有20人，
其中表示政策有效的男士为50人，女士有30人．
由此可填写出2×2列联表如下：
(2)假设H0：政策是否有效与性别没有关系，计算χ2＝eq \f(100×（30×5－15×50）2,55×45×80×20)≈9.091>6.635，故否定假设H0，所以认为政策是否有效与性别有关系．
7．解析：(1)高一年级参赛学生的平均成绩为(45×0.04＋55×0.04＋65×0.01＋75×0.01)×10＝54分，
高二年级参赛学生的平均成绩为(45×0.015＋55×0.025＋65×0.035＋75×0.025)×10＝62分．
(2)补全2×2列联表如下：单位：人
假设为H0：两个年级的成绩相互独立，即高一、高二两个年级学生这次读书读报知识竞赛的成绩没有差异．计算可得χ2＝eq \f(200×（80×60－20×40）2,100×100×120×80)≈33.333>10.828，
故否定假设H0，所以认为高一高二两个年级学生这次读书读报知识竞赛的成绩有差异．
练基础
y1
y2
合计
x1
a
21
73
x2
22
25
47
合计
b
46
120
体育课不及格
体育课及格
合计
文化课及格
57
221
278
文化课不及格
16
43
59
合 计
73
264
337
看营养说明
不看营养说明
总计
男大学生
28
8
36
女大学生
16
20
36
总计
44
28
72
提能力
戴眼镜
不戴眼镜
合计
男
21
29
50
女
19
31
50
合计
40
60
100
戴眼镜
不戴眼镜
合计
男
25
25
50
女
15
35
50
合计
40
60
100
戴眼镜
不戴眼镜
合计
男
23
27
50
女
17
33
50
合计
40
60
100
幸福感强
幸福感弱
总计
阅读量多
m
18
72
阅读量少
36
n
78
总计
90
60
150
P(χ2≥x0)
0.10
0.05
0.025
0.010
0.005
x0
2.706
3.841
5.024
6.635
7.879
政策有效
政策无效
总计
女士
男士
总计
100
P(χ2≥x0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
培优生
成绩低于60分
成绩不低于60分
合计
高一年级
高二年级
合计
政策有效
政策无效
总计
女士
50
5
55
男士
30
15
45
总计
80
20
100
成绩低于60分
成绩不低于60分
合计
高一年级
80
20
100
高二年级
40
60
100
合计
120
80
200