初中数学3.4 实际问题与一元一次方程图片课件ppt

这是一份初中数学3.4 实际问题与一元一次方程图片课件ppt，共27页。PPT课件主要包含了情景引入，典例精析，列表分析，人数和为22人，22－x，方法归纳，变式训练，32-x，做一做，总工作量等内容，欢迎下载使用。

前面我们学习了一元一次方程的解法，本节课我们将讨论一元一次方程的应用. 生活中，有很多需要进行配套的问题，如餐桌和椅子、螺钉和螺母、电扇叶片和电机轴等，大家能举出生活中配套问题的例子吗？
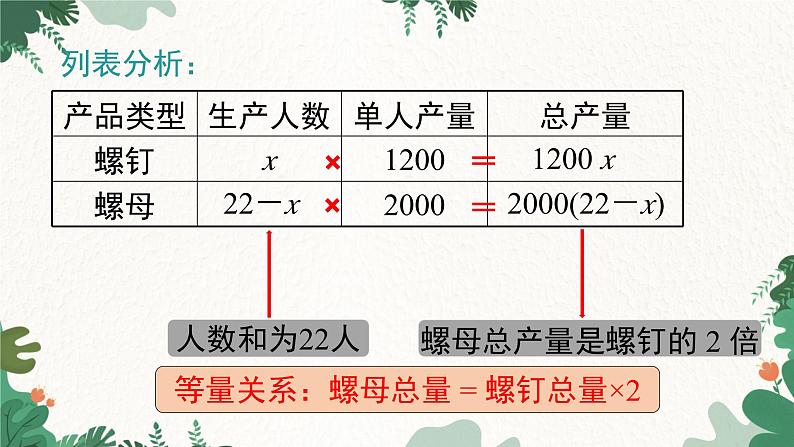
例1 某车间有 22 名工人，每人每天可以生产 1 200 个螺钉或 2 000 个螺母. 1 个螺钉需要配 2 个螺母，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各多少名？
想一想：本题需要我们解决的问题是什么？题目中哪些信息能解决人员安排的问题？螺母和螺钉的数量关系如何？
螺母总产量是螺钉的 2 倍
等量关系：螺母总量 = 螺钉总量×2
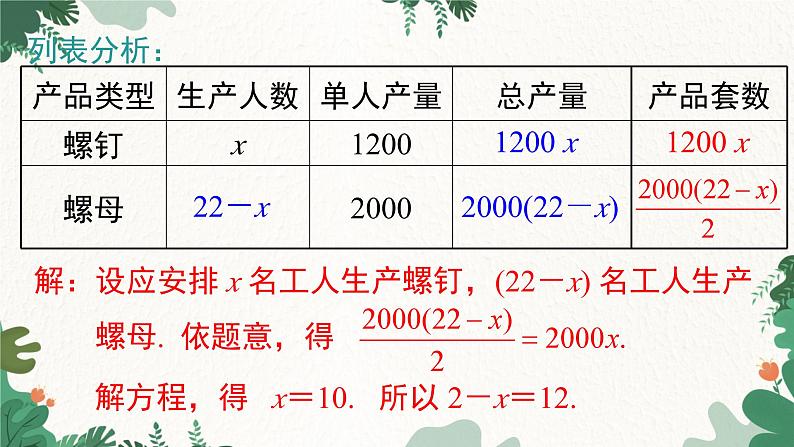
解：设应安排 x 名工人生产螺钉，(22－x) 名工人生 产螺母. 依题意，得 2000(22－x)＝2×1200x . 解方程，得 x＝10. 所以 22－x＝12. 答：应安排 10 名工人生产螺钉，12 名工人生产 螺母.
解：设应安排 x 名工人生产螺钉，(22－x) 名工人生产 螺母. 依题意，得
解方程，得 x＝10. 所以 2－x＝12.
生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系，建立方程.解决配套问题的思路：1. 利用配套问题中物品之间具有的数量关系作为列方程的依据；2. 利用配套问题中的套数不变作为列方程的依据.
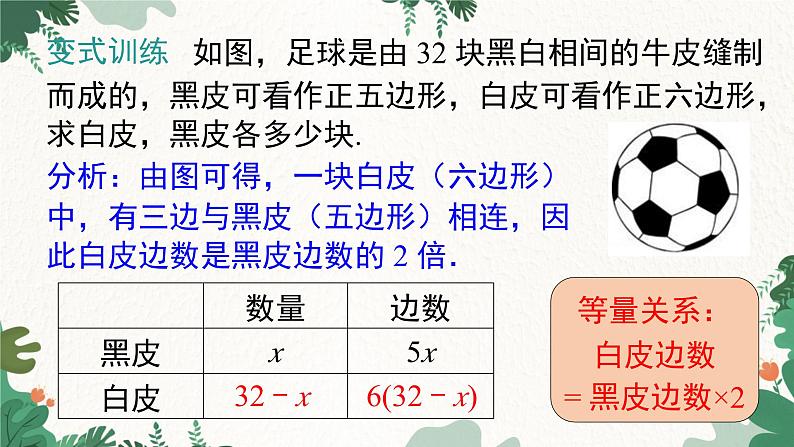
如图，足球是由 32 块黑白相间的牛皮缝制而成的，黑皮可看作正五边形，白皮可看作正六边形，求白皮，黑皮各多少块.
分析：由图可得，一块白皮（六边形）中，有三边与黑皮（五边形）相连，因此白皮边数是黑皮边数的 2 倍．
等量关系：白皮边数= 黑皮边数×2
解：设足球上黑皮有 x 块，则白皮为 (32 - x) 块，五边形的边数共有 5x 条，六边形边数有 6(32 - x) 条.依题意，得 2×5x = 6(32 - x).解得 x = 12. 则 32 - x = 20.答：白皮 20 块，黑皮 12 块.
一套仪器由一个 A 部件和三个 B 部件构成. 用1 立方米钢材可做 40 个 A 部件或 240 个 B 部件.现要用 6 立方米钢材制作这种仪器，应用多少钢材做 A 部件，多少钢材做 B 部件，才能恰好配成整数套这种仪器？共配成多少套？ 分析：由题意知 B 部件的数量是 A 部件数量的 3 倍，可根据这一等量关系得到方程.
解：设应用 x 立方米钢材做 A 部件，则应用 (6－x) 立方米钢材做 B 部件. 根据题意，列方程得 3×40x = (6－x)×240. 解得 x = 4. 则 6－x = 2. 共配成仪器 4×40 = 160 (套).
答：应用 4 立方米钢材做 A 部件， 2 立方米钢材做 B 部件，共配成仪器 160 套.
如果把总工作量设为 1，那么人均效率 (一个人 1 h 完成的工作量) 为 ，
x 人先做 4 h 完成的工作量为 ，增加 2 人后再做 8 h 完成的工作量为 ，
这两个工作量之和等于 .
例2 整理一批图书，由一个人做要 40 h 完成. 现计划由一部分人先做 4 h，然后增加 2 人与他们一起做 8 h，完成这项工作. 假设这些人的工作效率相同，具体应先安排多少人工作？
如果设先安排 x 人做 4 h，你能列出方程吗？
解：设先安排 x 人做 4 h，根据题意得等量关系： 可列方程 解方程，得 x＝2. 答：应先安排 2 人做 4 小时.
加工某种工件，甲单独作要 20 天完成，乙只要 10 天就能完成任务，现在要求二人在 12 天内完成任务．问乙需工作几天后甲再继续加工才可正好按期完成任务？
解：设乙需工作 x 天后甲再继续加工才可正好按期完成任务，则甲做了 (12 - x) 天.
解得 x = 8.
答：乙需工作 8 天后甲再继续加工才可正好按期完成任务.
想一想：若要求二人在 8 天内完成任务，乙先加工几天后，甲加入合作加工，恰好能如期完成任务？
解：设甲加工 x 天，两人如期完成任务，则在甲加入之前，乙先工作了 (8 - x) 天.
解得 x = 4. 则 8 - x = 4.
答：乙需加工 4 天后，甲加入合作加工才可正好按期完成任务.
解决工程问题的基本思路：1. 三个基本量：工作量、工作效率、工作时间. 它们之间的关系是：工作量 = 工作效率×工作时间.2. 相等关系：工作总量 = 各部分工作量之和. (1) 按工作时间，工作总量 = 各时间段的工作量之和； (2) 按工作者，工作总量 = 各工作者的工作量之和.3. 通常在没有具体数值的情况下，把工作总量看作 1.
一条地下管线由甲工程队单独铺设需要 12 天，由乙工程队单独铺设需要 24 天. 如果由这两个工程队从两端同时施工，要多少天可以铺好这条管线？
解方程，得 x = 8.
答：要 8 天可以铺好这条管线.
解：设要 x 天可以铺好这条管线，由题意得
1. 某人一天能加工甲种零件 50 个或加工乙种零件 20 个，1 个甲种零件与 2 个乙种零件配成一套，30 天制作最多的成套产品，若设 x 天制作甲种零件， 则可列方程为 .
2×50x = 20(30－x)
2. 一项工作，甲独做需 18 天，乙独做需 24 天，如果 两人合做 8 天后，余下的工作再由甲独做 x 天完成， 那么所列方程为 .
3. 某家具厂生产一种方桌，1 m3 的木材可做 50 个桌面 或 300 条桌腿，现有 10 m3 的木材，怎样分配生产桌 面和桌腿使用的木材，才能使桌面、桌腿刚好配套？ 共可生产多少张方桌 (1 张方桌有 1 个桌面,4 条桌腿)?
解：设用 x m3 的木材做桌面，则用 (10－x) m3 的木材 做桌腿. 根据题意，得 4×50x = 300(10－x)， 解得 x = 6. 所以 10－x = 4，50×6 = 300. 答：用 6 m3 的木材做桌面，4 m3 的木材做桌腿， 可做 300 张方桌.
4. 一件工作，甲单独做 20 小时完成，乙单独做 12 小时 完成，现在先由甲单独做 4 小时，剩下的部分由甲、 乙合做. 剩下的部分需要几小时完成？
解：设剩下的部分需要 x 小时完成，根据题意得： 解得 x = 6. 答：剩下的部分需要 6 小时完成.
5. 一个道路工程，甲队单独施工 9 天完成，乙队单独 做 24 天完成．现在甲乙两队共同施工 3 天，因甲 另有任务，剩下的工程由乙队完成，问乙队还需几 天才能完成？
解：设乙队还需 x 天才能完成，由题意得 解得 x = 13. 答：乙队还需 13 天才能完成.
用一元一次方程解决实际问题的基本过程如下：
一元一次方程的解(x = a)