新高考数学一轮复习基础巩固4.1 等差数列（精讲）（含解析）

这是一份新高考数学一轮复习基础巩固4.1 等差数列（精讲）（含解析），共16页。试卷主要包含了等差数列基本量的计算，等差中项，前n项和的性质，等差数列定义及其运用，等差数列的实际应用等内容，欢迎下载使用。
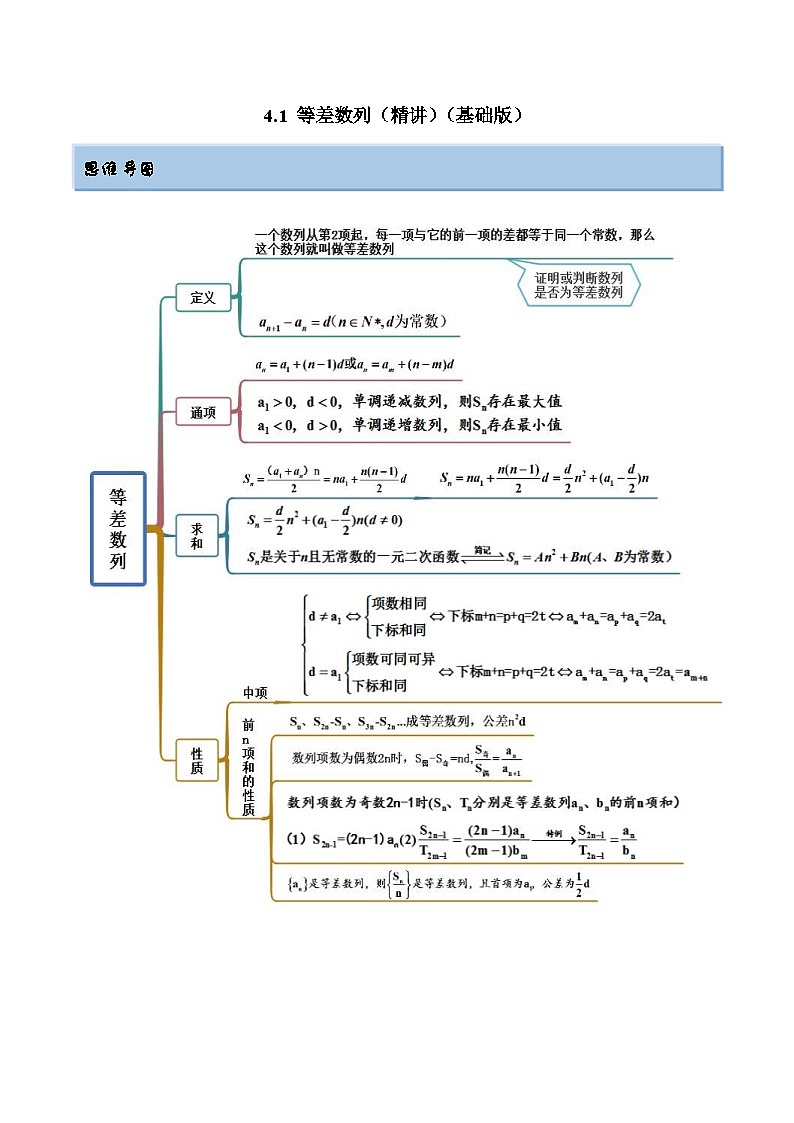
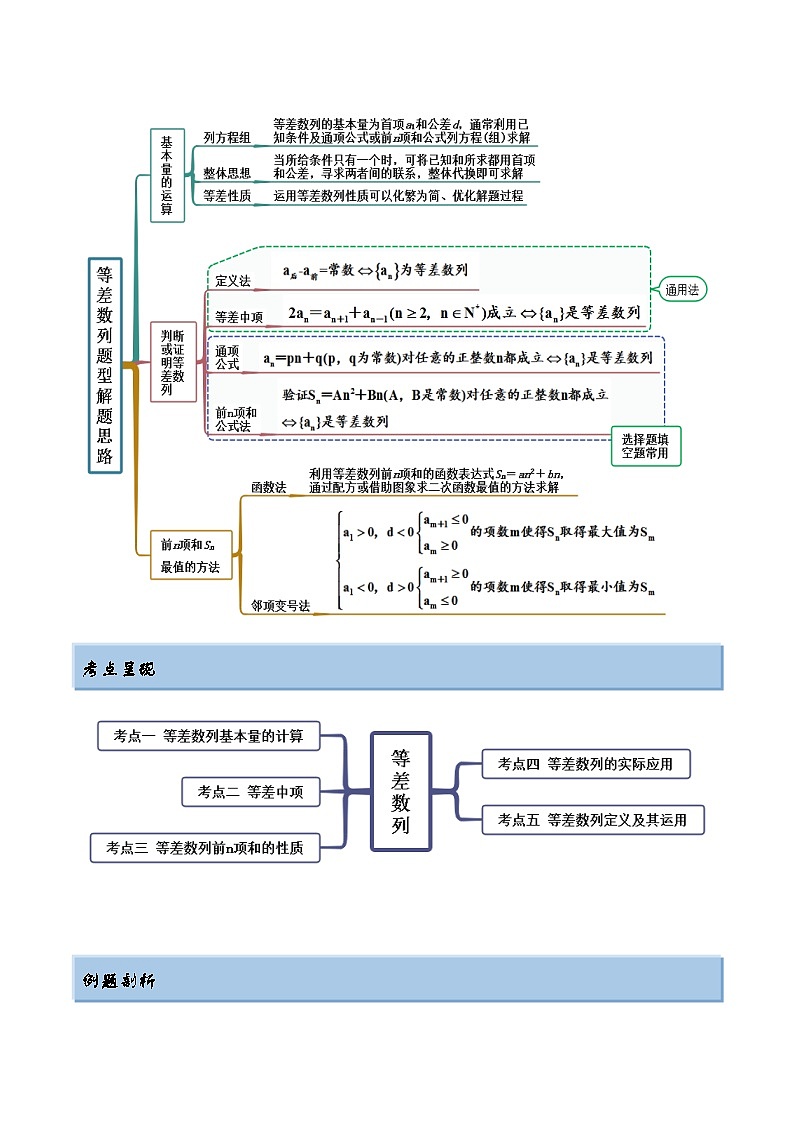
4.1 等差数列（精讲）（基础版）   考点一 等差数列基本量的计算【例1】（2022·福建三明）已知等差数列{}的前n项和为，且，，则＝（       ）A．6 B．10 C．12 D．20【答案】B【解析】因为，，所以解得，所以，故选：B【一隅三反】1．（2022·陕西汉中）已知等差数列的前项和为，，，则等差数列的公差是（       ）A． B． C． D．【答案】D【解析】设等差数列的公差为，由题意可得，解得.故选：D.2．（2022·内蒙古呼和浩特）已知在等差数列中，，则（       ）A．30 B．39 C．42 D．78【答案】B【解析】设等差数列的首项为 ，公差为 ，则 ，解得 ，故，故选：B3．（2022·陕西·西安工业大学附中）设等差数列的前项和为，若，，则（       ）A．20 B．23 C．24 D．28【答案】D【解析】因为是等差数列，所以，又，所以公差为，，故选：D.考点二 等差中项【例2-1】（2022·北京通州·一模）设等差数列的前n项和为，若，则（        ）A．60 B．70 C．120 D．140【答案】B【解析】在等差数列中，，则 ，故，选：B【例2-2】（2022·浙江杭州·二模）设等差数列的前n项和为，若，则（　　）A．12 B．15 C．18 D．21【答案】C【解析】由等差中项的性质得 ， ，即 ， ，故选：C.【例2-3】（2022·安徽滁州）已知是公差不为零的等差数列，若，则（       ）A．7 B．8 C．9 D．10【答案】A【解析】由等差数列的性质得，所以,即故选:A【一隅三反】1．（2022·河北石家庄·二模）等差数列的前n项和记为，若，则（       ）A．3033 B．4044 C．6066 D．8088【答案】C【解析】由等差数列知，，所以，故选：C2．（2022·河南平顶山）已知为正项等差数列的前n项和，若，则（       ）A．22 B．20 C．16 D．11【答案】A【解析】由题意设正项等差数列的首项为 ，公差为 故由得： ，即，故，故选：A3．（2022·全国·高三专题练习）已知数列满足且，则（       ）A．-3 B．3 C． D．【答案】B【解析】,∴数列是以2为公差的等差数列，，，，，故选：B.考点三 前n项和的性质【例3-1】（2022·北京石景山）记为等差数列的前项和，若，，则（       ）A．36 B．45 C．63 D．75【答案】B【解析】因为为等差数列的前项和，所以成等差数列，即成等差数列，所以，解得，故选：B.【例3-2】（1）（2022·江西·临川一中）已知数列和都是等差数列，且其前n项和分别为和，若，则（       ）A． B． C． D．（2）（2022·四川师范大学附属中学二模（理））设等差数列，的前n项和分别是，，若，则（       ）A．             B．              C．                D．3【答案】（1）B（2）B【解析】（1）对于等差数列的前n项和满足，知道，故.故选：B.（2）由等差数列的前项和公式满足形式，设，则，故.故选：B.【例3-3】（2022·全国·高三专题练习）等差数列的前项和为，若且，则(       )A． B．C． D．【答案】A【解析】设的公差为d，∵∴，即{}为等差数列，公差为，由知，故故选：A﹒【例3-4】（1）（2022·内蒙古赤峰）已知等差数列的前n项和为，若，，则取最大值时正整数n的值为（       ）A．9 B．10 C．11 D．12（2）（2022·重庆·二模）（多选）设等差数列前项和为，公差，若，则下列结论中正确的有（       ）A． B．当时，取得最小值C． D．当时，的最小值为29【答案】（1）B（2）ABC【解析】（1）设公差为，有，解得，，有，当，可得，可知当时，，故取最大值时正整数n的值为10．故选：B（2）根据题意，由.故A正确；因为，故当时，，，当时，，当或时，取得最小值，故B正确；由于，故C正确；因为，，所以由，可得：，因此n的最小值为，故D错误.故选：ABC【一隅三反】1．（2022·全国·高三专题练习）设等差数列的前项和为，若，，则等于（       ）A．-3 B．-12 C．-21 D．-30【答案】D【解析】由等差数列的性质知：成等差数列，∴，则，可得.同理：，即，得.故选：D2．（2022·全国·高三）若等差数列和的前n项的和分别是和，且，则（       ）A． B． C． D．【答案】B【解析】因为等差数列和的前n项的和分别是和，且，所以.故选：B.3．（2022·全国·高三专题练习）设等差数列与等差数列的前n项和分别为，，若对任意自然数n都有，则的值为（       ）A． B． C． D．【答案】C【解析】由题意，.故选：C.4．（2022·全国·高三专题练习）在等差数列中，，其前项和为，若，则等于（       ）A． B． C． D．【答案】B【解析】数列为等差数列，数列为等差数列，设其公差为，又，解得：，又，，.选：B.5．（2022·全国·高三专题练习）（多选）等差数列{an}的前n项和记为Sn，若a1>0，S10＝S20，则（       ）A．d<0          B．a16<0              C．Sn≤S15                  D．当且仅当n≥32时，Sn<0【答案】ABC【解析】对于A，设等差数列{an}的公差为d，由S10＝S20，得10a1＋d＝20a1＋d，化简得a1＝d.因为a1>0，所以d<0，故A正确；对于B，因为a16＝a1＋15d＝d＋15d＝d，又d<0，所以a16<0，故B正确；对于C，因为a15＝a1＋14d＝d＋14d＝－d>0，a16<0，所以S15最大，即Sn≤S15，故C正确；对于D，，若Sn<0，又d<0，则n>30，故当且仅当n≥31时，Sn<0，故D错误．故选：ABC6．（2022·浙江省浦江中学高三期末）设等差数列的公差为d，其前n项和为，且，，则使得的正整数n的最小值为（       ）A．16 B．17 C．18 D．19【答案】D【解析】由，得，因为是等差数列，所以，，，，，，所以，使得的正整数n的最小值为.故选: D.考点四 等差数列定义及其运用【例4-1】（2022·全国·高三专题练习）（多选）下列数列是等差数列的是（       ）A．0，0，0，0，0，… B．1，l，111，111l，…C．－5，－3，－1，1，3，… D．1，2，3，5，8，…【答案】AC【解析】根据等差数列的定义可知A，C中的数列是等差数列，而BD中，从第2项起，后一项与前一项的差不是同一个常数，故选：AC．【例4-2】（2022·全国·高三专题练习）在数列中，有,证明：数列为等差数列，并求其通项公式.【答案】证明见解析，【解析】设数列的前n项和为，则已知转化为当时,，上述两式相减并整理，得.又因为时，，适合上式，所以.从而得到，所以，所以数列为等差数列，且其通项公式为.【例4-3】（2022·四川·泸县五中模拟预测（理））下列选项中，为“数列是等差数列”的一个充分不必要条件的是（       ）A． B．C．通项公式 D．【答案】C【解析】对于A：数列是等差数列，∴A选项为“数列是等差数列”的一个充要条件，故A错误；对于B：易知B选项为“数列是等差数列”的一个既不充分也不必要条件，故B错误；对于C：∵，∴，∴，∴数列是等差数列，反之若为等差数列，则，此时不一定为2，所以必要性不成立，∴C选项为“数列是等差数列”的一个充分不必要条件，故C正确；对于D：若数列是等差数列，则，∴成立，反之当，，，时，满足，但不是等差数列，∴D选项为“数列是等差数列”的一个必要不充分条件，故D错误．故选：C．【例4-4】（2022·全国·高三专题练习）已知不全相等的实数，，成等比数列，则一定不可能是等差数列的为（       ）A．，， B．，， C．，， D．，，【答案】D【解析】因为不全相等的实数，，成等比数列，所以该等比数列的公比，显然有，，A：若，，成等差数列，显然成立，即，化简为，解得，或（舍去），所以假设成立，故，，有可能是等差数列；B：若，，成等差数列，显然成立，即，化简为：，解得：，显然或，所以假设成立，故，，有可能成等差数列；C：若，，成等差数列，显然，即，化简为：，解得，因为，所以，因此假设成立，故，，有可能 成等差数列；D：若，，成等差数列，显然，即，化简为：，解得，而，因此假设不成立，故，，一定不可能成等差数列，故选：D【一隅三反】1．（2022·全国·课时练习）（多选）若是等差数列，则下列数列为等差数列的有（       ）A． B． C． D．【答案】ACD【解析】设等差数列的公差为d，当时，.对于A，，为常数， 因此是等差数列；故A正确对于B，，不为常数，因此不是等差数列；故B错误对于C，，为常数，因此是等差数列；故C正确对于D，，为常数，因此是等差数列.故D正确故选：ACD.2．（2022·全国·高二课时练习）（多选）在数列中，，且对任意大于的正整数，点在直线上，则（       ）A．数列是等差数列                              B．数列是等差数列C．数列的通项公式为                      D．数列的通项公式为【答案】BD【解析】点在直线上，，数列是以为首项，为公差的等差数列，B正确；，D正确；，C错误；，不是等差数列，A错误.故选：BD.3．（2022·全国·课时练习）（多选）下列数列中是等差数列的是（       ）A．，a，                              B．2，4，6，8，…，，C．，，，             D．【答案】ABD【解析】对于A选项，由于，故是等差数列，正确；对于B选项，2，4，6，8，…，，中，，是等差数列，正确；对于C选项，因为，，又，即第3项与第2项的差不等于第2项与第1项的差，故不是等差数列；对于D选项，由得，满足等差数列定义.故选：ABD.4．（2022·全国·高三专题练习）已知数列中，，当n≥2时，.求证:数列是等差数列.【答案】证明见解析；【解析】当n≥2时，，因，显然，否则，由此可得，矛盾， 两边同时除以，得，而=1，所以数列是以1为首项，1为公差的等差数列.考点五 等差数列的实际应用【例5】（2022·海南·文昌中学高三阶段练习）《周髀算经》是中国古代天文学与数学著作，其中有关于24节气的描述，将一年分为24个节气，如图所示，已知晷长指太阳照射物体影子的长度，相邻两个节气的晷长变化量相同（即每两个相邻节气晷长增加或减小量相同，其中冬至晷长最长，夏至晷长最短，从夏至到冬至晷长逐渐变大，从冬至到夏至晷长逐渐变小.周而复始，已知冬至晷长为13.5尺，芒种晷长为2.5尺，则一年中秋分这个节气的晷长为（       ）A．6.5尺 B．7.5尺 C．8.5尺 D．95尺【答案】B【解析】冬至到夏至晷长记为数列，数列为等差数列，公差，冬至晷长，若芒种晷长所以，所以夏至晷长夏至到冬至晷长记为数列{}，数列{}为等差数列，公差，夏至晷长秋分这个节气的晷长故选：B【一隅三反】1.（2022·江苏南通·模拟预测）《张邱建算经》曾有类似记载：“今有女子善织布，逐日织布同数递增（即每天增加的数量相同）".若该女子第一天织布两尺，前二十日共织布六十尺，则该女子第二十日织布（       ）A．三尺 B．四尺 C．五尺 D．六尺【答案】B【解析】用表示该女子第天织布尺寸，则，，由，得，．故选：B．2．（2022·天津市西青区杨柳青第一中学高三阶段练习）北京天坛圜丘坛的地面由石板铺成，最中间的是圆形的天心石，围绕天心石的是9圈扇环形的石板，从内到外各圈的石板数依次为，，，…，，设数列为等差数列，它的前n项和为，且，，则（       ）A．189 B．252C．324 D．405【答案】D【解析】设等差数列的公差为，由，，得，解得：，所以.故选：D.3．（2022·黑龙江·哈九中三模（理））南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列，如数列1，3，6，10，前后两项之差得到新数列2，3，4，新数列2，3，4为等差数列，这样的数列称为二阶等差数列．对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”．现有高阶等差数列，其前7项分别为3，4，6，9，13，18，24，则该数列的第17项为（       ）A．139 B．160 C．174 D．188【答案】A【解析】由题意可知，设该数列为，数列的前7项分别为3，4，6，9，13，18，24，则数列满足，，.所以.故选：A.