新高考数学一轮复习基础巩固10.3 椭圆（精讲）（含解析）

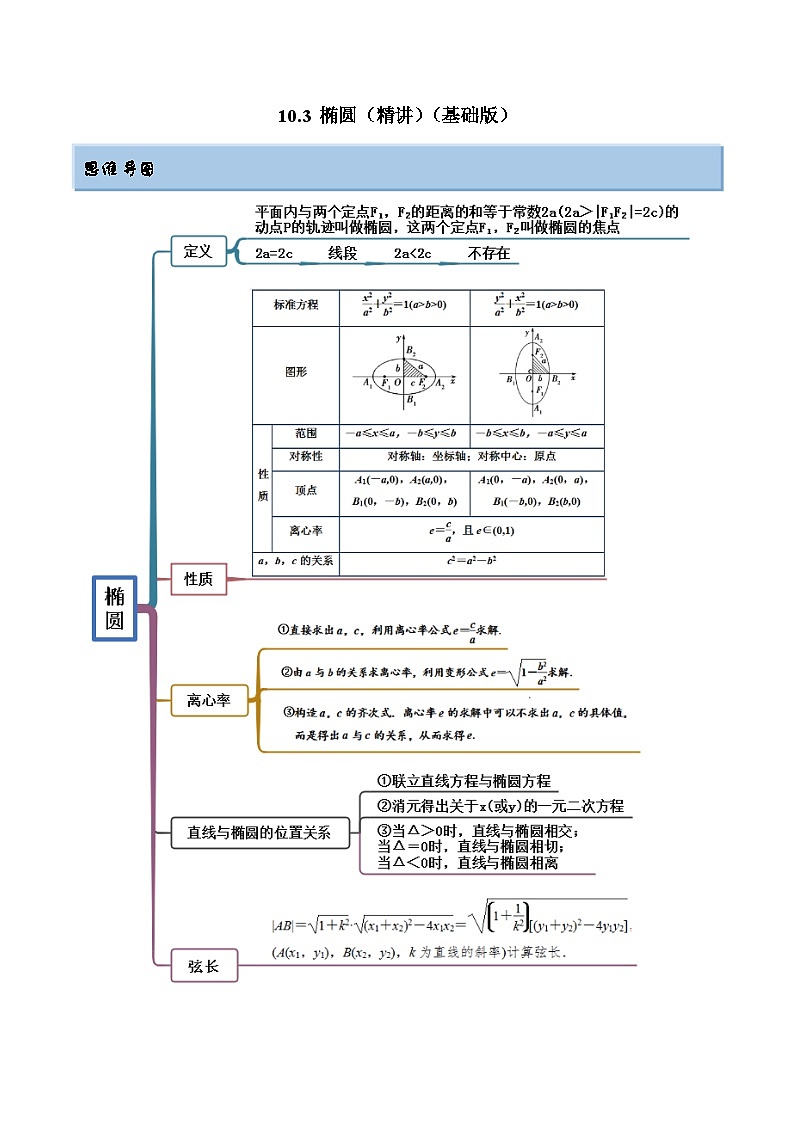
这是一份新高考数学一轮复习基础巩固10.3 椭圆（精讲）（含解析），共14页。试卷主要包含了椭圆的定义及应用，椭圆的离心率，椭圆的标准方程，直线与椭圆的位置关系，弦长等内容，欢迎下载使用。
10.3 椭圆（精讲）（基础版）考点一 椭圆的定义及应用【例1-1】（2022·日照模拟）已知曲线 ，则“ ”是“曲线C是椭圆”的(　　)  A．充要条件 B．充分不必要条件C．必要不充分条件 D．既不充分也不必要条件【答案】C【解析】若曲线 表示椭圆，则 ， 故“ ”是“曲线C是椭圆”的必要不充分条件．故答案为：C．【例1-2】（2022滁州）已知椭圆的焦点为、，P为椭圆上的一点，若，则的面积为（　　）A．3 B．9 C． D．【答案】C【解析】根据椭圆的定义有，①根据余弦定理得，②结合①②解得，所以的面积。故答案为：C【例1-3】（2022·邵阳模拟）已知椭圆C：的左､右焦点分别为，，点P在椭圆C上，的周长为16，则　     　.【答案】5【解析】设焦距为2c，因为的周长为16，所以   ，化简得   ①.又   ，所以   ，可得   ②，由①②，解得   .故答案为：5【一隅三反】1．（2021湖南月考）若椭圆上一点A到焦点的距离为3，则点A到焦点的距离为（　　）A．6 B．5 C．4 D．3【答案】B【解析】由椭圆的定义知，。 故选：B2．（2022高三下·广东月考）设P为椭圆上一点，分别是C的左，右焦点．若，则（　　）A． B． C． D．【答案】C【解析】椭圆的长半轴长为3，  由椭圆的定义可知   ，由   ，可得   ．故答案为：C3．（2022洛阳月考）若方程表示椭圆，复数z满足，则复数z的共轭复数是（　　）A． B． C． D．【答案】A【解析】因为方程表示椭圆，所以解得，因为，所以，所以，所以，所以，所以复数z的共轭复数为。故答案为：A．4．（2021定州期末）设P为椭圆C：上一点，，分别为左、右焦点，且，则（　　）A． B． C． D．【答案】B【解析】根据P为椭圆C：上一点， 则有，又，所以，故答案为：B.4．（2022·江西模拟）“ ， ”是“方程 表示的曲线为椭圆”的（　　）  A．充要条件 B．必要不充分条件C．充分不必要条件 D．既不充分也不必要条件【答案】D【解析】[解法一]方程 即方程 ，表示椭圆的充分必要条件是 ，显然“ ， ”是“ ”既不充分也不必要条件，故“ ， ”是“方程 表示的曲线为椭圆”的既不充分也不必要条件，[解法二]当 时，满足“ ， ”，此时题中方程可化为： ，表示的曲线是圆而不是椭圆，当 时，不满足“ ， ”，只是题中方程可化为： ，表示中心在原点，半长轴为1，半短轴为 的椭圆，故：“ ， ”是“方程 表示的曲线为椭圆”的既不充分也不必要条件，故答案为：D考点二 椭圆的离心率【例2-1】（202深圳月考）已知 ， 是椭圆的两个焦点，过 且与椭圆长轴垂直的直线交椭圆于 ， 两点，若 是正三角形，则这个椭圆的离心率是（　　）  A． B． C． D．【答案】B【解析】∵ 是正三角形，∴，
∴∴. 故答案为：B.
【例2-2】（2022延庆期末）椭圆的左右焦点分别为，是上一点， 轴，，则椭圆的离心率等于（　　）A． B． C． D．【答案】A【解析】令椭圆的半焦距为c，因是上一点， 轴，， 在中，，，由椭圆定义知，则，所以椭圆的离心率等于.答案为：A【一隅三反】1．（2021昌吉期中）已知，是椭圆的两个焦点，是上的一点，若，且，则的离心率为（　　）A． B． C． D．【答案】D【解析】在中，设，则，又由椭圆定义可知则离心率。故答案为：D.2．（2022河南月考）已知椭圆：经过点，且的离心率为，则的方程是（　　）A． B． C． D．【答案】A【解析】依题意可得，解得， 故椭圆的标准方程是。故答案为：A.3．（2022·湖南邵阳）椭圆方程为椭圆内有一点，以这一点为中点的弦所在的直线方程为，则椭圆的离心率为______．【答案】【解析】设直线与椭圆交于，则.因为AB中点,则.又，相减得：.所以所以所以，所以，即离心率.故答案为：.考点三 椭圆的标准方程【例3】（2022石景山期末）已知椭圆的焦点为，．过点的直线与交于，两点．若的周长为8，则椭圆的标准方程为（　　）A． B． C． D．【答案】C【解析】因为椭圆的焦点为，，所以； 又过点的直线与交于，两点，的周长为8，则根据椭圆定义可得，，解得，因此，所以椭圆的标准方程为.故答案为：C.【一隅三反】1．（2022长沙期末）在平面直角坐标系中，椭圆的中心在原点，焦点在轴上，离心率为 ，过的直线交椭圆于两点，且的周长为16，则椭圆的方程为（　　）A． B． C． D．【答案】D【解析】设椭圆方程为由椭圆定义知：的周长为即，解得：椭圆的方程为故答案为：D
2．（2022大连期末）阿基米德出生于希腊西西里岛叙拉古，享有“力学之父”的美称，和高斯、牛顿并列为世界三大数学家，他利用“逼近法”得到椭圆的面积等于圆周率、椭圆的半长轴长、椭圆的半短轴长三者的乘积.已知椭圆C：的面积为，左右焦点分别为，，M为椭圆C上一点，且的周长为16，则椭圆C的方程为（　　）A． B． C． D．【答案】D【解析】由题意可知，解得，即椭圆C的方程为.故答案为：D3．（2022·静安模拟）以坐标原点为中心的椭圆的长轴长等于8，且以抛物线的焦点为一个焦点，则该椭圆的标准方程是（　　）A． B． C． D．【答案】D【解析】由抛物线方程知，抛物线焦点坐标为，所以椭圆中，又因为，，所以，焦点在轴， 所以椭圆方程为。故答案为：D．4．（2022齐齐哈尔期末）如图所示，已知是椭圆的左､右焦点，为椭圆的上顶点，在轴上，，且是的中点，为坐标原点，若点到直线的距离为3，则椭圆的方程为（　　）A． B． C． D．【答案】D【解析】且，则△是等边三角形， 设，则①，∴直线的方程为，即，∴到直线的距离为②，又③，联立①②③，解得，，故椭圆的标准方程为。故答案为：D.考点四 直线与椭圆的位置关系【例4-1】（2023·全国·高三专题练习）直线与椭圆的位置关系是（       ）A．相交 B．相切 C．相离 D．不确定【答案】A【解析】，在椭圆内，恒过点，直线与椭圆相交.故选：A.【例4-2】（2022·山西）直线与椭圆有且只有一个交点，则的值是(       )A． B． C． D．【答案】C【解析】由得，，由题意知，解得，故选：C．【一隅三反】1．（2022·辽宁）已知直线l：，曲线C：，则直线l与曲线C的位置关系是（       ）A．相离 B．相切 C．相交 D．无法确定【答案】C【解析】由直线l：，得直线l过定点，因为，所以该点在曲线C：内部.所以直线l与曲线C相交.故选：C.2．（2022·全国·高三专题练习）直线和曲线的位置关系为_____.【答案】相交【解析】曲线为：可得直线恒过，由知定点在椭圆内部，所以直线与椭圆的位置关系为相交.故答案为：相交.3．（2022·全国·专题练习）不论为何值，直线与椭圆有公共点，则实数的范围是__.【答案】【解析】方法一： 把直线代入椭圆1，化为．其中．(注意这个坑)，直线与椭圆1有公共点，恒成立，化简为．上式对于任意实数都成立，，解得．实数的范围是． 方法二：因为直线恒过定点所以代入得即因为是椭圆，所以故的取值范围是．故答案为：考点五 弦长【例5-1】（2022·吉林省实验中学）已知斜率为1的直线l过椭圆的右焦点，交椭圆于A，B两点，则弦AB的长为（       ）A． B． C． D．【答案】C【解析】由椭圆知，，所以，所以右焦点坐标为，则直线的方程为，设，联立，消y得，，则，所以.即弦AB长为.故选：C.【例5-2】（2022·全国·课时练习）已知双曲线方程，则以为中点的弦所在直线的方程是（       ）A． B． C． D．【答案】B【解析】设直线交双曲线于点、，则，由已知得，两式作差得，所以，，即直线的斜率为，故直线的斜率为，即.经检验满足题意故选：B.【一隅三反】1．（2023·全国·高三专题练习）已知椭圆，则以点为中点的弦所在的直线方程为（　　）A． B．C． D．【答案】C【解析】设弦的两个端点分别为，，则，①﹣②得：，即，所以．故以点为中点的弦所在的直线方程为y，整理得：.故选：C.2．（2022·福建·厦门双十中学 ）已知直线，椭圆．若直线l与椭圆C交于A，B两点，则线段AB的中点的坐标为（       ）A． B．C． D．【答案】B【解析】由题意知，，消去y，得，则，，所以A、B两点中点的横坐标为：，所以中点的纵坐标为：，即线段AB的中点的坐标为.故选：B3．（2022·云南）椭圆的中心在坐标原点，焦点在轴上，椭圆经过点且长轴长为.(1)求椭圆的标准方程；(2)过点且斜率为1的直线与椭圆交于，两点，求弦长.【答案】(1)(2)【解析】（1）由题意设椭圆的方程为，因为椭圆经过点且长轴长为，所以，所以椭圆方程为，（2）因为直线过点且斜率为1，所以直线的方程为，设，将代入，得，整理得，所以，所以.