高中数学湘教版（2019）选择性必修 第一册第3章 圆锥曲线与方程3.3 抛物线作业ppt课件

这是一份高中数学湘教版（2019）选择性必修 第一册第3章 圆锥曲线与方程3.3 抛物线作业ppt课件，共26页。PPT课件主要包含了x2-4y，故选D，ABC等内容，欢迎下载使用。
1.以x轴为对称轴,通径长为8,顶点在坐标原点的抛物线的标准方程是(　　)A.y2=8x或x2=8yB.y2=-8x或x2=-8yC.y2=8x或y2=-8xD.x2=8y或x2=-8y
解析 当抛物线的焦点在x轴的正半轴上时,设抛物线的标准方程为y2=2px(p>0),可得2p=8,解得p=4,所以抛物线的标准方程为y2=8x;当抛物线的焦点在x轴的负半轴上时,设抛物线的标准方程为y2=-2px(p>0),可得2p=8,解得p=4,所以抛物线的标准方程为y2=-8x.所以所求抛物线的标准方程为y2=±8x.故选C.
2.已知F为抛物线C:x2=4y的焦点,直线l与C交于A,B两点,若AB中点的纵坐标为3,则|AF|+|BF|的值(　　)A.等于8B.等于7C.等于5D.随A,B两点坐标变化而变化
解析 设A(x1,y1),B(x2,y2),则|AF|+|BF|=y1+y2+p=6+2=8,故选A.
3.抛物线C:y2=2px(p>0)上一点(1,y0)到其焦点的距离为3,则抛物线C的标准方程为(　　)A.y2=4xB.y2=8xC.y2=12xD.y2=16x
解析 抛物线C:y2=2px(p>0)的准线方程为x= ,由抛物线的定义以及抛物线上一点(1,y0)到其焦点的距离为3,可得1-( )=3,解得p=4,所以抛物线的标准方程为y2=8x.故选B.
4.已知点(x,y)在抛物线y2=4x上,则z=x2+ y2+3的最小值是(　　)A.2B.3C.4D.0
解析 因为点(x,y)在抛物线y2=4x上,所以x≥0.
5.(多选题)平面内到定点F(0,1)和到定直线l:y=-1的距离相等的动点的轨迹为曲线C,则(　　)A.曲线C的标准方程为x2=4yB.曲线C关于y轴对称C.当点P(x,y)在曲线C上时,y≥2D.当点P在曲线C上时,点P到直线l的距离d≥2
解析 由抛物线定义可知曲线C是以F为焦点,直线l为准线的抛物线,其标准方程为x2=4y,曲线关于y轴对称,故A正确,B正确;由x2=4y知y≥0,故C错误;点P到直线l的距离d≥1,故D错误.故选AB.
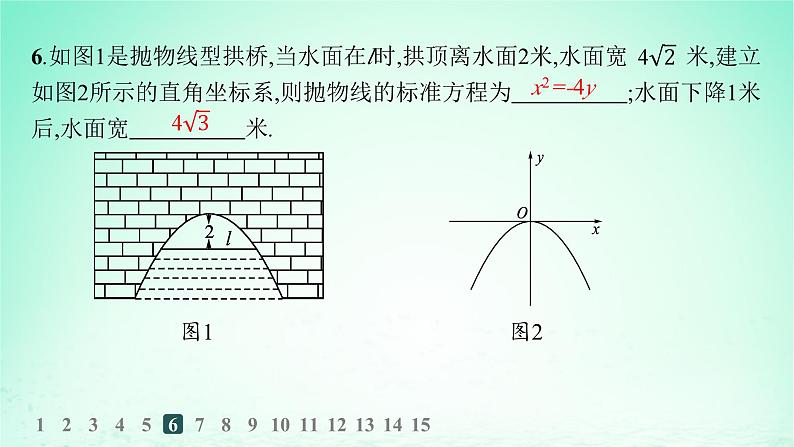
6.如图1是抛物线型拱桥,当水面在l时,拱顶离水面2米,水面宽 米,建立如图2所示的直角坐标系,则抛物线的标准方程为　　　　　;水面下降1米后,水面宽　　　　　米. 
7.已知抛物线的焦点F在x轴的正半轴上,直线l过点F且垂直于x轴,l与抛物线交于A,B两点,O为坐标原点.若△OAB的面积等于4,则抛物线的标准方程为　　 　　　. 
8.已知抛物线C:y2=2px(p>0)的焦点为F,且抛物线C与y=2x的一个交点是M(m,2).(1)求抛物线C的标准方程;(2)若直线l:y=x+n(n≠0)与抛物线C交于A,B两点,且OA⊥OB(O为坐标原点),求n的值.
9.已知直线l过抛物线C:y2=x的焦点,并交抛物线C于A,B两点,|AB|=2,则弦AB的中点G的横坐标是(　　)
解析 如图所示,由题意可得抛物线的准线m的方程为x= .过点G向准线m作垂线,垂足为D,过A,B分别向准线m作垂线,垂足为A',B',则|AA'|+|BB'|=|AB|=2.因为弦AB的中点为G,
10. 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,准线与对称轴交于点M.若|BC|=2|BF|,且|AF|=3,则此抛物线的标准方程为(　　)
解析 由抛物线定义,|BF|等于点B到准线的距离,因为|BC|=2|BF|,所以∠BCM=30°.
故抛物线的标准方程为y2=3x.故选B.
11.已知M是抛物线y2=4x上的一点,F是抛物线的焦点,O为坐标原点,若∠OFM=120°,则|FM|等于(　　)
解析 抛物线y2=4x的焦点坐标为F(1,0),准线方程为x=-1,
12.(多选题)已知抛物线C:y2=2px(p>0)的焦点F到准线的距离是2,过点F的直线l与抛物线交于A,B两点,M为线段AB的中点,O为坐标原点,则下列结论正确的是(　 　)A.C的准线方程为x=-1B.线段AB的长度的最小值为4C.M的坐标可能是(3,2)D.存在直线l,使得OA与OB垂直
解析 由已知可得p=2,所以抛物线的标准方程为y2=4x,则点F(1,0),准线的方程为x=-1,故A正确;当AB⊥x轴时,AB的长度取最小值,令x=1,代入抛物线方程解得y=±2,所以AB的长度的最小值为4,故B正确;设直线l的方程为x=my+1,A(xA,yA),B(xB,yB),M(xM,yM),将x=my+1代入抛物线方程可得y2-4my-4=0,Δ=16(m2+1)>0,则yA+yB=4m,所以xA+xB=m(yA+yB)+2=4m2+2,xM=2m2+1,当m=1时,可得M(3,2),故C正确;
D错误.故选ABC.
13.抛物线x2=y上到直线2x-y-4=0的距离最短的点的坐标是　　　　　. 
当x0=1时,抛物线x2=y上一点到直线2x-y-4=0的距离最短,此时点A的坐标为(1,1).
所以y1+y2=2,从而-3y2+y2=2,故y2=-1,y1=3.
15.已知抛物线E的顶点为坐标原点,对称轴为x轴,且直线y=x+1与E相切.(1)求E的标准方程;(2)设P为E的准线上一点,过P作E的两条切线,切点为A,B,求证:PA⊥PB.
(1)解 依题意可设抛物线的标准方程为y2=2px(p>0),与直线y=x+1联立,可得x2+(2-2p)x+1=0,由Δ=(2-2p)2-4=0,解得p=2(p=0舍去).所以抛物线的标准方程为y2=4x.