数学选择性必修 第一册第一章　空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.2 空间中的平面与空间向量作业ppt课件

这是一份数学选择性必修 第一册第一章　空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.2 空间中的平面与空间向量作业ppt课件，共39页。PPT课件主要包含了解析∵α∥β，①②③，ABC等内容，欢迎下载使用。
1.[探究点一]若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是(　　)A.(0,1,2)B.(3,6,9)C.(-1,-2,3)D.(3,6,8)
解析 向量(1,2,3)与向量(3,6,9)共线.
2.[探究点二(角度1)]设平面α的法向量为(1,-2,λ),平面β的法向量为(2,μ,4),若α∥β,则λ+μ=(　　)A.2B.4C.-2D.-4
3.[探究点二(角度1)]已知n为平面α的一个法向量,l为一条直线,则“l⊥n”是“l∥α”的(　　)A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
解析 当“l⊥n”时,由于l可能在平面α内,所以无法推出“l∥α”;当“l∥α”时,“l⊥n”.综上所述,“l⊥n”是“l∥α”的必要不充分条件.故选B.
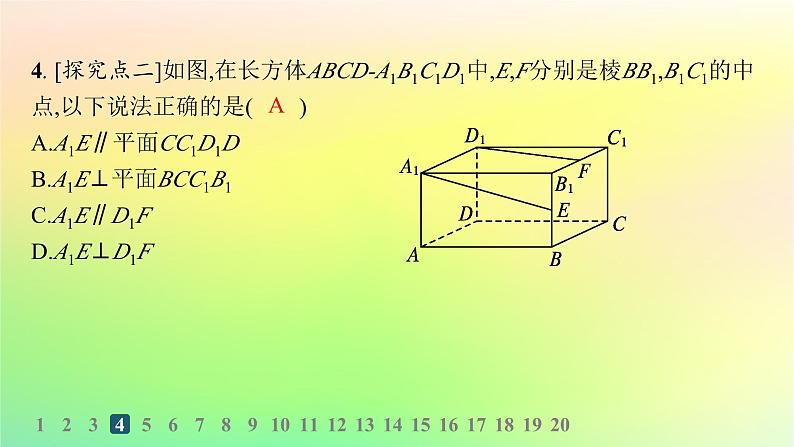
4. [探究点二]如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱BB1,B1C1的中点,以下说法正确的是(　　)A.A1E∥平面CC1D1DB.A1E⊥平面BCC1B1C.A1E∥D1FD.A1E⊥D1F
解析 由长方体的性质有平面ABB1A1∥平面CC1D1D,又A1E⊂平面ABB1A1,所以A1E∥平面CC1D1D,故选项A正确;因为E为棱BB1的中点,且A1B1⊥BB1,所以A1E与BB1不垂直,所以若A1E⊥平面BCC1B1,则A1E⊥BB1,这与A1E和BB1不垂直相矛盾,故选项B错误;
以D为坐标原点,建立如图所示的空间直角坐标系.
所以A1E与D1F不平行,且A1E与D1F不垂直,故选项C,D错误.故选A.
5.[探究点二](多选题)下列利用方向向量、法向量判断线、面位置关系的结论中,正确的是(　　)A.若两条不重合的直线l1,l2的方向向量分别是a=(2,-2,-1),b=(-2,-2,1),则l1∥l2B.若直线l的方向向量是a=(1,1,2),平面α的一个法向量是n=(-2,-2,-4),则l⊥αC.若直线l的方向向量是a=(0,2,0),平面α的一个法向量是n=(-2,0,2),则l∥αD.若两个不同的平面α,β的法向量分别是m=(3,-4,2),n=(-2,0,3),则α⊥β
解析 对于A,因为向量a,b不平行,所以l1,l2不平行,故A不正确;对于B,因为n=-2a,所以a∥n,故B正确;对于C,因为a·n=0×(-2)+2×0+0×2=0,所以a⊥n,所以l∥α或l⊂α,故C不正确;对于D,因为m·n=-6+0+6=0,所以α⊥β,故D正确.故选BD.
6.[探究点二(角度2)]已知直线l与平面α垂直,直线l的一个方向向量u=(1,-3,z),向量v=(3,-2,1)与平面α平行,则z=　　　　. 
解析 题知,u⊥v,∴u·v=3+6+z=0,∴z=-9.
AB∥平面CDE或AB⊂平面CDE
8.[探究点二·2023广东佛山高二阶段练习]若平面α的一个法向量为m=(2,-6,s),平面β的一个法向量为n=(1,t,2),且α∥β,则s-t=　　　　　. 
9.[探究点一]在如图所示的坐标系中,ABCD-A1B1C1D1表示棱长为1的正方体,给出下列结论:①直线DD1的一个方向向量为(0,0,1);②直线BC1的一个方向向量为(0,1,1);③平面ABB1A1的一个法向量为(0,1,0);④平面B1CD的一个法向量为(1,1,1).其中正确的是　　　　.(填序号) 
10. [探究点一]在正方体ABCD-A1B1C1D1中,E,F分别为棱A1D1,A1B1的中点,在如图所示的空间直角坐标系中,求:(1)平面BDD1B1的一个法向量;(2)平面BDEF的一个法向量.
解 设正方体ABCD-A1B1C1D1的棱长为2,则D(0,0,0),B(2,2,0),D1(0,0,2),E(1,0,2).(1)设平面BDD1B1的一个法向量为n=(x1,y1,z1).
令x1=1,则y1=-1,z1=0,∴平面BDD1B1的一个法向量为n=(1,-1,0).
令x2=2,则y2=-2,z2=-1,∴平面BDEF的一个法向量为m=(2,-2,-1).
11.[探究点二(角度1)]如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
又MN⊄平面A1BD,∴MN∥平面A1BD.(方法二)如图,以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,设正方体的棱长为1,则可求得
设平面A1BD的法向量是n=(x,y,z),
取x=1,得y=-1,z=-1.∴n=(1,-1,-1).
又MN⊄平面A1BD,∴MN∥平面A1BD.
12.[探究点二(角度2)]如图,在四棱锥P - ABCD中,PA⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.求证:(1)AE⊥CD;(2)PD⊥平面ABE.
证明 (1)∵AB,AD,AP两两垂直,∴建立如图所示的空间直角坐标系.设PA=AB=BC=1,则P(0,0,1).∵∠ABC=60°,∴△ABC为正三角形.
∴PD⊥AB.又AB∩AE=A,AB⊂平面ABE,AE⊂平面ABE,∴PD⊥平面ABE.
13.已知平面α内两向量a=(1,1,1),b=(0,2,-1),且c=ma+nb+(4,-4,1).若c为平面α的法向量,则m,n的值分别为(　　)A.-1,2B.1,-2C.1,2D.-1,-2
解析 c=ma+nb+(4,-4,1)=(m,m,m)+(0,2n,-n)+(4,-4,1)=(m+4,m+2n-4,m-n+1),由c为平面α的法向量,
14.已知直线l的方向向量为a,且直线l不在平面α内,平面α内两共点向量
解析 A,B,C中均能推出l∥α,或l⊂α,但不能确定一定能表示为l∥α.
15.[2023河南商城高二阶段练习]已知直线l的方向向量是a=(3,2,1),平面α的法向量是u=(-1,2,-1),则l与α的位置关系是(　　)A.l⊥αB.l∥αC.l与α相交但不垂直D.l∥α或l⊂α
解析 ∵a·u=-3+4-1=0,∴a⊥u,∴l∥α或l⊂α.故选D.
16.[2023广东佛山高二阶段练习]已知两个不重合的平面α与平面ABC,若平
A.平面α∥平面ABCB.平面α⊥平面ABCC.平面α,平面ABC相交但不垂直D.以上均有可能
∴n1也为平面ABC的一个法向量.又平面α与平面ABC不重合,∴平面α与平面ABC平行.故选A.
18.如图,在长方体ABCD-A1B1C1D1中,AB=4,BC=2,CC1=3,E,F分别是BC,CD的中点,以D为原点,分别以DA,DC,DD1所在直线为坐标轴建立空间直角坐标系,则平面D1EF的一个法向量是　　　　　. 
解析 ∵在长方体ABCD-A1B1C1D1中,AB=4,BC=2,CC1=3,E,F分别是BC,CD的中点,以D为原点,分别以DA,DC,DD1所在直线为坐标轴建立空间直角坐
是(-6,3,2).
19.在△ABC中,A(1,-2,-1),B(0,-3,1),C(2,-2,1).若向量n与平面ABC垂直,且|n|= ,则n的坐标为　　 　　. 
(-2,4,1)或(2,-4,-1)
解得y=4或y=-4.当y=4时,x=-2,z=1;当y=-4时,x=2,z=-1.∴n的坐标为(-2,4,1)或(2,-4,-1).
20. 如图所示,平面CDEF⊥平面ABCD,且四边形ABCD为平行四边形, ∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,
(1)证明 ∵平面CDEF⊥平面ABCD,ED⊥CD,ED⊂平面CDEF,平面CDEF∩平面ABCD=CD,∴ED⊥平面ABCD,AD⊂平面ABCD,即ED⊥AD.过F作FG⊥DC于G,过G作GH∥AD交AB于H.∵四边形CDEF为直角梯形,AB=3EF=3,∴ED∥FG,即FG⊥AD,则FG⊥HG,且HG= ,HB=2,∠GHB=45°,∴BG2=HG2+HB2-2HG×HBcs∠GHB,得BG2=2,即HG2+BG2=HB2,∴HG⊥BG,而BG∩FG=G,即HG⊥平面FBG,又BF⊂平面FBG,∴HG⊥BF,故AD⊥BF.
(2)解 以D为原点,平面ABCD上过点D垂直于DC的直线为x轴,DC所在直线为y轴,DE所在直线为z轴,建立空间直角坐标系,如图所示,
设平面BDM的法向量为n=(x1,y1,z1),