



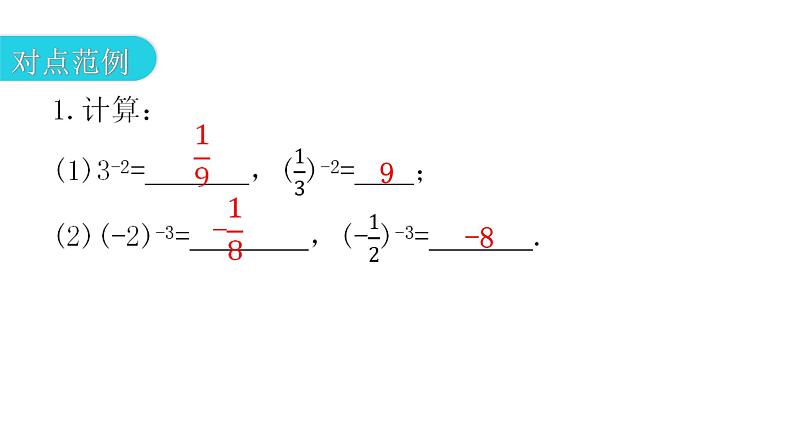
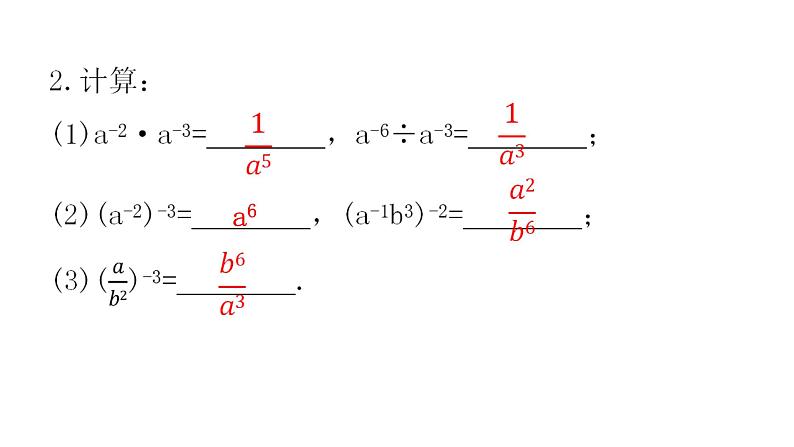


所属成套资源:全套人教版八年级数学上册课时教学课件
初中数学人教版八年级上册第十五章 分式15.2 分式的运算15.2.3 整数指数幂教学课件ppt
展开
这是一份初中数学人教版八年级上册第十五章 分式15.2 分式的运算15.2.3 整数指数幂教学课件ppt,共24页。PPT课件主要包含了知识重点,对点范例,典型例题,举一反三,am+n,amn,anbn,×10-4,06×10-2,-78×10-5等内容,欢迎下载使用。
(2)将负整数指数幂的性质融入正整数指数幂的运算中,可得到整数指数幂的运算性质,可归结为①am·an=_______;②(am )n=______;③(ab)n=________.其中m,n均为整数.
把一个数A记成a×10n的形式(其中a的取值范围是1≤|a|<10,n是整数).如:±0.000 01=±1×10-5.
3.用科学记数法表示下列各数:(1)0.000 50=____________;(2)0.060 6=________________;(3)-0.000 078=________________.
思路点拨:根据有理数的负整数指数幂的性质进行计算,注意运算结果中幂的符号与指数的正负无关,只与指数的奇偶和底数的符号有关.
思路点拨:根据乘方运算、负整数指数幂的意义以及零指数幂的意义即可求出答案.
解:原式=-4+4×1-9=-9.
【例3】计算:(1)a-2b2·(a2b-2)-3;
思路点拨:根据整数指数幂的运算性质化简求解即可.注意结果要将负整数指数幂化为正整数指数幂的形式.
6.计算:(1)(a3b-1)-2·(a-3b2)2;
(2)(xy-2)-3÷x0·y3÷x-1y5.
【例4】芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.000 002 01 kg,将0.000 002 01用科学记数法表示为( )×10-5×10-6×10-5D.20.1×10-4
思路点拨:小于1的正数利用科学记数法表示为a×10-n的形式.
7.信息技术发展的今天,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到28 nm,已知1 nm=10-9 m,则28 nm用科学记数法表示是( )A.2.8×10-8 mB.2.8×10-9 mC.28×10-9 mD.2.8×10-10 m
【例5】计算(结果用科学记数法表示):(1)(-3.5×10-13)×(-4×10-7);
思路点拨:先把系数相乘除,再按幂的乘除法则计算即可.
解:原式=(-3.5)×(-4)×10-13×10-7=14×10-20=1.4×10-19.
(2)(5.2×10-9)÷(-4×10-3).
解:原式=[5.2÷(-4)]×(10-9÷10-3)=-1.3×10-6.
8.计算(结果用科学记数法表示):(1)(2×10-3)2×(3×10-3);
解:原式=4×10-6×3×10-3=12×10-9=1.2×10-8.
(2)(2×10-4)÷(-2×10-7)-3.
思路点拨:利用题中的新定义计算得到结果.
相关课件
这是一份初中数学15.2.3 整数指数幂授课课件ppt,共27页。PPT课件主要包含了学习目标,新课导入,复习引入,负整数指数幂,不为0,am+n,am-n,anbn,amn,整数指数幂的运算性质等内容,欢迎下载使用。
这是一份人教版八年级上册第十五章 分式15.2 分式的运算15.2.3 整数指数幂优质课件ppt,共15页。PPT课件主要包含了学习目标,自主预学,a5÷a3a2,合作互学,我们现在已经知道了,a2+–3,解原式a–1,展示竞学,精讲导学,小结评学等内容,欢迎下载使用。
这是一份人教版八年级上册第十五章 分式15.2 分式的运算15.2.3 整数指数幂背景图课件ppt,共18页。PPT课件主要包含了此时此刻之前,探究新知,深入探究,成果归纳,应用初试,课堂检测1,互为倒数,课堂检测2,拓展探究,同底数幂的除法等内容,欢迎下载使用。









