浙江省A9协作体2023-2024学年高二数学上学期暑假返校联考试题（Word版附答案）

这是一份浙江省A9协作体2023-2024学年高二数学上学期暑假返校联考试题（Word版附答案），共8页。试卷主要包含了考试结束后，只需上交答题卷，在复平面内，复数，则等内容，欢迎下载使用。
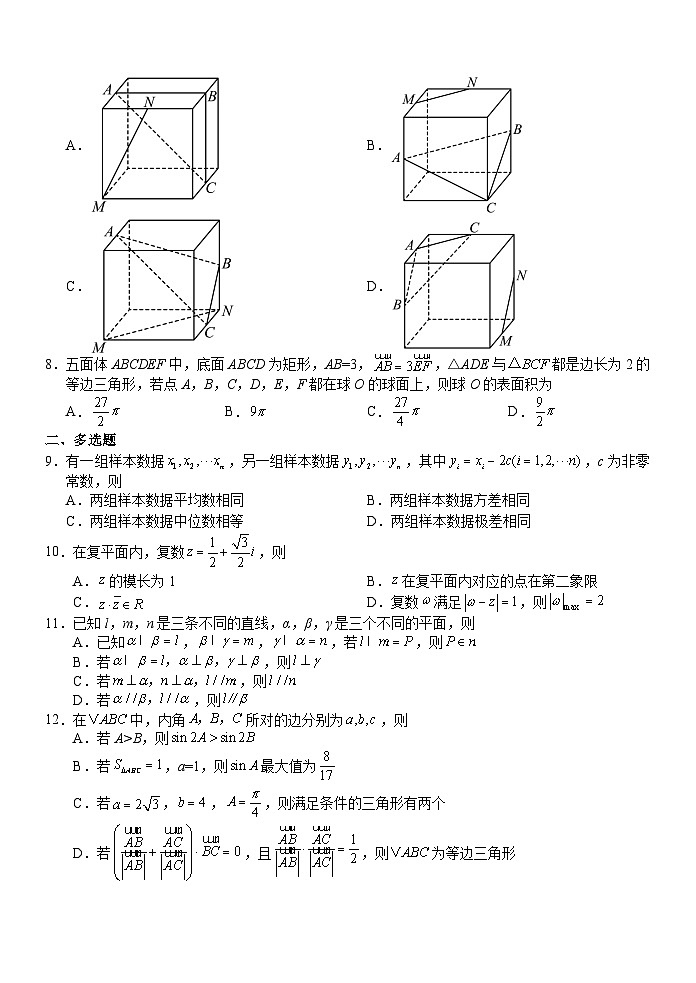
绝密★考试结束前 浙江省A9协作体暑假返校联考高二数学试题卷 考生须知：1．本卷满分150分，考试时间120分钟；2．答题前务必将自己的姓名，准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的地方。3．答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范答题，在本试卷纸上答题一律无效。4．考试结束后，只需上交答题卷。第Ⅰ卷一、单选题1．若，则复数的虚部为A．i B．1 C．-1 D．-i 2．如图所示，等腰梯形是平面图形ABCD用斜二测画法得到的直观图，，则平面图形ABCD的面积为A．  B．12C．  D．63．抛掷两枚质地均匀的骰子，记事件A=“第一枚骰子奇数面朝上”，事件B=“第二枚骰子偶数面朝上”，事件C=“两枚骰子向上点数之和为7”.则下列结论正确的是A．A与B对立 B．A与C互斥 C． D．B与C独立4．已知向量，，若是在上的投影向量，则A． B． C． D． 5．在中，内角A，B，C所对的边分别为，，，将该三角形绕AC边旋转360°得一个旋转体，则该旋转体体积为A． B． C． D． 6．一组数据由6个数组成，将其中一个数由4改为6，另一个数由12改为10，其余数不变，得到新的一组数据，则新的一组数的方差减去原一组数的方差的差为A．4 B．3 C．-4 D．-37．如图，点，，，，为正方体的顶点或所在棱的中点，则下列各图中，不满足直线平面的是A．  B．C． D．8．五面体ABCDEF中，底面ABCD为矩形，AB=3，，△ADE与都是边长为2的等边三角形，若点A，B，C，D，E，F都在球O的球面上，则球O的表面积为A． B． C． D． 二、多选题9．有一组样本数据，另一组样本数据，其中，c为非零常数，则A．两组样本数据平均数相同 B．两组样本数据方差相同C．两组样本数据中位数相等 D．两组样本数据极差相同10．在复平面内，复数，则A．的模长为1   B．在复平面内对应的点在第二象限C．   D．复数满足，则 11．已知l，m，n是三条不同的直线，α，β，γ是三个不同的平面，则A．已知，，，若，则 B．若，则C．若，则D．若，则12．在中，内角所对的边分别为，则A．若A>B，则 B．若，a=1，则最大值为 C．若，，，则满足条件的三角形有两个D．若，且，则为等边三角形第Ⅱ卷三、填空题13．复数是关于的方程的一个根，则   ▲   ．14．某人在湖面之上2米处测得空中一气球的仰角为30°，且测得湖中气球倒影的俯角为60°，若不考虑水的折射和球的体积，则气球离水面的高度为   ▲   米．15．在中，，，，则的长为   ▲   ．16．已知三棱锥ABCD中，AB⊥CD，且CD与平面ABD所成角余弦值为，当取得最大值时，二面角C-AB-D的正弦值为   ▲   ．四、解答题17．已知向量与的夹角为，且，是单位向量．（1）分别求和的值；（2）若与共线，求．   18．杭州2022年第19届亚运会将于2023年9月23日至10月8日举行．随着亚运会的临近，亚运会的热度持续提升．为让更多的人了解亚运会运动项目和亚运精神，某中学举办了亚运会知识竞赛，并从中随机抽取了100名学生的成绩，绘制成如图所示的频率分布直方图．（1）试根据频率分布直方图求出这100名学生中成绩低于60分的人数；（2）试估计这100名学生成绩的第75百分位数；（3）若采用分层抽样的方法从成绩在，，的学生中共抽取6人参加志愿者活动．现从这6人中随机抽取2人分享活动经验，求抽取的2人成绩都在的概率．     19．在中，内角A，B，C所对的边分别为a，b，c，且．（1）求角A；（2）若，，的角平分线交BC于D，求AD的长．    20．如图，在四棱锥中，底面是边长为的正方形，侧面为等腰直角三角形，且，点为棱上的点，平面与棱交于点．（1）求证：；（2）若，，求证平面平面．       21．如图，在中，，，，点D，E分别在，上且满足，，点在线段上．（1）若，求；（2）若，且求；（3）求的最小值．       22．如图1，在矩形中，已知，E为的中点.将沿向上翻折，进而得到多面体（如图2）.（1）当平面⊥平面，求直线与平面所成角的正切值；（2）在翻折过程中，求二面角的最大值.   浙江省A9协作体暑假返校联考高二数学参考答案12345678BADCBCDA 9101112BDACDACBCD13．3         14．4           15．               16．17．（1），； （2） （1），.（2）若与共线，则存在，使得，即，又因为向量与不共线，所以，解得，所以.18．（1）18人；（2）82.5；（3）。（1）由频率分布直方图中数据可知： （2）成绩小于80的频率为，成绩在的频率为，因为，所以这名学生成绩的第百分位数在内，所以随机抽取的100名学生成绩的第75百分位数为.（3）因为成绩在，，的学生人数所占比例为3:2:1，所以从成绩在，，所抽取人数分别应抽取3人，2人，1人.记抽取成绩在的3人为，成绩在为.，，共15种，抽取的2人成绩都在的是，共3种，抽取的人成绩都在的概率为.19．（1）；（2）2。（1），由正弦定理可得：，而，故，因为，所以，又，所以，（2）由余弦定理可得，，因为，解得：，由可得，，解得：．20．（1）见详解（2）见详解（1）证明：因为底面是正方形，所以，平面，平面，所以平面，又因为平面与交于点，平面，平面平面， 所以．（2）证明：侧面为等腰直角三角形，且，即，，因为，，且两直线在平面内，可得平面，因为平面，则．又因为，，且两直线在平面内，则平面，因为平面，则，因为，所以为等腰三角形，所以点为的中点.又因为，所以为等腰直角三角形，因为，所以AP⊥面，因为面APD，所以面APD⊥面.21．（1）；（2）；（3）。（1）点在线段上，则，使得，t>0，则，又，，故，根据题干可知：，，于是，（2），由，，且，故，又由，，，代入数据可得t=1 ，故. （3）取中点，则，由，于是，由，，故为等边三角形，故，根据中位线可知，//，于是，在中根据余弦定理可得，为锐角，又，故过作的高线时，垂足点落在线段上，由题意垂足点为时，最小.最小值为，，在中，根据余弦定理可求得，即，故的最小值为.22．（1）；（2） （1）解三角形得到AC⊥DE，，。因为面⊥面BCD，面面BCD=DE，所以面BCD。    所以是直线与平面所成角。所以.（2）如图2，过作，垂足为H，过H作，垂足为G，连接.因为平面平面，所以.又因为平面，所以平面.因为平面，所以.又因为平面，所以平面.因为平面，所以.所以是二面角的平面角.在翻折过程中，设.在矩形中，由，E为的中点，得.在直角三角形中，，所以，因为，所以，所以，所以.在直角三角形中，.设，所以.所以，即.解得，当时，等号成立，故，因为，所以，