


重庆市巴南区2022-2023学年七下数学期末质量跟踪监视试题含答案
展开
这是一份重庆市巴南区2022-2023学年七下数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
重庆市巴南区2022-2023学年七下数学期末质量跟踪监视试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.下列说法正确的是( )A.顺次连接任意一个四边形四边的中点,所得到的四边形一定是平行四边形B.平行四边形既是中心对称图形,又是轴对称图形C.对角线相等的四边形是矩形D.只要是证明两个直角三角形全等,都可以用“HL”定理2.如图,已知在平行四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两点,则以下条件不能判断四边形
上的两点,则以下条件不能判断四边形![]() 是平行四边形的是( )
是平行四边形的是( )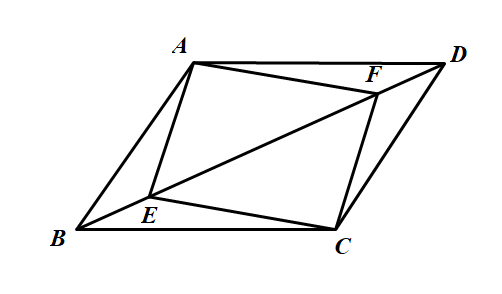 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡,它们的使用寿命如表所示:使用寿命x/h60≤x<100100≤x<140140≤x<180灯泡只数303040这批灯泡的平均使用寿命是( )A.112 h B.124 h C.136 h D.148 h4.如图,在
3.某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡,它们的使用寿命如表所示:使用寿命x/h60≤x<100100≤x<140140≤x<180灯泡只数303040这批灯泡的平均使用寿命是( )A.112 h B.124 h C.136 h D.148 h4.如图,在![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 交
交![]() 与点
与点![]() ,则
,则![]() 与
与![]() 的比值是( )
的比值是( )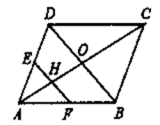 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,在已知的△ABC中,按以下步骤作图:①分别以A,B为圆心,以大于
5.如图,在已知的△ABC中,按以下步骤作图:①分别以A,B为圆心,以大于![]() AB的长为半径作弧,两弧相交于两点EF;②作直线EF交BC于点D连接AD.若AD=AC,∠C=40°,则∠BAC的度数是( )
AB的长为半径作弧,两弧相交于两点EF;②作直线EF交BC于点D连接AD.若AD=AC,∠C=40°,则∠BAC的度数是( )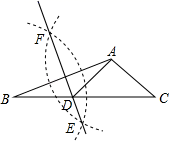 A.105° B.110° C.I15° D.120°6.如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )
A.105° B.110° C.I15° D.120°6.如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )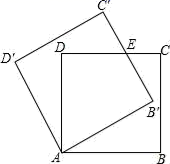 A.
A.![]() B.
B.![]() C.1 D.
C.1 D.![]() ﹣17.在平面直角坐标系中,点
﹣17.在平面直角坐标系中,点![]() 在第一象限,若点
在第一象限,若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,则
上,则![]() 的值为( )A.3 B.2 C.1 D.-18.如图,
的值为( )A.3 B.2 C.1 D.-18.如图,![]() 分别是矩形
分别是矩形![]() 的边
的边![]() 上的点,将四边形
上的点,将四边形![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 处,已知
处,已知![]() ,则
,则![]() 的长是( )
的长是( )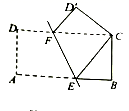 A.4 B.5 C.6 D.79.如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,
A.4 B.5 C.6 D.79.如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,![]() ,则四边形EFCD的周长为
,则四边形EFCD的周长为![]()
![]()
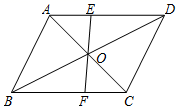 A.14 B.13 C.12 D.1010.如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
A.14 B.13 C.12 D.1010.如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )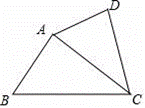 A.∠DAC=∠ABC B.AC是∠BCD的平分线 C.AC2=BC•CD D.
A.∠DAC=∠ABC B.AC是∠BCD的平分线 C.AC2=BC•CD D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.分式
二、填空题(本大题共有6小题,每小题3分,共18分)11.分式![]() 与
与![]() 的最简公分母是__________.12.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PE⊥AC于F,则EF的最小值_____.
的最简公分母是__________.12.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PE⊥AC于F,则EF的最小值_____.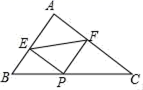 13.在平面直角坐标系xOy中,点A(2,﹣3)关于x轴对称的点B的坐标是______.14.关于
13.在平面直角坐标系xOy中,点A(2,﹣3)关于x轴对称的点B的坐标是______.14.关于![]() 的一元二次方程
的一元二次方程![]() 有一个解是
有一个解是![]() ,则
,则![]() __________.15.如图,在▱ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:①DE=4
__________.15.如图,在▱ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:①DE=4![]() ;②S△AED=
;②S△AED=![]() S四边形ABCD;③DE平分∠ADC;④∠AED=∠ADC.其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)
S四边形ABCD;③DE平分∠ADC;④∠AED=∠ADC.其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)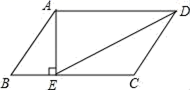 16.一辆汽车,新车购买价20万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二,三年的年折旧率相同.已知在第三年年末,这辆车折旧后价值11.56万元,如果设这辆车第二、三年的年折旧率为x,那么根据题意,列出的方程为_____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,
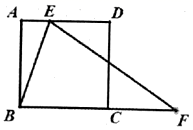
16.一辆汽车,新车购买价20万元,第一年使用后折旧20%,以后该车的年折旧率有所变化,但它在第二,三年的年折旧率相同.已知在第三年年末,这辆车折旧后价值11.56万元,如果设这辆车第二、三年的年折旧率为x,那么根据题意,列出的方程为_____.三、解下列各题(本大题共8小题,共72分)17.(8分)如图,![]() 是正方形
是正方形![]() 的边
的边![]() 上的动点,
上的动点,![]() 是边
是边![]() 延长线上的一点,且
延长线上的一点,且![]() ,
,![]() ,设
,设![]() ,
,![]() .
. (1)当
(1)当![]() 是等边三角形时,求
是等边三角形时,求![]() 的长;(2)求
的长;(2)求![]() 与
与![]() 的函数解析式,并写出它的定义域;(3)把
的函数解析式,并写出它的定义域;(3)把![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,试探索:
处,试探索:![]() 能否为等腰三角形?如果能,请求出
能否为等腰三角形?如果能,请求出![]() 的长;如果不能,请说明理由.
的长;如果不能,请说明理由.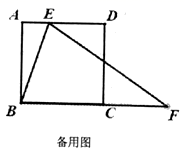 18.(8分)已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式. 19.(8分)本工作,某校对八年级一班的学生所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图所示的两幅不完整的统计图(校服型号以身高作为标准,共分为6种型号)。条形统计图
18.(8分)已知一次函数的图象过点(3,5)与点(﹣4,﹣9),求这个一次函数的解析式. 19.(8分)本工作,某校对八年级一班的学生所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图所示的两幅不完整的统计图(校服型号以身高作为标准,共分为6种型号)。条形统计图 扇形统计图
扇形统计图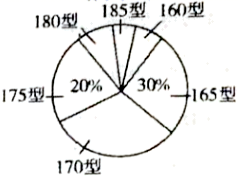 根据以上信息,解答下列问题:(1)该班共有多少名学生?其中穿
根据以上信息,解答下列问题:(1)该班共有多少名学生?其中穿![]() 型校服的学生有多少名?(2)在条形统计图中,请把空缺部分补充完整;(3)在扇形统计图中,请计算
型校服的学生有多少名?(2)在条形统计图中,请把空缺部分补充完整;(3)在扇形统计图中,请计算![]() 型校服所对应的扇形圆心角的大小;(4)求该班学生所穿校服型号的中位数。 20.(8分)在“2019慈善一日捐”活动中,某校八年级(1)班40名同学的捐款情况如下表:捐款金额(元)203050a80100人数(人)2816x47根据表中提供的信息回答下列问题:(1)x的值为________ ,捐款金额的众数为________元,中位数为________元.(2)已知全班平均每人捐款57元,求a的值. 21.(8分)如图,直线经过矩形
型校服所对应的扇形圆心角的大小;(4)求该班学生所穿校服型号的中位数。 20.(8分)在“2019慈善一日捐”活动中,某校八年级(1)班40名同学的捐款情况如下表:捐款金额(元)203050a80100人数(人)2816x47根据表中提供的信息回答下列问题:(1)x的值为________ ,捐款金额的众数为________元,中位数为________元.(2)已知全班平均每人捐款57元,求a的值. 21.(8分)如图,直线经过矩形![]() 的对角线
的对角线![]() 的中点
的中点![]() ,分别与矩形的两边相交于点
,分别与矩形的两边相交于点![]() 、
、![]() .
.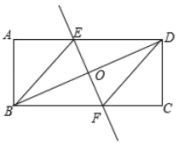 (1)求证:
(1)求证:![]() ;(2)若
;(2)若![]() ,则四边形
,则四边形![]() 是______形,并说明理由;(3)在(2)的条件下,若
是______形,并说明理由;(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的面积. 22.(10分)我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.(发现与证明)▱ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.结论1:△AB′C与▱ABCD重叠部分的图形是等腰三角形;结论2:B′D∥AC…(应用与探究)在▱ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB′C,连结B′D.若以A、C、D、B′为顶点的四边形是正方形,求AC的长.(要求画出图形)
的面积. 22.(10分)我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.(发现与证明)▱ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.结论1:△AB′C与▱ABCD重叠部分的图形是等腰三角形;结论2:B′D∥AC…(应用与探究)在▱ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB′C,连结B′D.若以A、C、D、B′为顶点的四边形是正方形,求AC的长.(要求画出图形)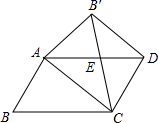 23.(10分)作图:如图,平面内有 A,B,C,D 四点 按下列语句画图:
23.(10分)作图:如图,平面内有 A,B,C,D 四点 按下列语句画图: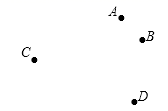 (1)画射线 AB,直线 BC,线段 AC(2)连接 AD 与 BC 相交于点 E. 24.(12分)解不等式组:
(1)画射线 AB,直线 BC,线段 AC(2)连接 AD 与 BC 相交于点 E. 24.(12分)解不等式组:![]() ,并把解集在数轴上表示出来. 参考答案 一、选择题(每小题3分,共30分)1、A2、A3、B4、C5、D6、D7、C8、B9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、
,并把解集在数轴上表示出来. 参考答案 一、选择题(每小题3分,共30分)1、A2、A3、B4、C5、D6、D7、C8、B9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、2.413、(2,3)14、-315、①②③16、20(1﹣20%)(1﹣x)2=11.1. 三、解下列各题(本大题共8小题,共72分)17、(1)
12、2.413、(2,3)14、-315、①②③16、20(1﹣20%)(1﹣x)2=11.1. 三、解下列各题(本大题共8小题,共72分)17、(1)![]() ;(1)
;(1)![]() ;(3)答案见解析.18、y=2x﹣1.19、(1)50,10;(2)见解析;(3)14.4°;(4)170型20、(1)3;50;50 (2)121、 (1)证明见解析;(2)菱,理由见解析;(3)
;(3)答案见解析.18、y=2x﹣1.19、(1)50,10;(2)见解析;(3)14.4°;(4)170型20、(1)3;50;50 (2)121、 (1)证明见解析;(2)菱,理由见解析;(3)![]() .22、 [发现与证明]:证明见解析;[应用与探究]:AC的长为
.22、 [发现与证明]:证明见解析;[应用与探究]:AC的长为![]() 或1.23、答案见解析24、
或1.23、答案见解析24、![]()
相关试卷
这是一份重庆市江北区2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份山东泰安2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了一元二次方程的根是,整数满足,则的值为等内容,欢迎下载使用。
这是一份2022-2023学年黄冈中学数学七下期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列各式中,最简二次根式为等内容,欢迎下载使用。








