数学必修 第一册2.1 等式性质与不等式性质优质课教学设计及反思

2.1 等式性质与不等式性质单元设计

第2课时  等式性质与不等式性质

一.教学内容  

1.类比等式性质得不等式的基本性质，等式与不等式的共性与差异.

2.不等式基本性质的证明与应用

二．教学目标

1.通过了解等式的性质;掌握不等式的基本性质，并能运用这些性质解决有关问题．

2.通过对不等式性质的证明，体会类比思想在数学中的应用，提升逻辑思维能力和数学思维的严密性.

三．教学重难点

1. 重点：不等式的基本性质

2.难点：不等式性质的证明与综合应用

四．教学过程设计

问题1；如何求方程5x+4=0的解？解方程的理论依据是什么？

 学生演练：先将等式两边同时减4，得

再将等式两边同时除以5，得,

所以方程的解是. 

师：解方程的理论依据是等式的性质。

等式性质

性质1   如果那么（对称性）

性质2   如果那么（传递性）

性质3   如果那么

性质4   如果那么

性质5   如果那么

性质3,4,5是等式对四则运算的不变性.

【设计意图】通过解方程例子，自然而然引出等式的性质。让学生思维有个过渡，为后面的类比思想作铺垫。

问题2  类比等式 的基本性质，你能猜想不等式的基本性质吗？并进行证明吗？

师生活动：

师;类比等式的性质1，2，可以猜想不等式有如下性质：

（1）如果甲同学比乙同学大，那么乙同学比甲同学小，对吗？

（2）如果甲同学比乙同学大，且乙同学比丙同学大，那甲同学比丙同学大，对吗？          （3）如果，那么a＋c与b＋c的大小关系如何？ac与bc呢？

（4）不等式还有哪些性质？

生： (1), (2)对；

（3）如果.

当时，；当时，；当时，.

不等式性质

性质1  如果如果，那么.

性质2  如果，那么(传递性）

符号表示：

性质3  如果，那么

文字表示：不等式的两边都加上同一个实数，所得不等式与原不等式同向.

移项法则：

性质4   如果那么； 如果那么

文字表示：不等式的两边同乘一个正数，所得不等式与原不等式同向；不等式的两边同乘一个负数，所得不等式与原不等式反向.

性质5  如果，那么

注意：同向不等式相加得同向不等式，并无相减。

性质6  如果，那么

注意：同向不等式相乘得同向不等式，并无相除。另外“大于0”的条件不能忽略。      性质7  如果那么.

注意：“大于0”的条件不能忽略。

重要结论：如果,那么,如果那么0.

  【设计意图】通过问题作出类比，从等式性质得不等式的基本性质，让学生了解等式与不等式的共性与差异. 从而培养学生解决问题的能力，提升逻辑推理能力。

五.例题分析

例1.给出下列命题：

①若ab>0，a>b，则<；

②若a>b，c>d，则a－c>b－d；

③对于正数a，b，m，若a<b，则<.其中真命题的序号是________．

学生分析：例1.答案　①③

解析：对于①，若ab>0，则>0，又a>b，所以>，所以<，所以①正确；

对于②，若a＝7，b＝6，c＝0，d＝－10，则7－0<6－(－10)，②错误；

对于③，对于正数a，b，m，若a<b，则am<bm，所以am＋ab<bm＋ab，

所以0<a(b＋m)<b(a＋m)，又>0，所以<，③正确．

综上，真命题的序号是①③.

问题3：请说明每一步用到的是不等式的哪一条性质？

  学生回答，归纳总结。

师：方法总结:首先要注意不等式成立的条件，在解决选择题时，可利用特值法进行排除，注意取值时一是满足题设条件，二是取值简单，便于计算．

例2：如果a，b，c满足，且，那么下列不等式中不一定成立的是(　　)

学生解析： [答案]  C

由于且，因此，b的符号不确定，则不一定成立的不等式可能与b有关．不难发现，当C中的b为0时，不等式不成立．

师：方法总结：利用不等式判断正误的2种方法

(1)直接法：对于说法正确的，要利用不等式的相关性质证明；对于说法错误的只需举出一个反例即可．

(2)特殊值法：注意取值一定要遵循三个原则：一是满足题设条件；二是取值要简单，便于验证计算；三是所取的值要有代表性．

 【设计意图】通过例题，运用不等式解决问题，加深对不等式的性质的理解。同时总结不等式比较大小的方法。培养逻辑推理能力。

六.巩固练习

1. 完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20000元,设木工x人,瓦工y人,则工人满足的关系式是(　　)

A.5x+4y<200   B.5x+4y≥200

C.5x+4y=200   D.5x+4y≤200

2.下列命题中正确的是(　　)

A．若a>b，c>d，则ac>bd           B．若ac>bc，则a>b

C．若<，则a<b                 D．若a>b，c>d，则a－c>b－d

3.(多选题)若,则下列命题:

(1)     .  (2). (3).  (4)

中能成立的是(　　)

A.(1)       B.(2)      C.(3)      D.(4)

4.已知－1≤a＋b≤1,1≤a－2b≤3，求a＋3b的取值范围．

【设计意图】通过不等式的判断、证明，使学生熟练掌握不等式的性质，培养学生解决问题的能力。

    七．课堂小结，反思感悟

       1.知识总结：

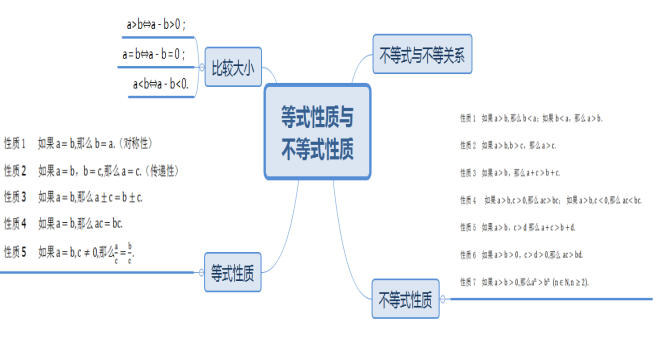
2.学生反思：

（1）通过这节课，你学到了什么知识？

（2）在解决问题时，用到了哪些数学思想？

  【设计意图】通过总结，让学生进一步巩固不等式的性质，辨析不等式成立的条件,树立用不等式解决相关问题的意识。