


高中数学人教A版 (2019)必修 第一册4.3 对数精品达标测试
展开![]() 4.3对数同步训练
4.3对数同步训练
一、选择题(共10题,第10题为多选)
- 计算:


A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 计算:


A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 若
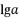 ,
,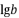 是方程
是方程 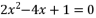 的两个根,则
的两个根,则  的值等于
的值等于 
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
- 已知
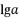 ,
,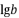 是方程
是方程 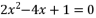 的两个根,则
的两个根,则  的值是
的值是 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 设
 ,
, ,
,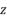 为正数,且
为正数,且 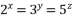 ,则
,则 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 若
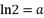 ,
,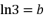 ,则
,则 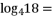

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 计算
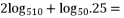

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 已知
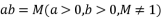 ,
,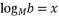 ,则
,则 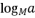 的值为
的值为 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- 地震里氏震级是地震强度大小的一种度量.地震释放的能量
 (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级  之间的关系为
之间的关系为 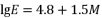 .已知两次地震里氏震级分别为
.已知两次地震里氏震级分别为 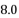 级和
级和  级,若它们释放的能量分别为
级,若它们释放的能量分别为 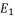 和
和 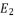 ,则
,则  的值所在的区间为
的值所在的区间为 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
- (多选)设
 ,
,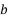 ,
, 都是正数,且
都是正数,且 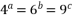 ,那么
,那么 
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(共5题)
- 若
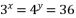 ,则
,则 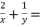 .
. - 已知
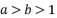 .若
.若 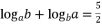 ,
,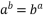 ,则
,则  ,
, .
. - 已知函数
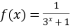 ,则
,则 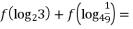 .
. - 若
 ,
,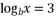 ,
,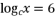 ,则
,则 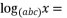 .
. -
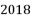 年
年  月,阿贝尔奖和菲尔兹奖双料得主,英国
月,阿贝尔奖和菲尔兹奖双料得主,英国 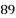 岁高龄的著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在
岁高龄的著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动.在  年,德国数学家黎曼向科学院提交了题目为《论小于给定数值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前著名的数学家欧拉也曾研究过这个问题,并得到小于数字
年,德国数学家黎曼向科学院提交了题目为《论小于给定数值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前著名的数学家欧拉也曾研究过这个问题,并得到小于数字  的素数个数大约可以表示为
的素数个数大约可以表示为  的结论.若根据欧拉得出的结论,估计
的结论.若根据欧拉得出的结论,估计 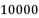 以内的素数个数为 (素数即质数,
以内的素数个数为 (素数即质数,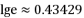 ,计算结果取整数)
,计算结果取整数)
三、解答题(共5题)
- 解答下列问题.
(1) 计算:![]() ;(2) 设
;(2) 设 ![]() ,求
,求 ![]() 的值.
的值.
- 请回答下列问题:
(1) 已知 ![]() ,
,![]() ,用
,用 ![]() ,
,![]() 表示
表示 ![]() ;
;
(2) 解方程:![]() .
.
- 若
 ,
,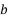 是方程
是方程 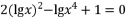 的两个实数根,求
的两个实数根,求 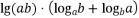 的值.
的值.
- 已知函数
 .
.
(1) 判断 ![]() 的奇偶性;(2) 若
的奇偶性;(2) 若 ![]() ,
,![]() ,求
,求 ![]() ,
,![]() 的值.
的值.
- 计算:
(1) ![]() .(2)
.(2) ![]() .
.
答案
一、选择题(共10题)
1. 【答案】D
【解析】 ![]() .
.
2. 【答案】D
【解析】 ![]() .
.
3. 【答案】A
【解析】由根与系数的关系,
得 ![]() ,
,![]() ,
,
所以
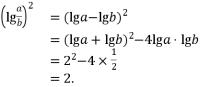
4. 【答案】B
【解析】因为 ![]() ,
,![]() 是方程
是方程 ![]() 的两个根,,
的两个根,,
所以结合根与系数的关系得 ![]() ,
,![]() ,
,
所以
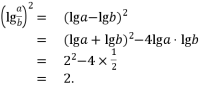
5. 【答案】D
【解析】解法一(特值法):
令 ![]() ,则由已知条件可得
,则由已知条件可得 ![]() ,
,![]() ,
,
所以 ![]() ,
,![]() ,
,
从而 ![]() ,
,![]() ,
,
则 ![]() .
.
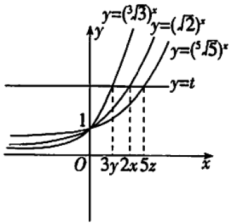
解法二(数形结合法):
由 ![]() ,可设
,可设 ![]() ,
,
因为 ![]() ,
,![]() ,
,![]() 为正数,
为正数,
所以 ![]() ,
,
因为 ![]() ,
,![]() ,
,
所以 ![]() ;
;
因为 ![]() ,
,![]() ,
,
所以 ![]() ,
,
所以 ![]() .
.
分别作出 ![]() ,
,![]() ,
,![]() 的图象及直线
的图象及直线 ![]() ,如图,
,如图,
则 ![]() .
.
解法三(作商法):
由 ![]() ,同时取自然对数,得
,同时取自然对数,得 ![]() .
.
由 ![]() ,可得
,可得 ![]() ;
;
由 ![]() ,可得
,可得 ![]() ,
,
所以 ![]() .
.
6. 【答案】D
【解析】 ![]() .
.
7. 【答案】C
【解析】 ![]() .
.
故选C.
8. 【答案】C
【解析】因为 ![]() ,
,
所以 ![]() ,
,
所以 ![]() .
.
9. 【答案】B
10. 【答案】A;D
【解析】由题意,设 ![]() ,则
,则 ![]() ,
,![]() ,
,![]() ,
,
对于选项A,由 ![]() ,可得
,可得 ![]() ,因为
,因为 ![]() ,故A正确,B错误;
,故A正确,B错误;
对于选项C,![]() ,
,![]() ,故
,故 ![]() ,故C错误;
,故C错误;
对于选项D,![]() ,
,![]() ,故
,故 ![]() ,即D正确.
,即D正确.
二、填空题(共5题)
11. 【答案】 ![]()
【解析】解法一:![]() ,取以
,取以 ![]() 为底的对数,得
为底的对数,得 ![]() ,
,
所以 ![]() ,
,![]() ,即
,即 ![]() ,
,
故 ![]() .
.
解法二:因为 ![]() ,
,
所以 ![]() ,
,![]() ,
,
所以 ![]() .
.
12. 【答案】 ![]() ;
; ![]()
【解析】令 ![]() ,因为
,因为 ![]() ,所以
,所以 ![]() ,
,
由 ![]() 得
得 ![]() ,
,
解得 ![]() 或
或 ![]() (舍去),即
(舍去),即 ![]() ,所以
,所以 ![]() ,
,
又因为 ![]() ,所以
,所以 ![]() ,即
,即 ![]() ,即
,即 ![]() ,
,
解得 ![]() ,所以
,所以 ![]() .
.
13. 【答案】 ![]()
14. 【答案】 ![]()
【解析】因为 ![]() ,所以
,所以 ![]() ,
,
同理 ![]() ,
,![]() .
.
所以 ![]() .
.
15. 【答案】 ![]()
【解析】由题可知小于数字 ![]() 的素数个数大约可以表示为
的素数个数大约可以表示为 ![]() ,则
,则 ![]() 以内的素数的个数为
以内的素数的个数为

三、解答题(共5题)
16. 【答案】
(1) 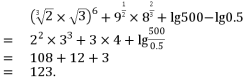
(2) 依题意得 ![]() ,
,![]() ,
,
所以 ![]() .
.
17. 【答案】
(1) 因为 ![]() ,
,
所以 ![]() ,
,
所以
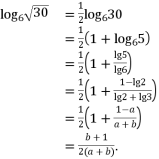
(2) ![]() ,
,
移项并整理得
![]() ,
,
所以 ![]() ,
,
解得 ![]() 或
或 ![]() ,经检验
,经检验 ![]() 为所求.
为所求.
18. 【答案】原方程可变形为 ![]() ,
,
因为 ![]() ,
,![]() 是方程
是方程 ![]() 的两个实数根,
的两个实数根,
所以 ![]() ,
,![]() ,
,
所以

19. 【答案】
(1) ![]() 的定义域为
的定义域为 ![]() ,
,![]() ,
,
故 ![]() 是奇函数.
是奇函数.
(2) 由 ![]() ,得
,得 ![]() .
.
又 ![]() ,即
,即 ![]() .
.
由 ![]() 解得
解得 ![]()
20. 【答案】
(1) ![]() .
.
(2) 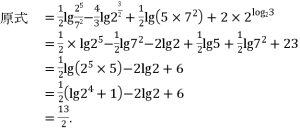
高中数学人教A版 (2019)必修 第一册4.3 对数课后练习题: 这是一份高中数学人教A版 (2019)必修 第一册4.3 对数课后练习题,共5页。
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数巩固练习: 这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数巩固练习,共12页。试卷主要包含了单选题,多选题,填空题,十七世纪之交,随着天文,解答题等内容,欢迎下载使用。
高中数学4.3 对数复习练习题: 这是一份高中数学4.3 对数复习练习题,共12页。试卷主要包含了若,则,设实数,,,满足,则的最小值是,已知数列满足,且,则 ,若,且,且,等内容,欢迎下载使用。













