

高中数学人教A版 (2019)必修 第一册4.1 指数优秀精练
展开![]() 4.2.2 指数函数的图象和性质
4.2.2 指数函数的图象和性质
一、单选题
1.函数![]() 单调递增区间为( )
单调递增区间为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 恒过定点( )
恒过定点( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.函数![]() 的单调递增区间是( )
的单调递增区间是( )
A.![]() B.[2,+∞)
B.[2,+∞)
C.![]() D.
D.![]()
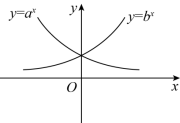
5.指数函数![]() 与
与![]() 的图象如图所示,则( )
的图象如图所示,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.函数![]() 的值域是( )
的值域是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知指数函数![]() ,且
,且![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知函数![]() ,则
,则![]() ( )
( )
A.是奇函数,且在R上是增函数
B.是偶函数,且在![]() 上是增函数
上是增函数
C.是奇函数,且在R上是减函数
D.是偶函数,且在![]() 上是减函数
上是减函数
二、多选题
9.已知函数![]() 是
是![]() 上的增函数,则实数
上的增函数,则实数![]() 的值可以是( )
的值可以是( )
A.4 B.3 C.![]() D.
D.![]()
10.函数![]() 的定义域为
的定义域为![]() ,值域
,值域![]() ,则下列结论中一定正确的有( )
,则下列结论中一定正确的有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.已知函数![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]()
B.![]() 是偶函数
是偶函数
C.![]() 的值域为
的值域为![]()
D.![]() ,且
,且![]() ,
,![]() 恒成立
恒成立
三、填空题
13.如果指数函数![]() 是
是![]() 上的减函数,则函数
上的减函数,则函数![]() 的单调递增区间为____.
的单调递增区间为____.
14.已知函数![]() 的值域为
的值域为![]() ,则
,则![]() 的取值范围为____.
的取值范围为____.
15.若![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______________.
______________.
16.函数![]() 的值域为_________.
的值域为_________.
四、解答题
17.定义在![]() 上的奇函数
上的奇函数![]() ,已知当
,已知当![]() 时,
时,![]() =
=![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
18.已知函数![]() ,且
,且![]() ,
,![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)判断函数![]() 的单调性;
的单调性;
(3)求函数![]() 的值域.
的值域.
1.C2.B3.B4.C5.C6.B7.A
9.CD.
10.BCD
11.BD
12.ACD
13.![]()
14.![]()
15.![]()
17.(1)![]()
(2)![]()
【详解】(1)因为![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,![]() 时,
时,![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,![]() ,
,
即![]() 在
在![]() 上的解析式为
上的解析式为![]() ;
;
(2)因为![]() 时,
时,![]() ,
,
所以![]() 可化为
可化为![]() ,
,
整理得![]() ,
,
令![]() ,根据指数函数单调性可得,
,根据指数函数单调性可得,
![]() 与
与![]() 都是减函数,
都是减函数,
所以![]() 也是减函数,
也是减函数,
![]() ,
,
所以![]() ,
,
故数![]() 的取值范围是
的取值范围是![]() .
.
18.(1)![]() ,
,![]()
(2)减函数
(3)![]()
【详解】(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
(2)任取![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,
设![]() ,由指数函数的单调性知,
,由指数函数的单调性知,![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() 在定义域上是减函数.
在定义域上是减函数.
(3)由第(2)问,![]() 在定义域
在定义域![]() 上是减函数,
上是减函数,
∴当![]() 时,
时,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴函数![]() 的值域为
的值域为![]() .
.
高中数学人教A版 (2019)必修 第一册4.2 指数函数测试题: 这是一份高中数学人教A版 (2019)必修 第一册4.2 指数函数测试题,共4页。
高中数学人教A版 (2019)必修 第一册4.2 指数函数一课一练: 这是一份高中数学人教A版 (2019)必修 第一册4.2 指数函数一课一练,共16页。
高中数学第四章 指数函数与对数函数4.2 指数函数课时作业: 这是一份高中数学第四章 指数函数与对数函数4.2 指数函数课时作业,共8页。试卷主要包含了设a=0,函数y=3的单调递减区间是,52,90等内容,欢迎下载使用。













