


2022-2023学年浙江省部分地区七下数学期末达标检测试题含答案
展开
这是一份2022-2023学年浙江省部分地区七下数学期末达标检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,计算的结果为,菱形与矩形都具有的性质是,下列不能判断是正方形的有等内容,欢迎下载使用。
2022-2023学年浙江省部分地区七下数学期末达标检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.若关于x的不等式组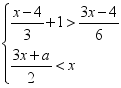 的解集为x<2,则a的取值范围是( )A.a≥﹣2 B.a>﹣2 C.a≤﹣2 D.a<﹣22.在Rt△ABC中,∠C=90°.如果BC=3,AC=5,那么AB=( )A.
的解集为x<2,则a的取值范围是( )A.a≥﹣2 B.a>﹣2 C.a≤﹣2 D.a<﹣22.在Rt△ABC中,∠C=90°.如果BC=3,AC=5,那么AB=( )A.![]() B.4 C.4或
B.4 C.4或![]() D.以上都不对3.如图,在四边形ABCD中,对角线AC与BD相交于点O,已知AB∥DC,则添加下列结论中的一个条件后,仍不能判定四边形ABCD是平行四边形的是( )
D.以上都不对3.如图,在四边形ABCD中,对角线AC与BD相交于点O,已知AB∥DC,则添加下列结论中的一个条件后,仍不能判定四边形ABCD是平行四边形的是( )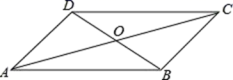 A.AO=CO B.AC=BD C.AB=CD D.AD∥BC4.计算
A.AO=CO B.AC=BD C.AB=CD D.AD∥BC4.计算![]() 的结果为( )A.
的结果为( )A.![]() B.±5 C.-5 D.55.菱形与矩形都具有的性质是( ).A.对角相等 B.四边相等 C.对角线互相垂直 D.四角相等6.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx﹣k的图象大致是( )A.
B.±5 C.-5 D.55.菱形与矩形都具有的性质是( ).A.对角相等 B.四边相等 C.对角线互相垂直 D.四角相等6.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx﹣k的图象大致是( )A.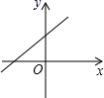 B.
B.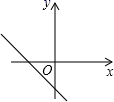 C.
C.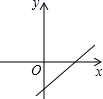 D.
D.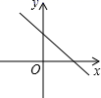 7.若n边形的内角和等于外角和的2倍,则边数n为( )A.n=4 B.n=5 C.n=6 D.n=78.下列不能判断是正方形的有( )A.对角线互相垂直的矩形 B.对角线相等的矩形C.对角线互相垂直且相等的平行四边形 D.对角线相等的菱形9.如图,四边形ABCD是菱形,AB=5,AC=6,AE⊥BC于E,则AE等于( )
7.若n边形的内角和等于外角和的2倍,则边数n为( )A.n=4 B.n=5 C.n=6 D.n=78.下列不能判断是正方形的有( )A.对角线互相垂直的矩形 B.对角线相等的矩形C.对角线互相垂直且相等的平行四边形 D.对角线相等的菱形9.如图,四边形ABCD是菱形,AB=5,AC=6,AE⊥BC于E,则AE等于( ) A.4 B.
A.4 B.![]() C.
C.![]() D.510.如图是一次函数y=x-3的图象,若点P(2,m)在该直线的上方,则m的取值范围是( )
D.510.如图是一次函数y=x-3的图象,若点P(2,m)在该直线的上方,则m的取值范围是( ) 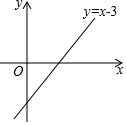 A.m>-3 B.m>0 C.m>-1 D.m<3二、填空题(本大题共有6小题,每小题3分,共18分)11.廖老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)432l0人数34111则这10名学生周末利用网络进行学习的平均时间是________小时.12.若正比例函数
A.m>-3 B.m>0 C.m>-1 D.m<3二、填空题(本大题共有6小题,每小题3分,共18分)11.廖老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:时间(单位:小时)432l0人数34111则这10名学生周末利用网络进行学习的平均时间是________小时.12.若正比例函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 的取值范围为__________.13.某市出租车白天的收费起步价为10元,即路程不超过
的取值范围为__________.13.某市出租车白天的收费起步价为10元,即路程不超过![]() 时收费10元,超过部分每千米收费2元,如果乘客白天乘坐出租车的路程为
时收费10元,超过部分每千米收费2元,如果乘客白天乘坐出租车的路程为![]() ,乘车费为
,乘车费为![]() 元,那么
元,那么![]() 与
与![]() 之间的关系式为__________________.14.为了增强青少年的防毒拒毒意识,学校举办了一次“禁毒教育”演讲比赛,其中某位选手的演讲内容、语言表达、演讲技巧这三项得分分别为90分,80分,85分,若依次按50%,30%,20%的比例确定成绩,则该选手的最后得分是__________分.15.当x______时,分式
之间的关系式为__________________.14.为了增强青少年的防毒拒毒意识,学校举办了一次“禁毒教育”演讲比赛,其中某位选手的演讲内容、语言表达、演讲技巧这三项得分分别为90分,80分,85分,若依次按50%,30%,20%的比例确定成绩,则该选手的最后得分是__________分.15.当x______时,分式![]() 有意义.16.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.
有意义.16.如图,正方形ABCD的面积为1,则以相邻两边中点的连线EF为边的正方形EFGH的周长为________.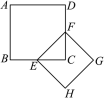 三、解下列各题(本大题共8小题,共72分)17.(8分)化简求值:
三、解下列各题(本大题共8小题,共72分)17.(8分)化简求值:![]() ,从-1,0, 1,2中选一个你认为合适的m值代入求值. 18.(8分)已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.
,从-1,0, 1,2中选一个你认为合适的m值代入求值. 18.(8分)已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.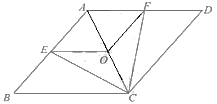 19.(8分)如图,▱ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF
19.(8分)如图,▱ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AF![]() AD.
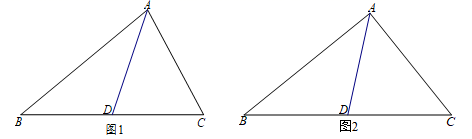
AD.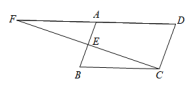 20.(8分)如图1,
20.(8分)如图1,![]() 是
是![]() 的边
的边![]() 上的中线.(1)①用尺规完成作图:延长
上的中线.(1)①用尺规完成作图:延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ;② 若
;② 若![]() ,求
,求![]() 的取值范围;(2)如图2,当
的取值范围;(2)如图2,当![]() 时,求证:
时,求证:![]() .
. 21.(8分)如图1,
21.(8分)如图1,![]() 的
的![]() 所对边分别是
所对边分别是![]() ,且
,且![]() ,若满足
,若满足![]() ,则称
,则称![]() 为奇异三角形,例如等边三角形就是奇异三角形.(1)若
为奇异三角形,例如等边三角形就是奇异三角形.(1)若![]() ,判断
,判断![]() 是否为奇异三角形,并说明理由;(2)若
是否为奇异三角形,并说明理由;(2)若![]() ,
,![]() ,求
,求![]() 的长;(3)如图2,在奇异三角形
的长;(3)如图2,在奇异三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,连结
边上的中点,连结![]() ,
,![]() 将
将![]() 分割成2个三角形,其中
分割成2个三角形,其中![]() 是奇异三角形,
是奇异三角形,![]() 是以
是以![]() 为底的等腰三角形,求
为底的等腰三角形,求![]() 的长.
的长.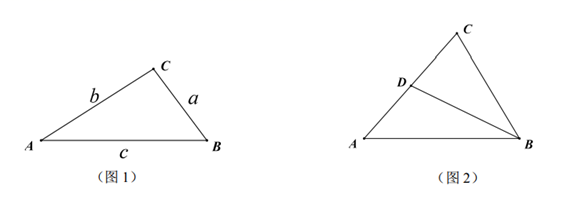 22.(10分)如图,在平面直角坐标系中,直线
22.(10分)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.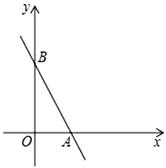 (1)反比例函数
(1)反比例函数![]() 的图象与直线
的图象与直线![]() 交于第一象限内的
交于第一象限内的![]() ,
,![]() 两点
两点![]() ,当
,当![]() 时,求
时,求![]() 的值;(2)设线段
的值;(2)设线段![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,交反比例函数
,交反比例函数![]() 的图象于点
的图象于点![]() ,连接
,连接![]() ,
,![]() ,当以
,当以![]() ,
,![]() ,
,![]() 为顶点的三角形与以
为顶点的三角形与以![]() ,
,![]() ,
,![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 的值. 23.(10分)在平面直角坐标系中,
的值. 23.(10分)在平面直角坐标系中,![]() 的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中
的位置如图所示(每个小方格都是边长为1个单位长度的正方形).其中![]() 、
、![]() 、
、![]() .
.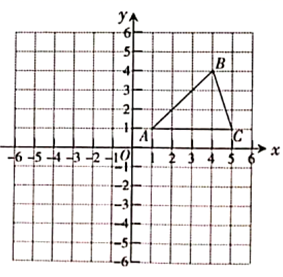 (1)将
(1)将![]() 沿
沿![]() 轴方向向左平移6个单位,画出平移后得到的
轴方向向左平移6个单位,画出平移后得到的![]() ;(2)将
;(2)将![]() 绕着点
绕着点![]() 顺时针旋转90°,画出旋转后得到的
顺时针旋转90°,画出旋转后得到的![]() ,
,![]() 、
、![]() 、的对应点
、的对应点![]() 分别是
分别是![]() 、
、![]() 、
、![]() ; 24.(12分)如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于
; 24.(12分)如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.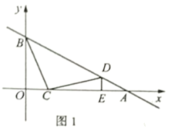 (1)求证,
(1)求证,![]() ;(2)如图2,将
;(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;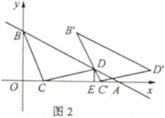 (3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、B4、D5、A6、D7、C8、B9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、2.112、
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、B4、D5、A6、D7、C8、B9、C10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、2.112、![]() 13、
13、![]() 14、115、≠
14、115、≠![]() 16、2
16、2![]() 三、解下列各题(本大题共8小题,共72分)17、
三、解下列各题(本大题共8小题,共72分)17、![]() ,
,![]() 18、(1)证明见解析;(2)AB⊥BC时,四边形AEOF正方形.19、详见解析.20、(1)①详见解析;②1<
18、(1)证明见解析;(2)AB⊥BC时,四边形AEOF正方形.19、详见解析.20、(1)①详见解析;②1<![]() <5;(2)详见解析21、(1)是,理由见解析;(2)
<5;(2)详见解析21、(1)是,理由见解析;(2)![]() ;(3)
;(3)![]() 22、(1)
22、(1)![]() ;(2)
;(2)![]() 或
或![]() .23、(1)的
.23、(1)的![]() 如图所示. 见解析;(2)的
如图所示. 见解析;(2)的![]() 如图所示. 见解析.24、(1)
如图所示. 见解析.24、(1)![]() ,见解析;(2)D(3,1),
,见解析;(2)D(3,1),![]() 平移的距离是
平移的距离是![]() 个单位,见解析;(3)存在满足条件的点Q,其坐标为
个单位,见解析;(3)存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
相关试卷
这是一份浙江省宁波市海曙区2022-2023学年数学七下期末达标检测试题含答案,共6页。
这是一份浙江省杭州下城区五校联考2022-2023学年数学七下期末达标检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列命题中,是假命题的是,下列说法中正确的是,计算等内容,欢迎下载使用。
这是一份浙江省杭州市2022-2023学年数学七下期末达标检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,若,则代数式的值是,如果方程有增根,那么k的值等内容,欢迎下载使用。









