数学必修 第二册6.2 平面向量的运算第2课时教学设计

这是一份数学必修 第二册6.2 平面向量的运算第2课时教学设计，共3页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
6.2.4平面向量的数量积（第二课时）(人教A版普通高中教科书数学必修第二册第六章)一、教学目标掌握平面向量数量积的运算律,能运用运算律解决相关问题.二、教学重难点1.教学重点：掌握平面向量数量积的运算律及常用的公式.2.教学难点：理解平面向量数量积的运算律.三、教学过程【复习引入】回顾：向量a，b的数量积的含义是什么？向量的数量积具有哪些运算性质？  【预设的答案】 a·b＝|a||b|cosθ，其中θ为向量a，b的夹角.设a，b是非零向量，它们的夹角是θ，e是与b方向相同的单位向量，则(1)a·e＝e·a＝|a|cosθ.(2)a⊥b⇔a·b＝0.(3)当a与b同向时，a·b＝|a||b|；当a与b反向时，a·b＝－|a||b|，特别地，a·a＝|a|2或|a|＝.　.(4)|a·b|≤|a|·|b|.【设计意图】复习回顾向量数量积第一课时的主要内容，为第二课时的学习做好准备.1.呈现背景，提出问题探究：类比数的乘法运算律，结合向量的线性运算律，你能得到数量积的哪些运算律？【活动预设】展示数学乘法运算的运算律，及前两节所学的向量的线性运算律，学生类比出数量积的一些运算律.【预设的答案】  运算律实数乘法向量数量积判断正误交换律ab＝baa·b＝b·a正确结合律(ab)c＝a(bc)(λa)·b=λ(a·b)＝a·(λb)a(b·c)＝(a·b)c正确错误分配律(a＋b)c＝ac＋bc(a＋b)·c＝a·c＋b·c正确 【设计意图】引导学生类比已学内容，做出猜想，为引入本节的数量积运算律做铺垫.2.分析联想，寻求方法活动：尝试说明上述猜想正确与否，并给出证明：（1）a·b＝b·a；  （2）(λa)·b=λ(a·b)＝a·(λb)； a(b·c)＝(a·b)c    （3）(a＋b)·c＝a·c＋b·c.【活动预设】教师带领学生讨论，学生尝试说明以上猜想正确与否.【预设的答案】（1）交换律显然成立.（2）数乘结合律：(λa)·b=λ(a·b)＝a·(λb)(λa)·b=|λa||b|cos θ1    λ(a·b)=λ|a||b|cos θ2     a·(λb)=|a||λb|cos θ3 对λ分类讨论可以说明数乘结合律是成立的. 数量积结合律： 思考： a(b·c)＝(a·b)c成立吗？由于 a(b·c)表示与a共线的向量，(a·b)c表示与c共线的向量，所以这个式子不成立.（3）分配律：(a＋b)·c＝a·c＋b·c教师讲授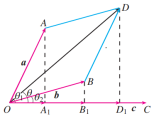：利用a＋b的投影向量等于a与b的投影向量之和可以证明.【设计意图】培养学生的归纳总结能力；鼓励学生大胆猜想，小心求证；紧扣向量的数量积定义进行运算律的验证，便于理解向量数量积的运算律.3.猜想验证，得出结论向量数量积的运算律：（1）a·b＝b·a；（交换律）  （2）(λa)·b=λ(a·b)＝a·(λb)；（数乘结合律）（3）(a＋b)·c＝a·c＋b·c.（分配律）例1：我们知道，对于任意的，恒有对于任意向量a，b,是否也有下面类似的结论？(a＋b)·a＝(a+b)2=a2+2a·b＋b2      (a＋b)·(a－b)=a2－b2【活动预设】学生可利用分配律和交换律自行推导，加深对数量积运算律的理解.【设计意图】通过数量积运算律的探索过程，学生已感受到类比推理的魅力.进一步类比实数范围内常用的结论，可以得到向量范围内的常用结论.4.运用新知，巩固内化例2：已知|a|＝6，|b|＝4，a，b的夹角是，求(a＋2b)·(a－3b).【活动预设】学生动手操作，尝试初步运用. 【设计意图】应用向量运算律解决计算问题，对初学者来说是有些难度的，教师根据运算律详细展示计算过程，加深巩固学生对新知识的把握.例3：已知|a|＝3，|b|＝4，且a，b不共线. 当k为何值时，向量a＋kb与a－kb互相垂直？【活动预设】引导学生开动脑筋，考虑将几何问题与向量联系起来.【设计意图】通过此题让学生感受向量处理问题的优势. 通过向量运算将几何问题转化为代数问题，这为解决几何问题提供了新的思路.5.回顾反思，拓展问题问题1. 向量的数量积运算律是怎样的？问题2. 类比实数中的结论，数量积是否有相似的结论呢？比如a·b＝b·c(b≠0)⇒a＝c（消去律）等是否也成立呢？【设计意图】（1）回顾总结本节的主要内容，加深印象；（2）突出本节课类比推理，将未知化已知的思想方法，给学生留下想象的空间，让学生自  主探索，激发兴趣，获得成就感.