2022-2023学年四川营山小桥中学数学七下期末质量跟踪监视模拟试题含答案

这是一份2022-2023学年四川营山小桥中学数学七下期末质量跟踪监视模拟试题含答案，共6页。
2022-2023学年四川营山小桥中学数学七下期末质量跟踪监视模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．下列角度中，不能是某多边形内角和的是（    ）A．600° B．720° C．900° D．1080°2．某老师为了解学生周末学习时间的情况，在所任班级中随机调查了10名学生，绘成如图所示的条形统计图，则这10名学生周末学均时间是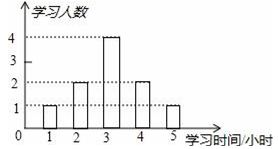（ ）A．4 B．3 C．2 D．13．若点A(–2，)、B( –1，)、C(1，)都在反比例函数(为常数)的图像上，则、、的大小关系为（    ）A． B． C． D．4．一家鞋店在一段时间内销售了某种女鞋30双，各种尺码的销售量如下表所示，你认为商家更应该关注鞋子尺码的（  ）尺码/cm
 22
 22.5
 23
 23.5
 24
 24.5
 25
 销售量/双
 4
 6
 6
 10
 2
 1
 1
 A．平均数 B．中位数 C．众数 D．方差5．下列等式成立的是（　　）A． B． C． D．6．已知一次函数y＝x﹣1的图象经过点（1，m），则m的值为（　　）A． B．1 C．－ D．﹣17．已知a＞b，若c是任意实数，则下列不等式中总是成立的是（）A．a-c＞b-c B．a+c＜b+c C．ac＞bc D．ac＜bc8．下列由左到右的变形，属于因式分解的是（    ）A． B．C． D．9．已知下列命题：①若a＞0，b＞0，则a+b＞0；②若a2＝b2，则a＝b；③角的平分线上的点到角的两边的距离相等；④矩形的对角线相等．以上命题为真命题的个数是（　　）A．1个 B．2个 C．3个 D．4个10．某校为了了解学生在校午餐所需的时间，抽查了 20 名同学在校午餐所需的时间，获得如 下数据（单位：分）：10，12，15，10，1，18，19，18，20，34，22，25，20，18，18，20，15，1，21，1．若将这些数据分为 5组，则组距是（    ）A．4 分 B．5 分 C．6 分 D．7 分11．某居民小区10户家庭5月份的用水情况统计结果如表所示：这10户家庭的月平均用水量是(   )月用水量/m345689户数23311A．2m3                                    B．3.2m3                                    C．5.8m3                                D．6.4m312．如图，在周长为20cm的平行四边形ABCD中，AB≠AD，AC和BD相交于点O，OE⊥BD交AD于E，则ΔABE的周长为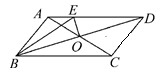（    ）A．4cm B．6cm C．8cm D．10cm二、填空题（每题4分，满分20分，将答案填在答题纸上）13．如图，在坐标系中，有，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知是由旋转得到的．请写出旋转中心的坐标是____，旋转角是____度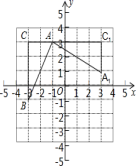．14．在平行四边形ABCD中，，则的度数是______°．15．一组数据：的方差是__________．16．为选派诗词大会比赛选手，经过三轮初赛，甲、乙、丙、丁四位选手的平均成绩都是86分，方差分别是s甲2=1.5，s乙2=2.6，s丙2=3.5，s丁2=3.68，若要从中选一位发挥稳定的选手参加决赛你认为派__________________去参赛更合适（填“甲”或“乙”或“丙”或“丁”）17．将一个矩形纸片沿折叠成如图所示的图形，若，则的度数为________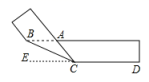． 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）如图，矩形中，对角线的垂直平分线与相交于点，与相交于点，连接，．求证：四边形是菱形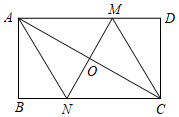．   19．（5分）已知一次函数的图象经过，两点．（1）求这个一次函数的解析式；（2）试判断点是否在这个一次函数的图象上；（3）求此函数图象与轴，轴围成的三角形的面积．   20．（8分）如图，在菱形ABCD中，AC，BD相交于点O，E为AB的中点，DE⊥AB．（1）求∠ABC的度数；（2）如果AC＝4，求DE的长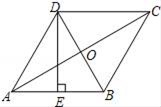．   21．（10分）某大型物件快递公司送货员每月的工资由底薪加计件工资两部分组成，计件工资与送货件数成正比例．有甲乙两名送货员，如果送货量为x件时，甲的工资是y1（元），乙的工资是y2（元），如图所示，已知甲的每月底薪是800元，每送一件货物，甲所得的工资比乙高2元（1）根据图中信息，分别求出y1和y2关于x的函数解析式；（不必写定义域）（2）如果甲、乙两人平均每天送货量分别是12件和14件，求两人的月工资分别是多少元？（一个月为30天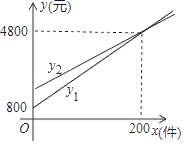）   22．（10分）某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处错误．回答下列问题：（1）写出条形图中存在的错误，并说明理由； （2）写出这20名学生每人植树量的众数、中位数； （3）在求这20名学生每人植树量的平均数时，小宇是这样分析的：① 小宇的分析是从哪一步开始出现错误的？ ② 请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵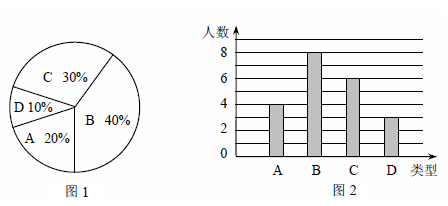．   23．（12分）传统节日“春节”到来之际，某商店老板以每件60元的价格购进一批商品，若以单价80元销售，每月可售出300件.调查表明：单价每上涨1元，该商品每月的销售量就减少10件．（1）请写出每月销售该商品的利润y（元）与单价x（元）间的函数关系式；（2）单价定为多少元时，每月销售商品的利润最大？最大利润为多少？   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、A2、B3、C4、C5、D6、C7、A8、D9、C10、B11、C12、D 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、    1    14、100°15、.16、甲17、126° 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、见解析19、（1）；（2）不在这个一次函数的图象上；（3）函数图象与轴，轴围成的三角形的面积=4.20、（1）；（2）．21、（1）y1＝20x+800；y2＝18x+1200；（2）y1＝8000元；y2＝8760元．22、解：（1）D错误（2）众数为1，中位数为1．（2）①小宇的分析是从第二步开始出现错误的．②1278（颗）23、（1）y=-10x2+100x+6000（0≤x≤30）；（2） 单价定为5元时，每月销售商品的利润最大，最大利润为6250元.