数学21.1 二次函数完整版ppt课件

这是一份数学21.1 二次函数完整版ppt课件，共35页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，当x8时则，所以此球不能投中，1跳得高一点儿，解根据题意得，解方程组得，解方程得，何时橙子总产量最大等内容，欢迎下载使用。

1.掌握如何将实际问题转化为数学问题；（重点）2.进一步理解二次函数在解决实际问题中的应用；（重点）3.进一步体会数形结合的数学思想方法.（难点）
行驶中的汽车，在制动后由于惯性，还要继续向前滑行一段距离才能停止，在此运动中存在着许多与数学知识有关的实际问题.那么何时急刹车，才能避免追尾呢？
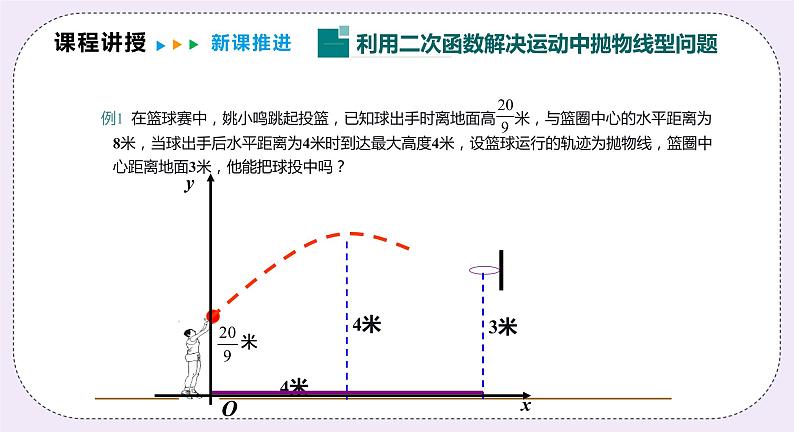
例1 在篮球赛中，姚小鸣跳起投篮，已知球出手时离地面高 米，与篮圈中心的水平距离为8米，当球出手后水平距离为4米时到达最大高度4米，设篮球运行的轨迹为抛物线，篮圈中心距离地面3米，他能把球投中吗？
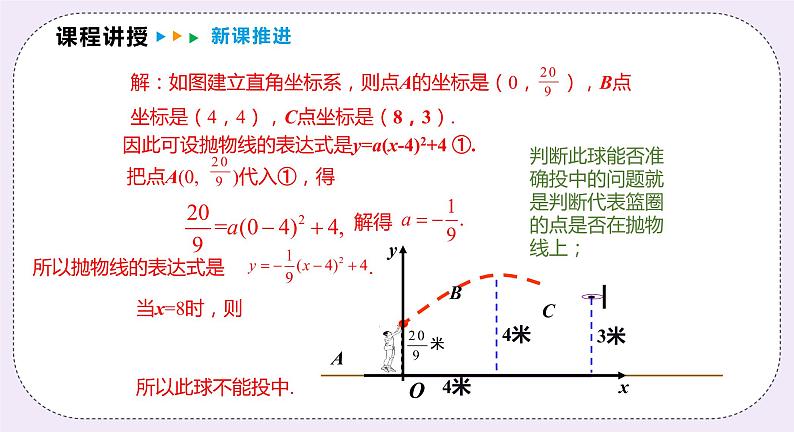
因此可设抛物线的表达式是y=a(x-4)2+4 ①.
所以抛物线的表达式是 .
判断此球能否准确投中的问题就是判断代表篮圈的点是否在抛物线上；
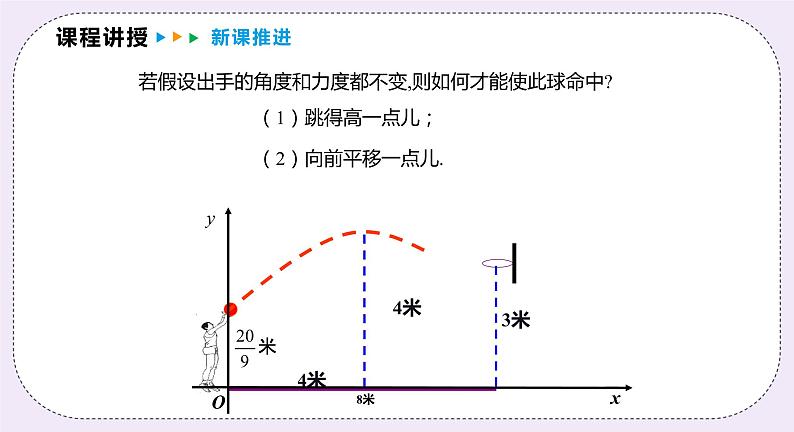
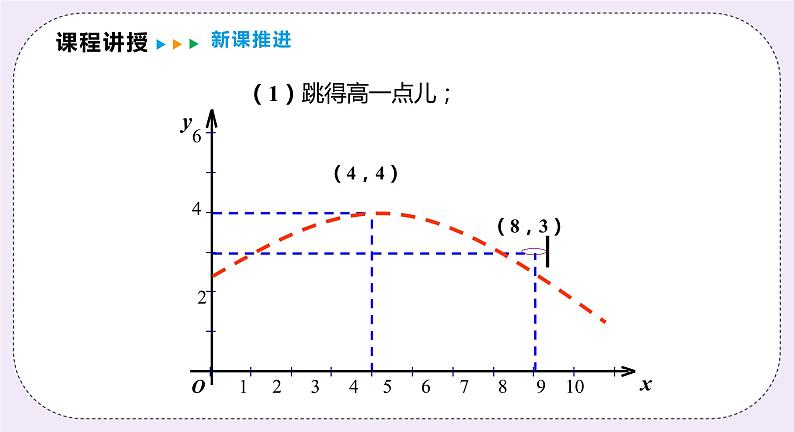
若假设出手的角度和力度都不变,则如何才能使此球命中?
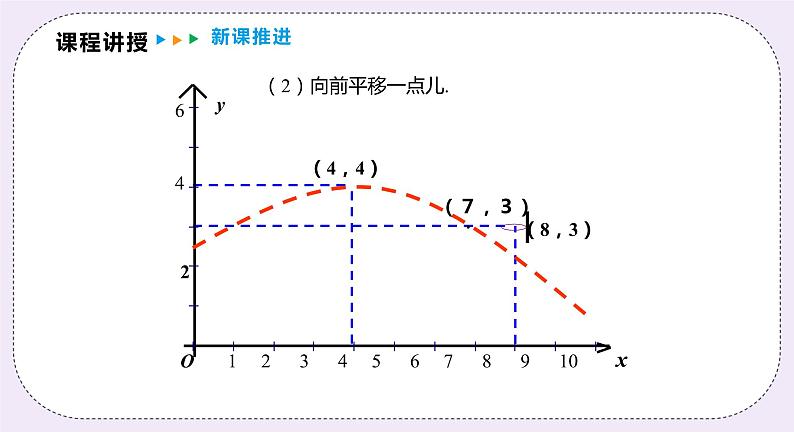
（2）向前平移一点儿.
O 1 2 3 4 5 6 7 8 9 10
O 1 2 3 4 5 6 7 8 9 10
（７，３） ●
例2 上抛物体在不计空气阻力的情况下，有如下表达式：其中h是物体上升的高度，v0是物体被上抛时竖直向上的初始速度，g是重力加速度(取g=10m/s2)， t是物体抛出后经过的时间. 在一次排球比赛中，排球从靠近地面处被垫起时竖直向上的初始速度为10m/s.(1)问排球上升的最大高度是多少？
因为抛物线开口向下，顶点坐标为（1，5）. 即排球上升的最大高度为5m.
(2) 已知某运动员在2.5m高度时扣球效果最佳，如果她要打快攻，问该运动员在排球被垫起后多长时间扣球最佳？
排球在上升和下落中，各有一次经过2.5m高度，但第一次经过时离排球被垫起仅有0.3s，要打快攻，选择此时扣球，可令对方措手不及，易获成功.
解：当h=2.5 m时，得
如果来不及在0.3s扣球，她还可在何时扣球？
例3 跳绳时，绳甩到最高处时的形状是抛物线．已知正在甩绳的甲、乙两名同学拿绳的手间距AB为6米，手到地面的距离AO和BD均为0.9米，身高为1.4米的小丽站在距点O水平距离为1米的点F处，绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系，设此抛物线对应的函数表达式为y＝ax2＋bx＋0.9.(1)求该抛物线对应的函数表达式；(2)如果小刚站在OD之间，且离点O的距离为3米，当绳子甩到最高处时恰好通过他的头顶，请你计算出小刚的身高；(3)如果身高为1.4米的小丽站在OD之间，且离点O的距离为t米，绳子甩到最高处时超过她的头顶，请写出t的取值范围．
解析：对于第(1)问，由题意可知E点的坐标为(1，1.4)，B点的坐标为(6，0.9)，将这两点的坐标代入y＝ax2＋bx＋0.9，可以求出抛物线对应的函数表达式；对于第(2)问，实质是求当x＝3时的函数值；对于第(3)问，结合图象并根据轴对称性求t的取值范围．
∴所求抛物线对应的函数表达式是y＝－0.1x2＋0.6x＋0.9.
解：(1)由题意得点E(1，1.4)，B(6，0.9)在抛物线上，将它们代入y＝ax2＋bx＋0.9，得
(1)求该抛物线对应的函数表达式；
解：当x＝3时，y＝－0.1×32＋0.6×3＋0.9＝1.8， ∴小刚的身高是1.8米.
(2)如果小刚站在OD之间，且离点O的距离为3米，当绳子甩到最高处时恰好通过他的头顶，请你计算出小刚的身高；
解：由抛物线的轴对称性可知1(3)如果身高为1.4米的小丽站在OD之间，且离点O的距离为t米，绳子甩到最高处时超过他的头顶，请写出t的取值范围．
2.根据建立好的坐标系求出该函数的表达式；3.在实际问题中要注意自变量的取值范围内.
1.首先要建立适当的平面直角坐标系；
求解运动中的抛物线问题一般步骤
例4 行驶中的汽车，在制动后由于惯性，还要继续向前滑行一段距离才能停止，这段距离称为“制动距离”.为了了解某型号汽车的制动性能，对其进行了测试，测得数据如下表：
有一辆该型号汽车在公路上发生了交通事故，现场测得制动距离为46.5m，试问交通事故发生时车速是多少？是否因超速（该段公路限速为110km/m）行驶导致了交通事故？
制动时车速/km•h-1
【分析】 要解答这个问题，就是要解决在知道了制动距离时，如何求得相应的制动时车速.题中给出了几组制动距离与制动时车速之间的关联数据，为此，求出制动距离与制动时车速的函数表达式是解答本题的关键.
解： 以制动时车速的数据为横坐标（x值）、制动距离的数据为纵坐标（y值），在平面直角坐标系中，描出各组数据对应的点，如图.
观察图中描出的这些点的整体分步，它们基本上都是在一条抛物线附近，因此，y与x之间的关系可以近似地以二次函数来模拟，即设 y=ax²+bx+c
任选三组数据，代入函数表达式，得
即所求二次函数表达式为 y=0.002x²+0.01x（x≥0）.
把y=46.5m代入上式，得
答：制动时车速为150km/h(＞110km/h)，即在事故发生时，该汽车属超速行驶.
46.5=0.002x²+0.01x
x1=150（km/h）, x2=-155（km/h）(舍去）.
(1)问题中有哪些变量？其中哪些是自变量？哪些是因变量？
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树？这时平均每棵树结多少个橙子？
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
例5 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1) 变量有果园橙子的总产量，果园里增种的橙子树的棵树，自变量是果园增种的橙子数的棵树，因变量是果园橙子的总产量；
（2）果园共有（100+x）棵树,平均每棵树结（600-5x）个橙子；
思考：某商品现在的售价为每件60元，每星期可卖出300件，已知商品的进价为每件40元，则每星期销售额是 元，销售利润 元.
（1）销售额= 售价×销售量;
（2）利润= 销售额-总成本=单件利润×销售量;
（3）单件利润=售价-进价.
设未知数(确定自变量和函数);找等量关系,列出函数关系式;化简,整理成标准形式(一次函数、二次函数等);求自变量取值范围；利用函数知识，求解（通常是最值问题）；写出结论.
某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出18件，已知商品的进价为每件40元，如何定价才能使利润最大？
（1）涨价销售①每件涨价x元，则每星期售出商品的利润y元，填空：
y=(20+x)(300-10x)
建立函数关系式 y=(20+x)(300-10x),
即 y=-10x2+100x+6000.
（2）降价销售①每件降价x元，则每星期售出商品的利润y元，填空：
建立函数关系式 y=(20-x)(300+18x)，
即 y=-18x2+60x+6000.
某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价1元，每星期少卖出10件；每降价1元，每星期可多卖出18件，已知商品的进价为每件40元，如何定价才能使利润最大？
y=(20-x)(300+18x)
②自变量x的取值范围如何确定？
营销规律是价格下降，销量上升，因此只要考虑单件利润就可以，故20-x ≥0，且x ≥0,因此自变量的取值范围是0 ≤ x ≤20.
③降价多少元时，利润最大，是多少？
习题2 某网络玩具店引进一批进价为20元/件的玩具，如果以单价30元出售，那么一个月内售出180件，根据销售经验，提高销售单价会导致销售量的下降，即销售单价每上涨1元，月销售量将相应减少10件，当销售单价为多少元时，该店能在一个月内获得最大利润？
①每件商品的销售单价上涨x元，一个月内获取的商品总利润为y元，填空：
y=(10+x)(180-10x)
建立函数关系式 y=(10+x)(180-10x),
即 y=-10x2+80x+1800.
营销规律是价格上涨，销量下降，因此只要考虑销售量就可以，故180-10x ≥0，因此自变量的取值范围是x ≤18.
③涨价多少元时，利润最大，最大利润是多少？
习题3 某化工材料经销公司购进了一种化工原料共7000千克，购进价格为每千克30元.物价部门规定其销售单价不得高于每千克70元，也不得低于30元.市场调查发现：单价定为70元时，日均销售60千克；单价每降低1元，日均多售出2千克.在销售过程中，每天还要支出其它费用500元（天数不足一天时，按整天计算）.设销售单价为x元，日均获利为y元.（1）求y关于x的函数关系式，并注明x的取值范围；（2）将上面所求出的函数配方成顶点式，写出顶点坐标， 并指出单价定为多少元时日均获利最多，是多少？
【分析】（1）日利润=每千克的利润×日销售量﹣杂支，根据物价部门规定，x的取值范围是30≤x≤70；（2）用配方法变形，根据对称性画草图解答．                                           
求解最大利润问题的一般步骤
（1）建立利润与价格之间的函数关系式：运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
（2）结合实际意义，确定自变量的取值范围；
（3）在自变量的取值范围内确定最大利润：可以利用配方法或公式求出最大利润；也可以画出函数的简图，利用简图和性质求出.