

高中数学北师大版 (2019)必修 第二册1.1 构成空间几何体的基本元素导学案及答案
展开第五章 立体几何初步
5.1 基本立体图形
新课程标准 | 学业水平要求 |
1.了解构成空间几何体的基本元素. 2.利用实物、计算机软件等观察空间图形,认识棱柱、棱锥、棱台的结构特征. 3.能运用这些特征描述现实生活中简单物体的结构. | 1.结合身边的实例了解构成空间几何体的基本元素.(直观想象) 2.结合身边的实物模型,认识棱柱、棱锥、棱台的结构特征.(数学抽象) 3.理解棱柱、棱锥、棱台的定义,知道棱柱、棱锥、棱台的结构特征,并能识别.(直观想象) 4.能将棱柱、棱锥、棱台的表面展开成平面图形,并解决相关问题.(直观想象、逻辑推理) |
5.1.1 构成空间几何体的基本元素
课前篇·自主学习预案 |
1.构成空间几何体的基本元素
(1)构成空间几何体的基本元素
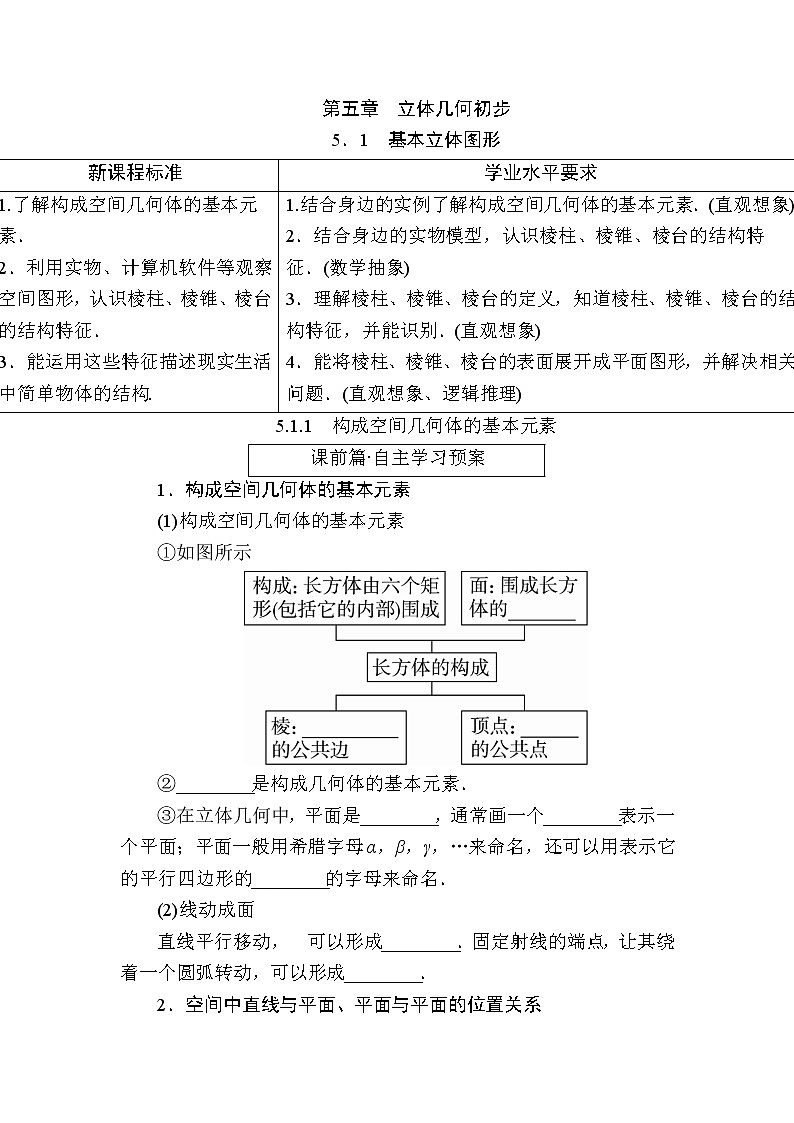
①如图所示
②________是构成几何体的基本元素.
③在立体几何中,平面是________,通常画一个________表示一个平面;平面一般用希腊字母α,β,γ,…来命名,还可以用表示它的平行四边形的________的字母来命名.
(2)线动成面
直线平行移动, 可以形成________.固定射线的端点,让其绕着一个圆弧转动,可以形成________.
2.空间中直线与平面、平面与平面的位置关系
(1)空间中直线与平面的关系
①直线与平面平行:直线与平面________公共点.
②直线与平面相交:直线与平面有且仅有________公共点.
(2)空间中平面与平面的位置关系
①两个平面相交:两个平面有一条公共直线.
特别地,如果两个平面相交,并且其中一个平面通过一个平面的一条垂线,我们说这两个平面________.
②两个平面平行:两个平面________公共点.
答案:1.(1)①各个矩形 相邻两个面 棱和棱 ②点、线、面 ③无限延展的 平行四边形 对角顶点
(2)平面或曲面 锥面
2.(1)①没有 ②一个
(2)①垂直 ②没有
课堂篇·研习讨论导案 |
研习1 平面概念的理解
[典例1] 下列命题:
①书桌面是平面;
② 8个平面重叠起来,要比2个平面重叠起来厚;
③一个平面的长是20 cm,宽是10 cm;
④平面是绝对的平、无厚度,可以无限延展的抽象的数学概念.
其中错误命题的是( )
A.① B.②
C.③ D.④
[自主记]
[分析] 根据平面的概念判断.
[答案] ABC
[解析] 平面有无限延伸性,故①错,③错,平面是一个抽象的概念,没有厚度,故②错误.
[巧归纳] 立体几何中的平面与平面几何中的平面图形是有区别的.平面图形如三角形、正方形、梯形等是有大小之分的;而立体几何中所说的平面是无大小、厚薄之分的,它类似于以前我们学过的直线,它可以无限延伸,它是不可度量的.
[练习1] 判断下列说法是否正确?并说明理由.
(1)平行四边形是一个平面;
(2)任何一个平面图形都是一个平面;
(3)空间图形中先画的线是实线,后画的线是虚线.
解:(1)不正确.平行四边形是平面上四条线段构成的图形,它是不能无限延展的.
(2)不正确.平面和平面图形是完全不同的两个概念,平面图形是有大小的,它是不能无限延展的.
(3)不正确.在空间图形中,为了增强图形的立体感,都是把能够看得见的线画成实线,把被平面遮住的线画成虚线(无论是图形中原有的,还是后来引入的辅助线).
研习2 构成几何体的基本元素
[典例2] (1)(多项选择题)下列属于构成几何体的基本元素的是( )
A.点 B.线段
C.曲面 D.多边形(不含内部的点)
(2)如图所示,请画出①②③中线段AB绕着直线l旋转一周形成的空间图形?
[自主记]
(1)[答案] ABC
[解析] 空间几何体的基本元素是点、线、面,而非多边形.
(2)[分析] 线的运动可以形成平面或曲面,观察AB和l的位置关系及旋转的方式和方向,可以尝试画出形成的图形.
[解] 如图所示.
[巧归纳] 1.点、线、面是构成几何体的基本元素,任何一个几何体都是由这些基本元素组成的,而其他图形有时也能构成另外复杂的几何体,但是不能称之为“基本元素”.
2.点、线、面运动形成怎样的图形与其运动的形式和方向有关,如果直线与旋转轴平行,那么形成圆柱面,如果与旋转轴斜交,那么形成圆锥面.
3.在判断点、线、面按一定规律运动形成的几何体的形状时,可以借助身边的实物来模拟.
[练习2] 以下结论中不正确的是( )
A.平面上一定有直线
B.平面上一定有曲线
C.曲面上一定无直线
D.曲面上一定有曲线
答案:C
研习3 长方体中基本元素间的位置关系
[典例3] 如图所示,在长方体ABCD-A′B′C′D′中,如果把它的12条棱延伸为直线,6个面延伸为平面,那么在这12条直线与6个平面中,回答下列问题:
(1)与直线B′C′平行的平面有哪几个?
(2)与直线B′C′垂直的平面有哪几个?
(3)与平面BC′平行的平面有哪几个?
(4)与平面BC′垂直的平面有哪几个?
[自主记]
[分析] 细心观察图形,判定与B′C′平行、垂直的平面、与面BC′平行、垂直的平面.
[解] (1)与直线B′C′平行的平面有:平面AD′,平面AC.
(2)与直线B′C′垂直的平面有:平面AB′,平面CD′.
(3)与平面BC′平行的平面有:平面AD′.
(4)与平面BC′垂直的平面有:平面AB′,平面A′C′,平面CD′,平面AC.
[巧归纳] 1.解决此类问题的关键在于识图,根据图形识别直线与平面平行、垂直,平面与平面平行、垂直.
2.长方体和正方体是立体几何中的重要几何体,对其认识有助于进一步认识立体几何中的点、线、面的基本关系.
[练习3] 下列关于长方体的叙述不正确的是( )
A.将一个矩形沿竖直方向平移一段距离可形成一个长方体
B.长方体中相对的面都互相平行
C.长方体中某一底面上的高的长度就是两平行底面间的距离
D.两底面之间的棱互相平行且相等
答案:A
达标篇·课堂速测演习
1.下列结论正确的个数有( )
①曲面上可以存在直线;
②平面上可以存在曲线;
③曲线运动的轨迹可形成平面;
④直线运动的轨迹可形成曲面;
⑤曲面上不能画出直线.
A.3个 B.4个
C.5个 D.2个
答案:B
2.下列关于长方体的说法中,正确的是________.(填写正确命题的序号).
①长方体有六个面;
②长方体的顶点的个数小于长方体的棱的条数;
③将一个水平放置的矩形ABCD(包括其内部)各点沿一定方向移动相同的距离得到矩形A′B′C′D′,所形成的几何体是长方体.
答案:①②
解析:由长方体的有关概念知①②正确;③中当把矩形ABCD(包括其内部)各点沿竖直方向移动相同的距离时,形成的几何体才是长方体,故③是错误的.
3.线段AB长为5 cm,在水平面上向右移动4 cm后记为CD,将CD沿铅垂线方向向下移动3 cm后记为C′D′,再将C′D′沿水平方向向左移动4 cm后记为A′B′,依次连接构成长方体ABCD-A′B′C′D′.
(1)该长方体的高为________;
(2)平面A′B′BA与平面CDD′C′间的距离为________;
(3)点A到平面BCC′B′的距离为________.
答案:(1)3 cm (2)4 cm (3)5 cm
解析:如图,在长方体ABCD-A′B′C′D′中,AB=5 cm,BC=4 cm,CC′=3 cm,∴长方体的高为3 cm;平面A′B′BA与平面CDD′C′之间的距离为4 cm;点A到平面BCC′B′的距离为5 cm.
4.试指出图中各几何体是由哪些基本元素组成的.
解:①中几何体由6个顶点、12条棱和8个面组成;②中几何体由12个顶点、18条棱和8个面组成;③中几何体由6个顶点、10条棱和6个面组成.
[误区警示] 忽视几何中的线线、线面关系致误
[典例] 下列关于长方体的说法中,正确的是________.
①长方体中有3组对面互相平行:
②在长方体ABCD-A1B1C1D1中,与AB垂直的只有棱AD,BC和AA1;
③长方体可看成是由一个矩形平移形成的;
④长方体ABCD-A1B1C1D1中,棱AA1,BB1,CC1,DD1平行且相等.
[错误解答] 根据长方体中六个面,十二条棱间的相互关系可以判断①②③④都正确.
[错误原因分析] 在对长方体ABCD-A1B1C1D1中的棱AB进行分析时,由于长方体中的棱比较多,忽视了另外的五条棱B1C1,A1D1,BB1,CC1和DD1也与AB是垂直关系.
[正解] 如图,在长方体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,平面ADD1A1∥平面BCC1B1,
平面ABB1A1∥平面CDD1C1,故①正确;与AB垂直的棱除了AD,BC,AA1外,还有B1C1,A1D1,BB1,CC1和DD1,故②错误;
这个长方体可看成由它的一个面ABCD上各点沿竖直方向向上移动相同距离AA1所形成的几何体,故③正确;棱AA1, BB1,CC1,DD1的长度是长方体中面ABCD和面A1B1C1D1的距离,因此它们平行且相等,故答案是①③④.
[答案] ①③④
[防范措施] 在研究空间几何中点线面的位置关系时,由于几何体中的点线面比较多,一定要养成认真分析、仔细观察的习惯,特别是画出图形分析对正确解题更为必要.
北师大版 (2019)必修 第二册4.1 平面向量基本定理学案: 这是一份北师大版 (2019)必修 第二册4.1 平面向量基本定理学案,共8页。
高中人教B版 (2019)6.2.1 向量基本定理导学案: 这是一份高中人教B版 (2019)6.2.1 向量基本定理导学案,共10页。
高中数学北师大版 (2019)必修 第二册1.1 构成空间几何体的基本元素学案: 这是一份高中数学北师大版 (2019)必修 第二册1.1 构成空间几何体的基本元素学案,共11页。













